HDU 5114 Collision（扩展欧几里得） xgtao

Collision

给出l*w的球桌，再给出球桌上的两个球（x1,y1）(x2,y2)，分别以（1,1）的速度进行运动，问他们第一次碰撞的坐标。

首先将速度进行正交分解，分解成沿水平的方向1和沿竖直的方向1：

第一种情况：

第二种情况：

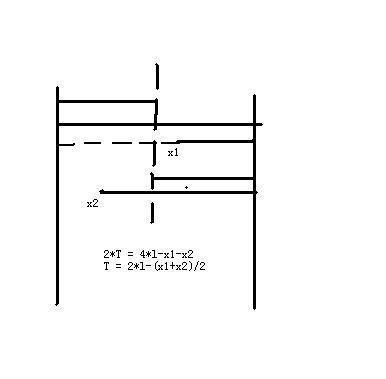
T = 2*l-(x1+x2)/2+2nl;

T = l-(x1+x2)/2+2nl;

合并得到：T = nl-(x1+x2)/2;

同理得到：T = n'w-(y1+y2)/2;

然后nl-n'w = (x1+x2)/2-(y1+y2)/2,由扩展欧几里得解出n,n',求出n最小解然后解出T,然后坐标+T mod 2*l,如果坐标>l,就用2*l-l,就求出x,y;

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#define eps 1e-6
#define LL long long
using namespace std;

//T = k1l-(x1+x2)/2
//T = k2w-(y1+y2)/2
//lk1-wk2 = (x1+x2)/2-(y1+y2)/2

void exgcd(LL a,LL b,LL &gcd,LL &x,LL &y){
	if(!b){gcd = a;x = 1;y = 0;}
	else{exgcd(b,a%b,gcd,y,x);y -= x*(a/b);}
}

double ansx,ansy,tt;
int r,kase,l,w,x,y,xx,yy;
LL gcd,k1,k2;

int main(){
	scanf("%d",&r);
	for(int kase = 1;kase <= r;++kase){
		printf("Case #%d:\n",kase);
		scanf("%d%d",&l,&w);
		scanf("%d%d%d%d",&x,&y,&xx,&yy);
		if(x == xx && y == yy){printf("%.1lf %.1lf\n",1.0*x,1.0*y);continue;}
		if(x == xx){
			tt = w-1.0*(y+yy)/2.0;
			ansy = y+tt>w?2*w-y-tt:y+tt;
			ansx = x+tt>l?2*l-x-tt:x+tt;
			printf("%.1lf %.1lf\n",ansx,ansy);
			continue;
		}
		if(y == yy){
			tt = l-1.0*(x+xx)/2.0;
			ansx = x+tt>l?2*l-x-tt:x+tt;
			ansy = y+tt>w?2*w-y-tt:y+tt;
			printf("%.1lf %.1lf\n",ansx,ansy);
			continue;
		}
		LL p = x+xx-y-yy;
		if(p%2 != 0){puts("Collision will not happen.");continue;}
		p >>= 1;
		LL a = l,b = -w;
		exgcd(a,b,gcd,k1,k2);
		if(p%gcd != 0){puts("Collision will not happen.");continue;}
		
		k1 = p/gcd*k1;
		LL z = k1/(w/gcd);
		k1 -= w/gcd*z;  
        if(k1<1) k1 += abs(w/gcd); //最小正整数解 
        
		tt = k1*l-1.0*(xx+x)/2.0;
		LL c = (x+tt)/(2*l+eps);
		double tx = x+tt-2.0*l*c;
		c = (y+tt)/(2*w+eps);
		double ty = y+tt-2.0*c*w;
		ansx = tx>l?2*l-tx:tx;
		ansy = ty>w?2*w-ty:ty;
		printf("%.1lf %.1lf\n",ansx,ansy);
	}
	return 0;
}