1.1 SAT
SAT. Given a CNF formula Φ, does it have a satisfying truth assignment?
可满足性要求的是结果为TRUE!
1.1.1 3-SAT
SAT: where each clause contains exactly 3 literals
(and each literal corresponds to a different variable).
先来看一个列子:
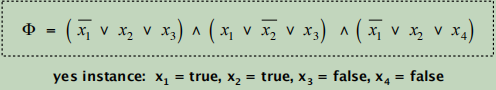
当然一个正确的实例是非常好找到的!(那么有没有可能永远找不到解?)答案是肯定!原因见下文。
科学界一直存在的一个问题就是3元可满足性问题有没有多项式时间算法解!
1.1.2 3-satisfiability reduces to independent set
Pf. Given an instance Φ of 3-SAT, we construct an instance (G, k) of
INDEPENDENT-SET that has an independent set of size k = ⎜Φ⎜ iff Φ is satisfiable.
定理:3元可满足性问题可以规约到独立集问题。
Construction.
- G contains 3 nodes for each clause, one for each literal.
- Connect 3 literals in a clause in a triangle.
- Connect literal to each of its negations
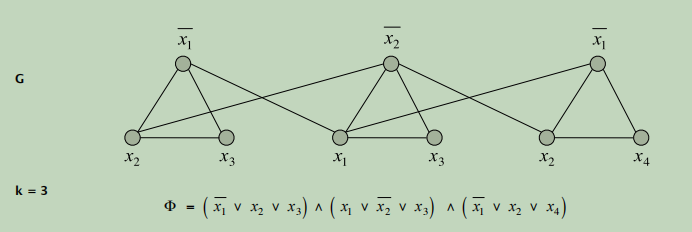
构造方法是这样的把图G分为三个模块每一个模块由三个顶点构成,每一个模块中的三条边对应文法式中的一个子文法,三个模块之间的连接点由文法式中有“非”运算的对等结点。
1.1.3 必要性
定理:Φ is satisfiable iff G contains an independent set of size k = ⎜Φ⎜.
Pf.
⇐ Consider any satisfying assignment for Φ.
- Select one true literal from each clause/triangle.
- This is an independent set of size k = ⎜Φ⎜.
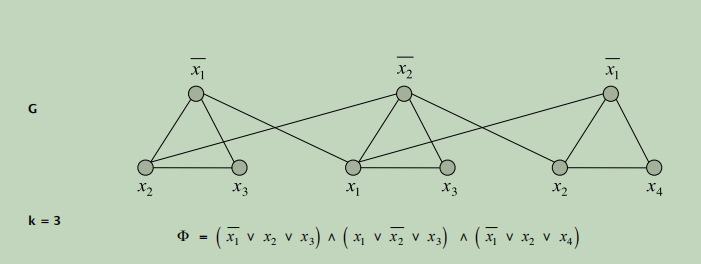
考虑任意一种3元可满足性解,就拿一个实例x1=true,x2=true,x3=true,x4=true.
在图G中标记出值为True的结点,很显然这些结点不能构成独立集!
结论:“no” instances of 3-SAT are solved correctly!
1.1.4 充分性
定理:Φ is satisfiable iff G contains an independent set of size k = ⎜Φ⎜.
Pf. ⇒ Let S be independent set of size k.
- S must contain exactly one node in each triangle.
- Set these literals to true (and remaining literals consistently).
- All clauses in Φ are satisfied.
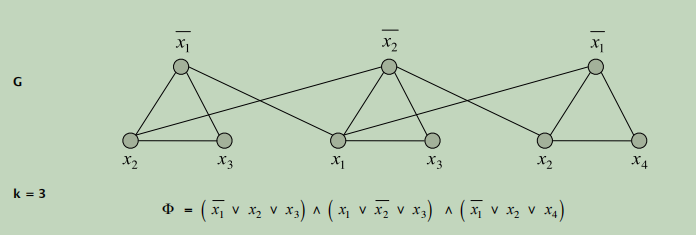
如果S独立集的大小为k,那么S必然在每一个小三角形模块中包含一个结点。比如我们选每个三角形最上面的结点,按照规定这三个结点的值为TRUE。
那么对应的文法式有x1=false,x2=false,x3=?,x4=?,x3,x4任意取值。显然文法式成立!
结论:yes” instances of 3-SAT are solved correctly!