Theorem. PLANAR-3-COLOR ≣ P PLANAR-MAP-3-COLOR.
(一个平面三着色问题是可以跟一个平面图三着色问题相互规约的!)
1.1 证明

2.1 Planar 3-colorability is NP-complete
证明:1.首先证明它是一个NP问题很好证明只要我们在多项式时间内找到其中一个解就行了。
2.我们可以将3着色问题规约到平面3着色问题。
3.给你任意一个3着色实例G我们都能构造一个平面3着色的实例,如果这个平面是可以被3着色的,那么G就是可2着色的。
2.1.1 平面3着色特点
每一个平面如果可以被3着色那么相反的角具有相同的颜色,依次可以推出其他颜色。
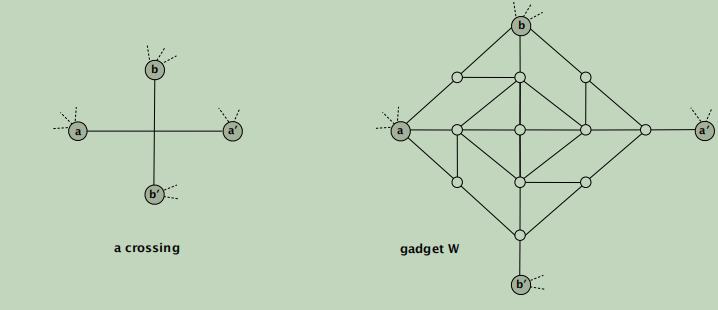
Lemma. W is a planar graph such that:
・In any 3-coloring of W, opposite corners have the same color.
・Any assignment of colors to the corners in which opposite corners have
the same color extends to a 3-coloring of W.
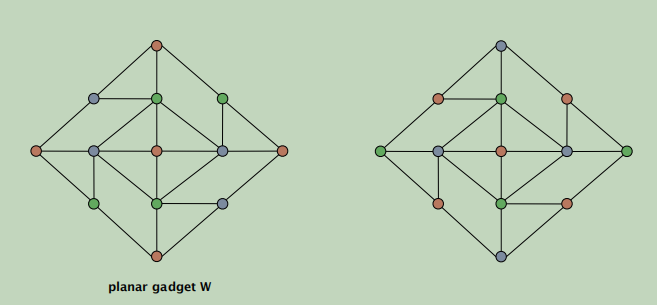
Pf. The only 3-colorings (modulo permutations) of W are shown below. ▪
2.1.2 构造方法
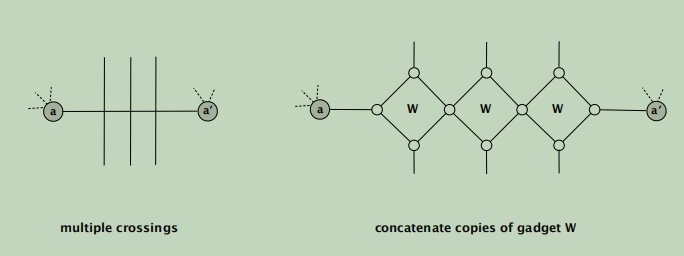
Construction. Given instance G of 3-COLOR, draw G in plane, letting edges
cross. Form planar Gʹ by replacing each edge crossing with planar gadget W.
Lemma. G is 3-colorable iff Gʹ is 3-colorable.
・In any 3-coloring of W, a ≠ aʹ and b ≠ bʹ.
・If a ≠ aʹ and b ≠ bʹ then can extend to a 3-coloring of W.