第五章《优化程序性能》教材重点知识总结和理解
1. 为什么要优化程序性能?
1. 运行过慢的程序无法提供应有的功能。
2. 对于计算量很多大的程序来说一点点优化对程序的功能效率的提高非常大
2. 权衡实现和维护程序的简单性与程序的运行速度
void psum(float a[],float p[],long n)
{
long i;
p[0] = a[0];
for(i=1;i<n;i++)
{
p[i]=p[i-1]+a[i];
}
}
void psum2(float a[],float p[],long n)
{
long i;
p[0] = a[0];
for(i=1;i<n-1;i+=2)
{
float mid_val = p[i-1]+a[i];
p[i] = mid_val;
p[i+1] = mid_val + a[i+1];
}
if(i<n)
p[i] = p[i-1] + a[i];
}
以上两段代码表达的是同样的含义即对于两个向量的定义。
但是当我们第一次看到第二段程序中函数功能的表现效果远逊于第一个,同时第二段程序应能提高一倍循环效率。
3. 程序本身的安全性和系统优化
在gcc编译过程中如果加上
-O1 -O2等参数时会使用系统的优化功能功能,这种优化实在系统确定程序本身是安全的时候进行的。
这提醒我们在进行编译的系统优化时要首先注意编译程序的边界测试,特殊值使用时会出现的问题,指针变量使用给程序带来的风险等问题。
Amdahl定律
S=1/((1-a) + a/k);
S为加速比,
a为可加速部分的百分比
K为对a部分加速的倍数
4. 优化代码性能的三种方式:(指不依赖目标机器性能的优化)
1. 消除循环低效率
char combine1_descr[] = "combine1: Maximum use of data abstraction";
/* $begin combine1 */
/* Implementation with maximum use of data abstraction */
void combine1(vec_ptr v, data_t *dest)
{
int i;
*dest = IDENT;
for (i = 0; i < vec_length(v); i++) {
data_t val;
get_vec_element(v, i, &val);
/* $begin combineline */
*dest = *dest OPER val;
/* $end combineline */
}
}
/* $end combine1 */
char combine2_descr[] = "combine2: Take vec_length() out of loop";
/* $begin combine2 */
/* Move call to vec_length out of loop */
void combine2(vec_ptr v, data_t *dest)
{
int i;
int length = vec_length(v);
*dest = IDENT;
for (i = 0; i < length; i++) {
data_t val;
get_vec_element(v, i, &val);
*dest = *dest OPER val;
}
}
combine2函数通过把vec-length移出循环,大大缩减了代码的时钟周期。
代码移动运用于包含迭代的的代码中,能有效消除循环的低效率。
但是代码移动是不能由优化编译器来完成,而必须依靠程序员自己。
表现出的是编程中常见的问题或者说一些不好的习惯所导致的代码片段导致的隐藏的渐进低效率。
2. 减少过程调用
尽管过程调用能保证程序的模块性,但是在一些包含迭代的大型程序中,过程调用会带来相当大的开销。
因此单单考虑提高程序性能,因尽量减少过程调用。
如书中combine3函数,放弃了函数调用,而直接进行数据访问,无疑能大大提高程序性能。
3. 消除不必要的内存引用
在这里,通俗的可以理解为在编程过程中尽量减少指针变量的重复使用,以减少访问内存的次数。可以从combine4和combine3对比看出这一点。
而且从这一节我们能进一步理解,系统在进行编程的过程中是根据自己对程序的理解进行优化,编译。
从这一点我们也能更清楚地认识编程的过程即是向机器解释自己的意图,所以编程的过程中我们应该尽量去考虑机器编译时会考虑的问题,以全面表达我们编程的意图。
5. 理解现代处理器
- 超标量:在每个时钟周期执行多个操作,而且是乱序的。
- 整个设计包括两个主要部分:
- ICU:负责从存储器中读出指令序列,并根据这些指令序列生成一组针对程序数据的基本操作。
- EU:负责执行以上操作。

- 处理器操作的抽象问题:
以combine4为例通过其汇编代码画数据流图,便于计算和理解

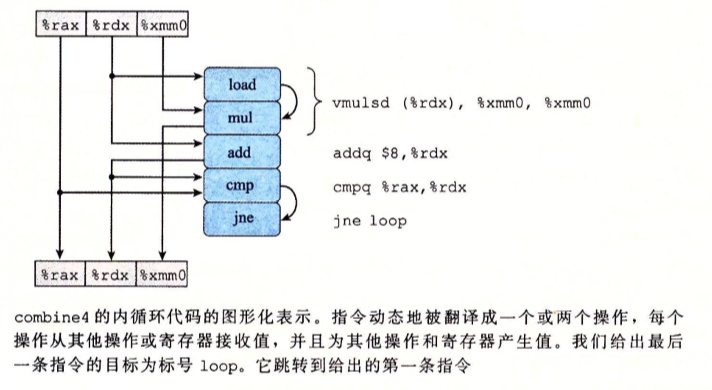
-
ICU从指令告诉缓存中读取指令,指令告诉缓存是一个特殊的告诉缓存储存器,它包括最近访问的指令。
通常,ICU会在当前正在执行的指令很早之前取指,所以它有组后的时间对指令解码,并操作发送到EU,不过会遇到分支问题。
-
分支预测:处理器预测是否分支,并预测分支的目标地址。
-
投机执行:取出预测的分支处的指令并对指令解码。
-
功能单元的性能:
- 周期计数值:执行时间和发射时间。
- 发射时间指明一个单元的连续操作之间的周期数,在一个流水线化的单元中,发射时间比执行时间短。
6. 循环展开
- 循环展开是常见的低级程序优化方法的一种,目的是让进一步优化成为可能
- k*1的循环展开不能将性能改进到超过延迟界限。
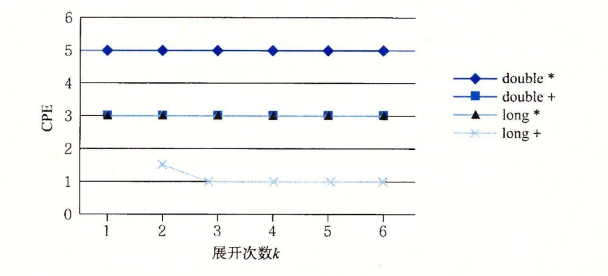
7. 限制性因素
- 寄存器溢出
- 分支预测和预测错误处罚
学习中的疑问和思考
问题一:
在学习C语言编程的时候,老师曾经说,使用指针可以提高程序的效率。
当时我不是很能理解其中的细节和原理。
但现在看来,好像减少指针的使用反而能提告速度,这又是为什么呢?
问题一的思考:
指针的优点:
a.为函数提供修改调用变元的灵活手段;
b.支持C 动态分配子程序
c.可以改善某些子程序的效率
>>在数据传递时,如果数据块较大(比如说数据缓冲区或比较大的结构),
这时就可以使用指针传递地址而不是实际数据,即提高传输速度,又节省大量内存。
d.为动态数据结构(如二叉树、链表)提供支持
问题二:
习题5.5、5.6中根据Willianm.G.Honor所提出的反复提出x的幂以减少乘法运算次数,为何运算次数减少后比之前的速度还要慢?
问题二的思考:
首先,CPU加法器和乘法器是完全流水线化的。
也就是说可以做到指令级并行
(可以把乘法器看成是一条生产线,cpu把一条乘法语句的计算分为若干步骤,像过关一样,第一条乘法语句过了第一关,第二条乘法指令就可以去过第一关了,就像工厂的流水线生产一样),那么一条乘法语句和两条乘法语句是没有区别的。
然后再看计算方式,poly函数中的result只跟a[i]*xpwr的结果有关。
polyh函数中的result跟a[i]+x*result的结果有关,换成汇编,前者可能只需要两条乘法指令(两条可以并行)一条传送指令就够了,但是后者却需要一条乘法指令一条加法指令(且无法并行,因为加法指令依赖于前面的乘法指令)和一条传送指令。
那么想当然执行一条乘法指令的时间要比执行一条乘法指令和一条加法指令的时间短。
总而言之poly函数中计算之间的相关性比较小,而polyh中计算之间的相关性大,就造成了这种结果
问题三:练习题5.5
对多项式求值a0+a1x+a2x^2+...+an*x^n。
代码如下:
double poly(double a[], double x, int degree)
{
long int i;
double result = a[0];
double xpwr = x;
for ( i = 1; i <= degree; i++)
{
result += a[i] * xpwr;
xpwr = x * xpwr;
}
return result;
}
答案为在参考机Core i7上,测量这个函数的CPE等于5.00。
为什么a[i] * xpwr这个代码不算入对result的更新的时钟周期?
如果按照我的想法CPE应该是5+3。
问题三的思考:
这就是流水线处理处理器的特点。
5.5题的程序,因为result和后边的两个数据没有关联,所以加法指令可以在译码阶段直接取得执行阶段的浮点运算的成果。
因此在循环迭代过程中,加法不会影响循环的每元素周期数。
但是对于5.6题就不同了,表达式更新result值与自身关联,必须先提取result原来的值,在没有进行浮点乘法的情况下不能进行浮点加法,浮点加法没有结束也不能更新result因为他在关键路径上。
我觉得理解这个问题的关键是循环是一个周而复始的过程,流水线结构上的指令也是连续不断的,只割裂执行的一个环节很难想通这个问题。
5.5也可以这么思考,两个浮点乘法运算相互关联,一前一后执行,第一条浮点运算的结果被保存(参看5.7.1关于转发的论述),浮点加法每次取更新后的值进行运算。把这个循环拉开,浮点加法就好像站在流水线旁边扫条码的工人,不影响生产进度。
因为流水线生产的速度,比他扫描的速度慢。
同时可以根据其汇编代码画图可能更为准确清楚。
问题四:
如何理解代码的可预测和不可预测
问题四的思考:
关于代码的分支预测所带来的分支预测错误,我认为实际上是对我们写代码或修改代码的一种提示。
在写代码时要注意在设置单一条件时不要将条件语句之后要执行的命令过度细化,尽量使条件语句后的分支执行内容简化。
不可预测的代码即是不可预知分支错误的代码,而可预测的代码是指其分支效率在系统预测执行的情况下也可以被预测。
教材习题总结
练习题只给出部分的思考,具体参见教材课后习题答案。
5.1
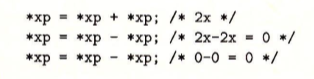
5.2
这道题可以通过画函数图像得到答案,由于n只能是整数,因此情况分别是:n <=2时,版本1最快,3<=n<=7时,版本2最快,当n>=8时 ,版本3最快
5.4 优化版本

5.7

可以从CPE结果看出,没有一个低于其延迟界限
5.13
A.

B.CPE下界是浮点加法的延迟。
C.两个load操作的吞吐量界限。
D. 因为乘法不在关键路径上,乘法也是流水线执行的,其限制因素为吞吐量界限。整个程序的限制因素为最后的浮点数加法的延迟,这个延迟对float和double都是3.00。
5.14
void inner4(vec_ptr u, vec_ptr v, data_t *dest)
{
long int i;
int length = vec_length(u);
data_t *udata = get_vec_start(u);
data_t *vdata = get_vec_start(v);
data_t sum = (data_t) 0;
int limit = length - 2;
for (i = 0; i < limit; i++) {
sum = sum + udata[i] * vdata[i];
sum = sum + udata[i+1] * vdata[i+1];
sum = sum + udata[i+2] * vdata[i+2];
}
for(; i<length; ++i)
sum = sum + udata[i] * vdata[i];
*dest = sum;
}
A. 因为load吞吐量为1.00,每计算一个值需要两次load,所以CPE不可能低于2.00。
B. 关键路径上仍然有N个浮点加法,所以循环展开并没有改变
5.15
void inner4(vec_ptr u, vec_ptr v, data_t *dest)
{
long int i;
int length = vec_length(u);
data_t *udata = get_vec_start(u);
data_t *vdata = get_vec_start(v);
data_t sum = (data_t) 0;
int limit = length - 2;
for (i = 0; i < limit; i++) {
int x1 = udata[i] * vdata[i];
int x2 = udata[i+1] * vdata[i+1];
int x3 = udata[i+2] * vdata[i+2];
sum = sum + (x1 + x2 + x3);
}
for(; i<length; ++i)
sum = sum + udata[i] * vdata[i];
*dest = sum;
}
5.17
void *optimized_memset(void *s, int c, size_t n)
{
unsigned int K = sizeof(unsigned long);
unsigned char *schar = (unsigned char*)s;
unsigned long *lchar;
unsigned long fill = 0;
int i = 0;
for(i = 0; i < K; i++)
fill += (c&0xff) << (i<<3);
// n如果是个负数,会变成一个很大的正数,这应该不需要处理吧?
// size_t应该是unsigned int,n应该不可能是
//一般K都是2的整数次幂,也可以用schar&(K-1)来求schar%K
while((unsigned)schar%K && n)
{
*schar++ = (unsigned char)c;
n--;
}
lchar = (unsigned long*) schar;
while ( n >= K ) {
*lchar++ = fill;
n -= K; //不知道这里如果用++和--会不会影响整体的效率
}
schar = (unsigned char*) lchar;
while(n) //剩余的n
{
*schar++ = (unsigned char)c;
--n;
}
return s;
}
5.18
double poly_optimized(double a[], double x, int degree)
{
long int i;
double result = 0;
double s = 0, powx4 = 1;
double x2 = x*x;
double x4 = x2*x2;
long int limit = degree-3;
for(i = 0; i <= limit; i += 4)
{
double v1 = a[i] + a[i+1]*x;
double v2 = a[i+2] + a[i+3]*x;
v1 = v1 + v2 * x2;
s = s + v1 * powx4;
powx4 *= x4;
}
for(; i <= degree; ++i)
{
s += a[i]*powx4;
powx4 *= x;
}
return s;
}
关键路径就是一个浮点数乘法,因此CPE是浮点乘法延迟的1/4,然而每次计算都需要load 4个值,所以CPE还是1.00。
5.19
void psum(float a[], float p[], long int n)
{
long int i;
int v = 0;
for(i=0; i<n-1; i+=2)
{
int v1 = a[i];
int v2 = a[i+1];
v2 = v1 + v2;
p[i] = v + v1;
p[i+1] = v + v2;
v = v + v2;
}
for(; i<n; i++)
{
v = v + a[i];
p[i] = v;
}
}
代码链接
结对学习情况
结对对象:20155204王昊
本周结对小组同学的学习内容是第11章,我们对这两章的基本内容进行了交流,对彼此的疑问进行了讨论,一起查阅了相关资料。