梯度下降

 

 

---

概念

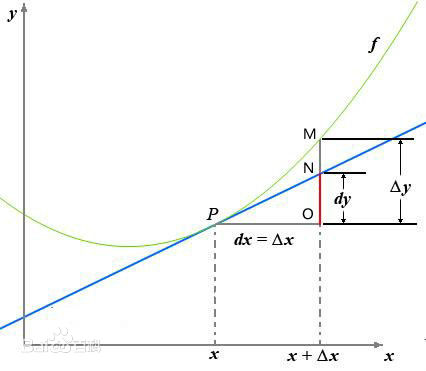
导数：函数y=f(x)在某一点处理沿x轴正方向的变化 率/变化趋势。针对一元函数

 

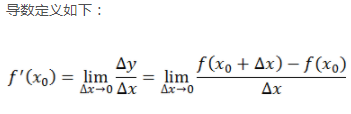
偏导数：函数在坐标轴方向的变化率。针对多元函数　

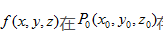　点上各个坐标轴方向的偏导数，记作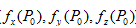

方向导数：函数在其它特定方向上的变化率

  

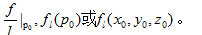
梯度：函数在某个点各坐标轴方向上的偏导数组成的向量

  

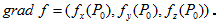
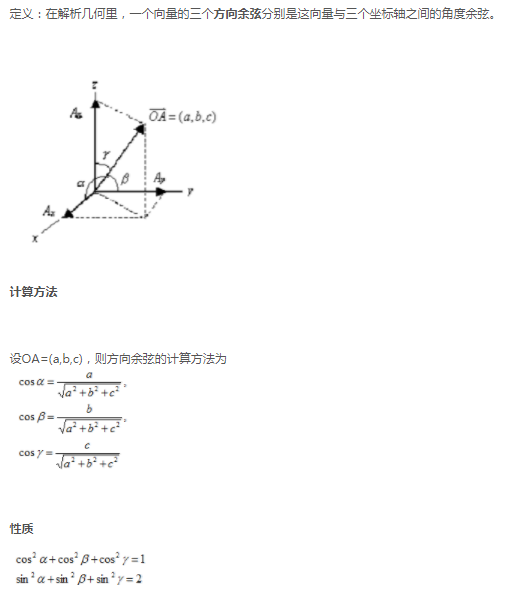
梯度是一个向量，是一个n元函数f关于n个变量的偏导数，比如三元函数f的梯度为(f_x,f_y,f_z)，二元函数f的梯度为(f_x,f_y），一元函数f的梯度为f_x。然后要明白梯度的方向是函数f增长最快的方向，梯度的反方向是f降低最快的方向。

梯度是标量变化最大方向的变化率。

梯度是三维空间里的导数，斜率是二维空间里的导数，也可以说斜率是梯度的二维特例。

梯度的方向就是函数增加最快的方向，梯度的大小就是沿这个方向的斜率。

举例：假如你现在站在山顶上往下看，其中最陡的方向就是梯度的方向，这个方向的斜率就是梯度的大小，函数就是位置。

梯度的提出只为回答一个问题： 
　函数在变量空间的某一点处，沿着哪一个方向有最大的变化率？ 
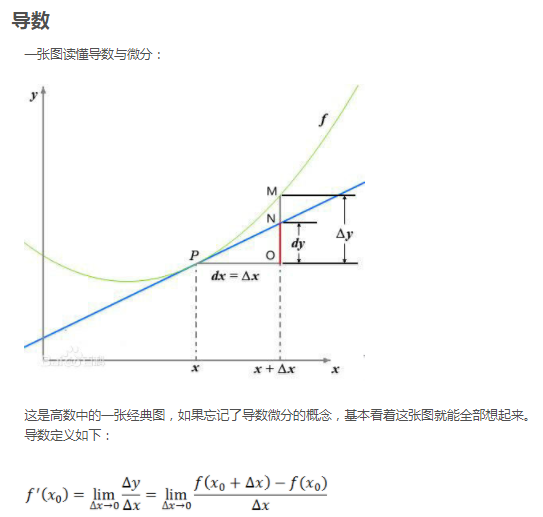
　梯度定义如下： 
　函数在某一点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。而在所有方向中，与(f_x(x_k),f_y(y_k))夹角为0的方向，其方向导数最大，恰好等于(f_x(x_k),f_y(y_k))。（定义2） 　　

　这里注意三点： 
　1）梯度是一个向量，即有方向有大小； 
　2）梯度的方向是最大方向导数的方向； 
　3）梯度的值是最大方向导数的值。 

 　　

---

梯度下降

梯度下降算法：

1）随机初始值；

2）迭代，直至收敛。表示在处的负梯度方向，表示学习率。

即：沿着负梯度方向例f最快下降

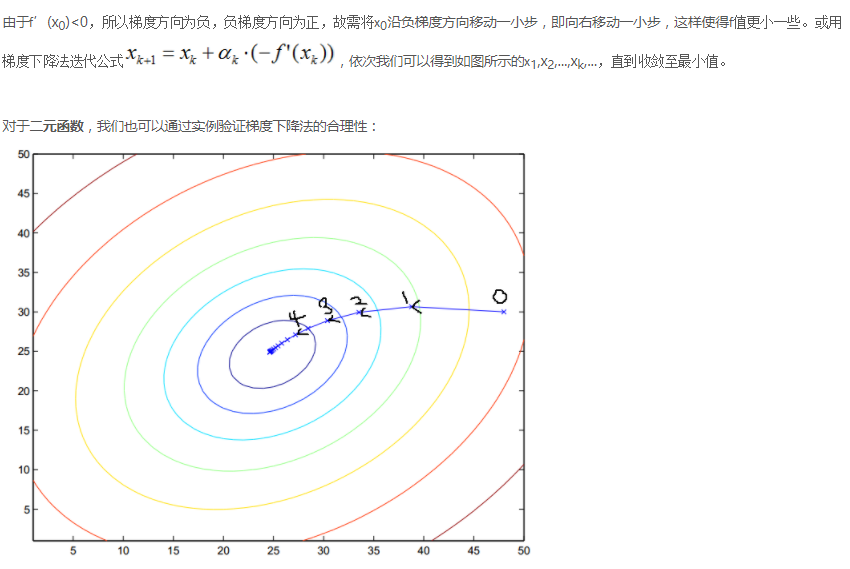
以二元函数为例，在每次得到一个点(x_k,y_k)时，需要计算f在该点的梯度向量(f_x(x_k),f_y(y_k))，这个方向表示f增长最快的方向，-(f_x(x_k),f_y(y_k))表示f下降最快的方向，故只需将(x_k,y_k)沿着-(f_x(x_k),f_y(y_k))这个方向移动一小步，就可以减少f的值，直至收敛到最小值。

关于梯度下降：

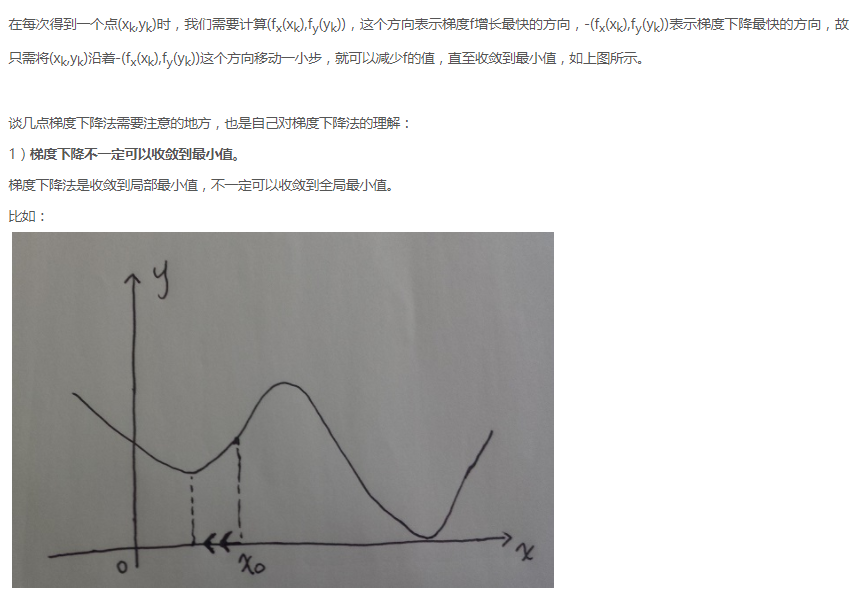
1、 梯度下降不一定可以收敛到最小值

梯度下降法是收敛到局部最小值，不一定可以收敛到全局最小值。

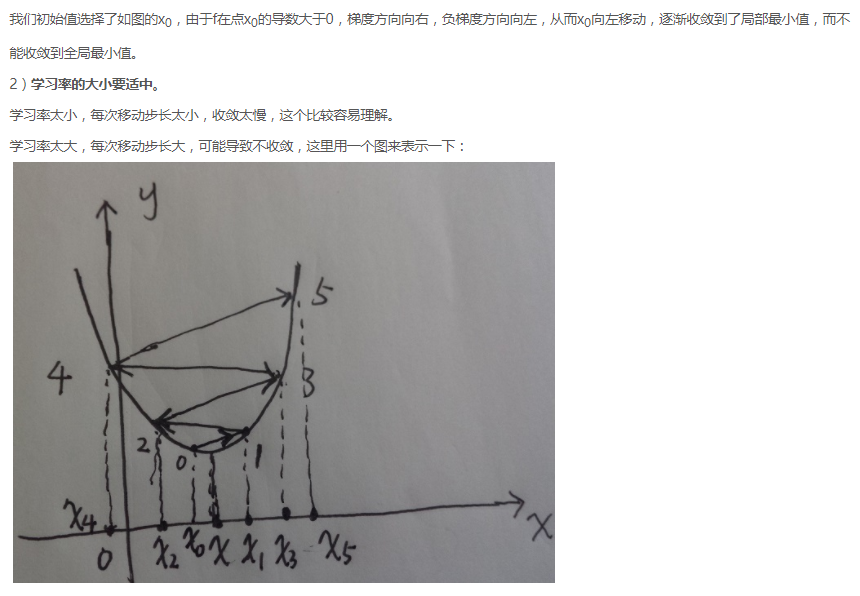
2、学习率的大小要适中

学习率太小，每次移动步长太小，收敛太慢。

学习率太大，每次移动步长大，可能导致不收敛。

3、负梯度方向是所有方向（该点的各个方向导数）中使f值下降最快的方向，可以使f更快的收敛。 

---

概念参考：http://blog.csdn.net/zhulf0804/article/details/52238435

 

 

---

梯度下降参考：http://blog.csdn.net/zhulf0804/article/details/52250220

---

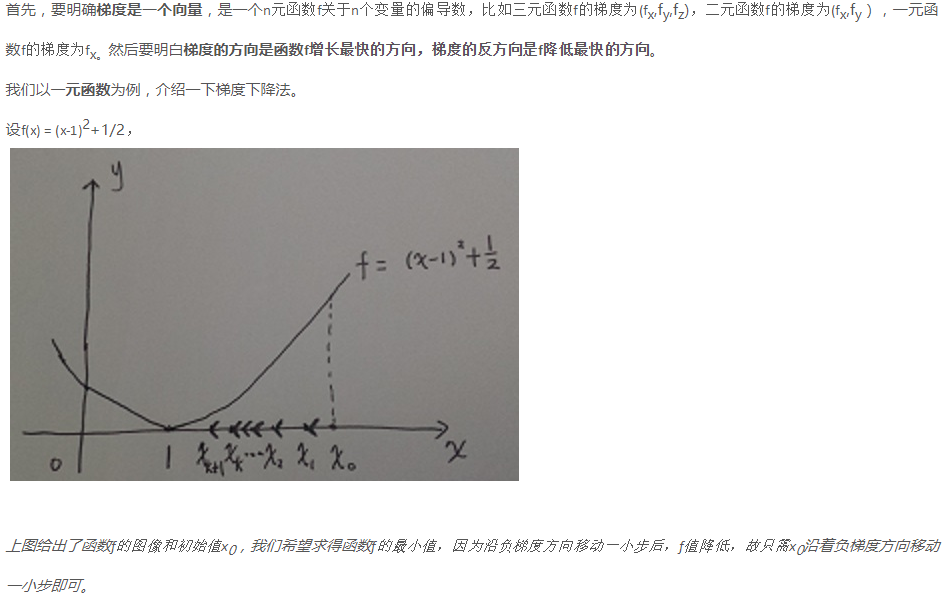
 参考：http://blog.csdn.net/walilk/article/details/50978864

---

参考：

http://blog.csdn.net/zhulf0804/article/details/52238435

http://blog.csdn.net/zhulf0804/article/details/52250220

http://blog.csdn.net/walilk/article/details/50978864

http://news.mydrivers.com/1/530/530260.htm

https://segmentfault.com/a/1190000011994447

https://www.zhihu.com/question/20822481

https://www.zhihu.com/question/26006703/answer/126777449