算法基础

1. 算法概念

数据结构：变量的存储（列表、栈、队列等……）

算法：一个计算过程，解决问题的方法，是计算机的灵魂。

一个算法应该具有以下七个重要的特征：

• ①有穷性（Finiteness）：算法的有穷性是指算法必须能在执行有限个步骤之后终止；

• ②确切性(Definiteness)：算法的每一步骤必须有确切的定义；

• ③输入项(Input)：一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输 入是指算法本身定出了初始条件；

• ④输出项(Output)：一个算法有一个或多个输出，以反映对输入数据加工后的结果。没 有输出的算法是毫无意义的；

• ⑤可行性(Effectiveness)：算法中执行的任何计算步骤都是可以被分解为基本的可执行 的操作步，即每个计算步都可以在有限时间内完成（也称之为有效性）；

• ⑥高效性(High efficiency)：执行速度快，占用资源少；

• ⑦健壮性(Robustness)：对数据响应正确。

2. 时间复杂度

•  时间复杂度是用来评估算法运行效率的一个式子(单位)

　　

• 常见的时间复杂度（按效率排序）

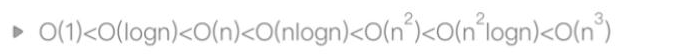
• 复杂问题的时间复杂度

• 一般来说，时间复杂度高的算法比复杂度低的算法运行速度慢，如下图

　　　　由图中我们可以看出，当 n 趋于无穷大时，O(nlogn) 的性能显然要比 O(n!) 来的高

• 代码举例

# O(1)
print('hello')

# O(n)
def complexn(n):
    for i in range(n):
        print(i)

# O(n**2)
def complexn2(n):
    for i in range(n):
        print(i)
        for j in range(n-1):
            print(j)

 # O(log n)
   #当算法过程中出现循环折半的时候，复杂度式子会出现log n
   def complexlo2(n):
      while(n >1):
          print(n)
          n = n//2
   # while的分析思路：
#     假如n = 64的时候会输出：
64
32
16
8
4
2

# 这时候可以发现程序执行了6次

•  如何快速判断时间复杂度

1. 一般来说，只要算法中不存在循环语句，其时间复杂度就是 O(1)

2. 循环减半的过程-》O(log n)

3. 几次循环就是n的几次方的复杂度

空间复杂度

递归

1. 递归最大的两个特点：

• 调用自身

• 结束条件

2 .判断一下下面那些函数是递归函数？

def fun1(x):
    # 这个函数不是递归函数，因为它没有结束条件
    print(x)
    fun1(x-1)

def fun2(x):
    # 这个函数不是递归函数，因为它有了条件之后，会是死循环
    if(x < 0):
        print(x)
        fun2(x+1)

# 先打印后递归
def fun3(x):
    if(x > 0):
        print(x)
        fun3(x-1)
fun3(3) # 会打印 3 2 1

# 先递归后打印
def fun4(x):
    if(x > 0):
        fun4(x-1)
        print(x)
fun4(3) # 会打印 1 2 3

3 .递归练习题

汉诺塔问题

 

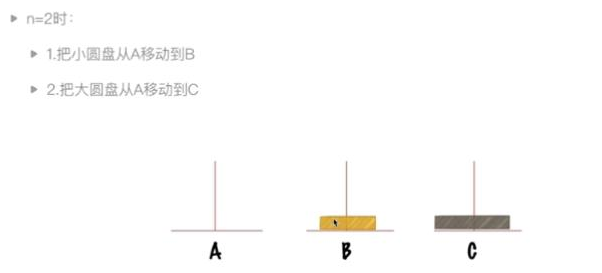
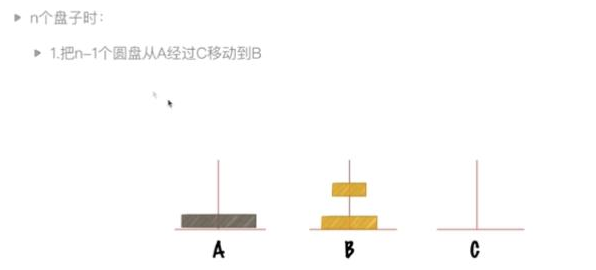
代码实现

'''递归练习：汉诺塔问题

解决思路：

假设有n个盘子：

1.把n-1个圆盘从A经过C移动到B
2.把第n个圆盘从A移动到C
3.把n-1个小圆盘从B经过A移动到C
'''
cnt = 0 #移动次数
def hannoi(n, a, b, c):
    global cnt
    if(n == 1):
        print(a,'MOVE',c)
        cnt += 1
    else:
        #将n-1个盘子从a经过c移动到b
        hannoi(n-1, a, c, b)
        #将最后一个大盘子从a移动到c
        print(a, 'MOVE', c)
        cnt += 1
        #将n-1个盘子从b经过a移动到c
        hannoi(n-1, b, a, c)

hannoi(3,'A柱','B柱','C柱')
print('移动次数=',cnt)

>>输出结果
A柱 MOVE C柱
A柱 MOVE B柱
C柱 MOVE B柱
A柱 MOVE C柱
B柱 MOVE A柱
B柱 MOVE C柱
A柱 MOVE C柱
移动次数= 7

汉诺塔移动次数递推公式为f(x)=2f(x-1)+1

经过推导移动次数为f(x)=2**x -1(n为盘子数）

推导通项公式。由f（k）=2f（k-1）+1得f(k)+1=2(f(k-1)+1)，于是{f(k)+1}是首项为f(1)=1，公比为2的等比数列，求得f(k)+1 = 2^k，所以f(k) = 2^k-1

 

 参考http://www.cnblogs.com/haiyan123/p/8394931.html