2018冬令营模拟测试赛(十一)
[Problem A]小Y增员操直播群
试题描述


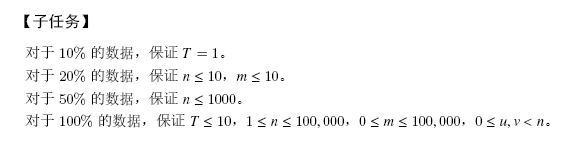
输入
见“试题描述”
输出
见“试题描述”
输入示例
见“试题描述”
输出示例
见“试题描述”
数据规模及约定
见“试题描述”
题解
这题其实就是个暴力……
从后往前扫一遍,对于编号为 (i) 的人,找到和他互膜的编号最小的人 (j),那么 (j) 和 (i) 一定属于不同组。但注意这时 (j) 不一定是左边组的最后一个成员,所以需要往前推,一直到某个 (i') 对应的 (j' = 0) 之后,再下一个对应的互膜的人才是左边组的最后一个成员……
情况挺多的总之想到从后往前扫就不难做了。(为什么从后往前?因为右边组的人数大于等于左边的人数,所以右边每个人有且仅有一次和左边的人互膜)
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <vector>
using namespace std;
#define rep(i, s, t) for(int i = (s); i <= (t); i++)
#define dwn(i, s, t) for(int i = (s); i >= (t); i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 100010
int n, m, hd[maxn];
vector <int> lft[maxn];
int solve(int l, int r, int dep) {
// printf("solve [%d, %d] %d
", l, r, dep);
if(l == r) return hd[r] >= lft[r].size() ? dep : -1;
int mx = -1, i;
for(i = r; i > mx; i--) {
if(hd[i] >= lft[i].size()) return -1;
int mylft = lft[i][hd[i]++];
if(mx < 0) mx = mylft;
if(mx - mylft != r - i) return -1;
if(!(mylft - l) && i > mx + 1) {
i--;
if(hd[i] >= lft[i].size()) return -1;
mx = lft[i][hd[i]];
break;
}
}
for(; i > mx; i--) if(hd[i] >= lft[i].size() || lft[i][hd[i]++] - l != (i - l) % (mx - l + 1)) return -1;
if(mx - l + 1 > r - mx) return -1;
int lans = solve(l, mx, dep + 1), rans;
if(lans < 0) return lans;
rans = solve(mx + 1, r, dep + 1);
if(rans < 0) return rans;
return max(lans, rans);
}
void work() {
rep(i, 0, n - 1) lft[i].clear();
bool ok = 1;
n = read(); m = read();
rep(i, 1, m) {
int a = read(), b = read();
if(a == b) ok = 0;
if(a > b) swap(a, b);
lft[b].push_back(a);
}
if(!ok) return (void)puts("-1");
rep(i, 0, n - 1) sort(lft[i].begin(), lft[i].end()), hd[i] = 0;
int ans = solve(0, n - 1, 0);
printf("%d
", ans);
return ;
}
int main() {
int T = read();
while(T--) work();
return 0;
}
[Problem B]小J真爱粉交流群
试题描述


输入
见“试题描述”
输出
见“试题描述”
输入示例
见“试题描述”
输出示例
见“试题描述”
数据规模及约定
见“试题描述”
题解
仔细想来,有这么几个性质:
-
每次大敦操作后,小 J 至多放一堵墙(首先一堵一堵放肯定来得及;如果一下放很多反而可能起不到“诱导”作用,如果第一步把墙放完,那么大墩的路径已经固定下来了,大墩就可以针对这个路径走一条最短路;如果一步一步放,大墩还按照贪心的最短路来,就可以把他逼到一个角然后再返回,从而增大他的得分);
-
每次小 J 如果放墙,一定放在大墩的棋子下面(这个显然);
-
如果小 J 不放墙,大墩一定往下走一格(好不容易给一个不会被逼到角的机会一定得抓住,因为往下走一行无论初始位置在哪小 J 都有办法把大墩逼到小 J 想让他去的位置);
-
任何时刻大墩棋子下方的一排墙一定是一段连续的区间(根据上两条可得)。
(至于那个大墩不可能往上走啥的就不必再提了……)
于是针对这几条性质可以设计一个 dp。(f(i, l, r)) 表示棋子处于第 (i) 行,该行下方的墙铺在了区间 ([l, r]),棋子在左边(即坐标 ((i, l - 1)));(g(i, l, r)) 表示棋子处于第 (i) 行,该行下方墙铺在了区间 ([l, r]),棋子在右边(即坐标 ((i, r + 1)))。
因为是大墩先选一个位置放棋子,所以转移的时候是考虑小 J 决策是否在他棋子下面放墙。
-
若放墙,则轮到大墩决策走到墙的最左端还是最右端,这两种决策取较小值;
-
若不放墙,则大墩往下走一格;
放、不放墙两种决策取最大值。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <vector>
using namespace std;
#define rep(i, s, t) for(int i = (s); i <= (t); i++)
#define dwn(i, s, t) for(int i = (s); i >= (t); i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 110
#define oo 2147483647
int n, m, A[maxn][maxn], S[maxn][maxn], f[maxn][maxn][maxn], g[maxn][maxn][maxn]; // f for left, g for right
void upmx(int& a, int b) {
if(a < b) a = b;
return ;
}
void upmn(int& a, int b) {
if(a > b) a = b;
return ;
}
void dp(int i, int l, int r) {
if((l - 1 >= m || l - 1 < 1 || f[i][l][r] >= 0) && (r + 1 <= 1 || r + 1 > m || g[i][l][r] >= 0)) return ;
if(i == n) return (void)(f[i][l][r] = g[i][l][r] = 0);
int t1, t2;
if(1 <= l - 1 && l - 1 < m) {
t1 = oo; t2 = -1;
if(l > 1 && !(l - 1 == 1 && max(r, l - 1) == m)) {
dp(i, l - 1, max(r, l - 1));
if(1 <= l - 2) upmn(t1, f[i][l-1][max(r,l-1)] + A[i][l-2]); // , printf("%d %d %d toleft %d %d %d
", i, l, r, i, l - 1, max(r, l - 1));
if(max(r, l - 1) + 1 <= m) upmn(t1, g[i][l-1][max(r,l-1)] + S[i][max(r,l-1)+1] - S[i][l-1]); // , printf("%d %d %d toright %d %d %d
", i, l, r, i, l - 1, max(r, l - 1));
}
if(t1 == oo) t1 = -1;
dp(i + 1, l, 0);
t2 = f[i+1][l][0] + A[i+1][l-1];
f[i][l][r] = max(t1, t2);
}
if(m >= r + 1 && r + 1 > 1) {
t1 = oo; t2 = -1;
if(r < m && !(min(l, r + 1) == 1 && r + 1 == m)) {
dp(i, min(l, r + 1), r + 1);
if(r + 2 <= m) upmn(t1, g[i][min(l,r+1)][r+1] + A[i][r+2]); // , printf("%d %d %d toright %d %d %d
", i, l, r, i, min(l, r + 1), r + 1);
if(1 <= min(l, r + 1) - 1) upmn(t1, f[i][min(l,r+1)][r+1] + S[i][r] - S[i][min(l,r+1)-2]); // , printf("%d %d %d toleft %d %d %d
", i, l, r, i, min(l, r + 1), r + 1);
}
if(t1 == oo) t1 = -1;
dp(i + 1, m + 1, r);
t2 = g[i+1][m+1][r] + A[i+1][r+1];
g[i][l][r] = max(t1, t2);
}
/*printf("hasf: %d, hasg: %d
", 1 <= l - 1 && l - 1 < m, m >= r + 1 && r + 1 > 1);
printf("[%d][%d][%d] %d %d
", i, l, r, f[i][l][r], g[i][l][r]); // */
return ;
}
void work() {
n = read(); m = read();
rep(i, 1, n) rep(j, 1, m) A[i][j] = read(), S[i][j] = S[i][j-1] + A[i][j];
if(m == 1) {
int sum = 0;
rep(i, 1, n) sum += A[i][1];
printf("%d
", sum);
return ;
}
memset(f, -1, sizeof(f)); memset(g, -1, sizeof(g));
int ans = oo;
rep(i, 1, m) {
if(i < m) dp(1, i + 1, 0), upmn(ans, f[1][i+1][0] + A[1][i]);
if(i > 1) dp(1, m + 1, i - 1), upmn(ans, g[1][m+1][i-1] + A[1][i]);
}
printf("%d
", ans);
return ;
}
int main() {
int T = read();
while(T--) work();
return 0;
}
[Problem C]青青草原播种计划
试题描述




输入
见“试题描述”
输出
见“试题描述”
输入示例
见“试题描述”
输出示例
见“试题描述”
数据规模及约定
见“试题描述”
题解
这就是一道大数据结构题咯(其实也不算太大)。
这个可持久化是假的,只有询问,不要被吓到……直接对于每个助手开一个 vector,时间倒流的时候二分一下就好了。
询问是经典的求 (mex)(最小没出现的数字)和最小不可表数。
第一问直接线段树维护最长前缀即可,第二问我用的 (O(mathrm{log}^2n)) 的做法,先假设 (ans = 0),然后若 (sum[1, ans + 1] > ans) 就更新 (ans = sum[1, ans + 1])((sum[l, r]) 表示权值在 ([l, r]) 中的数的和),否则跳出(由于每次至少增加一倍,所以至多调用 (mathrm{log}n) 次 (sum[l, r]))。只需要维护区间最长连续前缀和区间和即可。
事实上第二问可以也用线段树维护做到一个 (mathrm{log}):考虑每个节点如果左儿子都能表出,且左儿子区间和大于等于右儿子区间最小值,则该节点的权值都能够被表出。
合并的时候可以直接用线段树合并。(这好像是我第一次成功写出线段树合并,居然还是考场上写出来的……)
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <vector>
using namespace std;
#define rep(i, s, t) for(int i = (s); i <= (t); i++)
#define dwn(i, s, t) for(int i = (s); i >= (t); i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
return x * f;
}
#define maxn 500010
#define maxnode 10000010
#define maxv 500000
#define LL long long
int n, rt[maxn];
struct Info {
int time, ans1; LL ans2;
Info() {}
Info(int _1, int _2, LL _3): time(_1), ans1(_2), ans2(_3) {}
bool operator < (const Info& t) const { return time < t.time; }
};
vector <Info> tline[maxn];
int ToT, lc[maxnode], rc[maxnode], pre[maxnode];
LL sumv[maxnode];
void update(int &o, int l, int r, int p, int v) {
if(!o) o = ++ToT;
if(l == r) {
if(!sumv[o] && v < 0) return ;
sumv[o] += v * p;
if(sumv[o]) pre[o] = 1; else pre[o] = 0;
return ;
}
int mid = l + r >> 1;
if(p <= mid) update(lc[o], l, mid, p, v);
else update(rc[o], mid + 1, r, p, v);
sumv[o] = sumv[lc[o]] + sumv[rc[o]];
pre[o] = (lc[o] && pre[lc[o]] == mid - l + 1) ? (rc[o] ? pre[rc[o]] : 0) + mid - l + 1 : (lc[o] ? pre[lc[o]] : 0);
return ;
}
LL qsum(int o, int l, int r, int ql, int qr) {
if(!o) return 0;
if(ql <= l && r <= qr) return sumv[o];
int mid = l + r >> 1;
LL ans = 0;
if(ql <= mid) ans += qsum(lc[o], l, mid, ql, qr);
if(qr > mid) ans += qsum(rc[o], mid + 1, r, ql, qr);
return ans;
}
LL query(int o) {
LL ans = pre[o];
while(1) {
LL org = ans;
ans = qsum(o, 1, maxv, 1, min(ans + 1, (LL)maxv));
if(ans == org) break;
if(ans >= maxv){ ans = qsum(o, 1, maxv, 1, maxv); break; }
}
return ans + 1;
}
void merge(int& y, int x, int l, int r) {
if(!y){ y = x; return ; }
if(!x) return ;
if(l == r) {
sumv[y] += sumv[x];
if(sumv[y]) pre[y] = 1; else pre[y] = 0;
return ;
}
int mid = l + r >> 1;
merge(lc[y], lc[x], l, mid); merge(rc[y], rc[x], mid + 1, r);
sumv[y] = sumv[lc[y]] + sumv[rc[y]];
pre[y] = (lc[y] && pre[lc[y]] == mid - l + 1) ? (rc[y] ? pre[rc[y]] : 0) + mid - l + 1 : (lc[y] ? pre[lc[y]] : 0);
return ;
}
void getEverything(int o, int l, int r) {
if(!o) return ;
if(l == r) rep(i, 1, sumv[o] / r) printf("%d ", l);
else {
int mid = l + r >> 1;
getEverything(lc[o], l, mid); getEverything(rc[o], mid + 1, r);
}
return ;
}
int lst;
int Get() {
return (read() + lst - 1) % n + 1;
}
int main() {
n = read(); int q = read();
rep(i, 1, n) tline[i].push_back(Info(0, 1, 1));
rep(kase, 1, q) {
int tp = read(), u = Get(), v, g;
if(tp == 1) {
g = read();
// printf("processing: [%d] %d %d %d
", kase, tp, u, g);
update(rt[u], 1, maxv, g, 1);
// printf("rt[%d] = %d
", u, rt[u]);
tline[u].push_back(Info(kase, pre[rt[u]] + 1, query(rt[u])));
}
if(tp == 2) {
g = read();
// printf("processing: [%d] %d %d %d
", kase, tp, u, g);
update(rt[u], 1, maxv, g, -1);
tline[u].push_back(Info(kase, pre[rt[u]] + 1, query(rt[u])));
}
if(tp == 3) {
v = Get();
// printf("processing: [%d] %d %d %d
", kase, tp, u, v);
swap(u, v);
if(u == v) continue;
// u -> v
merge(rt[v], rt[u], 1, maxv);
rt[u] = 0;
tline[v].push_back(Info(kase, pre[rt[v]] + 1, query(rt[v])));
tline[u].push_back(Info(kase, pre[rt[u]] + 1, query(rt[u])));
}
if(tp == 4) {
// printf("processing: [%d] %d %d
", kase, tp, u);
vector <Info> :: iterator it = tline[u].end(); it--;
printf("%d %lld
", lst = it->ans1, it->ans2);
}
if(tp == 5) {
g = read();
// printf("processing: [%d] %d %d %d
", kase, tp, u, g);
vector <Info> :: iterator it = lower_bound(tline[u].begin(), tline[u].end(), Info(g, 0, 0)); it--;
printf("%d %lld
", lst = it->ans1, it->ans2);
}
}
rep(i, 1, n) {
getEverything(rt[i], 1, maxv);
puts("0");
}
return 0;
}