0、参考材料
林轩田 《机器学习基石》
AI有道 《机器学习基石笔记》
1、机器学习
目的是通过演算法 (A) 找到最好的假设 (h) ,使 (h) 接近真实的 (f) 。
其核心问题只有两个:
-
$ E_{in} (h) approx E_{out}(h) $ --- 训练误差接近测试误差
-
$ E_{in} (h) approx 0 $ --- 训练误差尽可能小
这基本上是每个学习机器学习、深度学习的人都明白的问题,机器学习可行性解释了为什么会是这样。
3、机器学习的可行性
考虑一个简单的二分类的例子,我们的输入 (x) 是二进制的、三维的,输出它的类别 (y) ,即 (left {0,1 ight }) 。

我们有8个hypothesis,这8个hypothesis在5个训练样本上分类都是正确的,但是在未知的3个数据上分类各不相同,并且这8个分类的结果只会有1个是正确的。虽然我们在已知数据上获得了很好的结果,(g approx f) ,但是在未知的数据上结果可能完全相反,我们希望的是正确预测从未见过的数据。
(color{red}{数据量太少,模型复杂度太高,出现过拟合})
3.1 对于某个h,如何知道它在未知数据上的表现?
如果我们在hypothesis sets里选择了一个假设 (h) ,如何通过模型在已知数据上的表现推测该假设在未知数据上的效果呢?大数定律,通过霍夫丁不等式(Hoeffding's inequality)。该公式表明,对于一个假设 (h) ,对于in-sample数据和out-sample数据,二者的误差大于某阈值 (varepsilon) 的概率小于一定值。
(color{red}{训练误差和测试误差很接近})
但是这个公式只保证了 $ E_{in} (h) approx E_{out}(h) $ ,但是并不能保证选择的这个假设 (h) 的 $ E_{in} (h) $ 足够小,我们需要可以通过演算法选择好的 (h) 。
3.2 演算法在所有数据集上的计算都有意义吗?
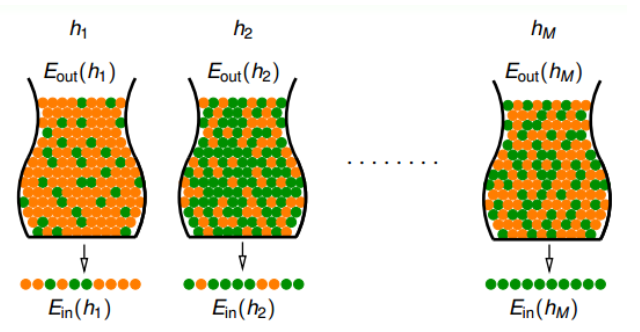
现在我们有 (M) 个假设,每个假设都有对应的数据,对应的 $ E_{in} (h) $ 和 $ E_{out} (h) $ ,前面保证了$ E_{in} (h) $ 和 $ E_{out} (h) $ 十分接近,那么现在直接选一个 $ E_{in} (h) $ 接近零或者等于零的假设就可以吗?不可以。抛硬币的例子告诉我们在假设很多的情况下,出现全是正面的概率非常大。
(color{red}{这里的M个假设不一定相关,即可能一个是y=x^{2}+3,一个是y=4x+0.2568,数据也不是同一批})
所以对于大量的数据集,霍夫丁不等式保证的大多数情况都是好的,但是也不排除出现Bad Data,这是小概率事件,出现Bad Data时,$ E_{in} (h) $ 和 $ E_{out} (h) $ 差别会很大。演算法只有在好的数据集上寻找假设 (h) ,使得$ E_{in} (h) $ 很小才有意义。
3.3 某个数据集是不是Bad Data?
一个数据集,在一个假设 (h) 上是Bad,那么这个数据集就是Bad。Bad Data 的上界为
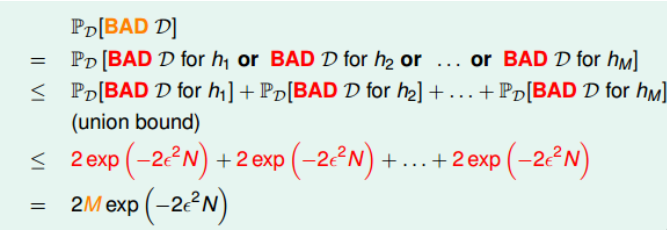
其中 (M) 是假设的个数, (N) 的样本的数量。该union bound表明,当 (M) 有限,且 (N) 足够大时,Bad Data出现的概率很低。
(color{red}{通过推导得出了一个数据集是不是Bad Data,和数据量大小还有应用在这个数据上的假设集有关})
(color{red}{即如果数据量小,假设空间大肯定会出现过拟合,增大数据就可以有效避免过拟合})
当 (M) 有限,且 (N) 足够大时,某个研究问题的某个采样数据集大概率是有效的,即演算法找到的好的假设 (h) 的 $ E_{in} (h) $ 和 $ E_{out} (h) $ 差别不会很大。
但是当M无限大时还可不可以呢?
4、如何缩小M
当 (M) 趋于无穷时,不等式右边的部分会变大,看起来 (P[left | E_{in}(h)-E_{out}(h) ight | >varepsilon]) 的概率会很大,机器学习变得不可行了,但是这是在各假设相对独立的情况下算出的,实际情况不是这样。比如我们会在 (y=ax+b) 的假设空间内通过演算法找一个好的参数,而不是在 (y=x^{2}+3,y=4x+0.2568,...) 这样一堆毫无关联的假设空间内选择。对于有交集的假设集, (M) 实际上没那么大。
我们需要尽可能的缩小 (M) 。
4.1 Effective Number
通过对平面上点的分析,我们知道平面上线的种类是有限的,1个点最多有2种线,2个点最多有4种线,3个点最多有8种线,4个点最多有14( (<2^{4}))种线等等。有效直线的数量总是 (le2^{N}) ,我们可以用 (effective(N)) 代替M。
这样针对平面的情况,我们将无穷大小的 (M) 缩小到了 (effective(N) le 2^{N}) 。
新引入两个概念:
-
dichotomy:将空间中的点用直线或平面分成两类,刚刚提到的平面就是二维空间。
-
growth function:对于由 (N) 个点组成的不同集合中,某集合对应的dichotomy最大,那么这个
dichotomy值就是 (m_{H}(H)) ,上界为 (le2^{N})。[P[left | E_{in}(h)-E_{out}(h) ight | >varepsilon]le 2 cdot m_{H}(H) cdot exp(-2epsilon ^{2}N ) ]
通过对简单空间的分析,得到了四个不同的成长函数:

其中,positive rays和positive intervals的成长函数都是polynomial的,如果用 (m_{H}) 代替 (M) 的话,这两种情况是比较好的。而convex sets的成长函数是exponential的,并不能保证机器学习的可行性。那么,对于2D perceptrons,它的成长函数究竟是polynomial的还是exponential的呢?
再引入一个新的概念:
- break point:视频里称作露出一线曙光的点,就是成长函数不再满足 (2^{N}) 的最小的点。
下面就是这四个成长函数的break point。
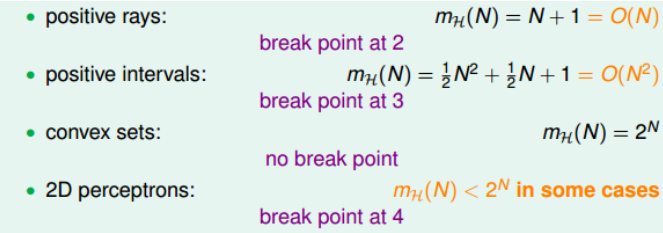
通过观察,我们猜测成长函数可能与break point存在某种关系:对于convex sets,没有break point,它的成长函数是 (2^{N}) ;对于positive rays,break point k=2,它的成长函数是 (O(N)) ;对于positive intervals,break point k=3,它的成长函数是(O(N^{2})) 。则根据这种推论,我们猜测2D perceptrons,它的成长函数 (m_{H}(H)=O(N^{k-1})) 。
4.2 成长函数的上界
引入一个新的函数:
- bounding function:(B(N,k)) 当break point为 (k) ,样本数量为 (N) 时,成长函数的最大值。
通过引入边界函数,将问题进一步抽象,我们不用再关心是1D postive intrervals问题还是2D perceptrons问题。
求解边界函数的过程十分巧妙但是并不困难,需要理解shatter是什么。
通过递推,我们得到了边界函数满足的不等式:
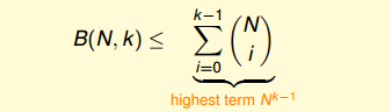
所以成长函数 (m_{H}(H)) 的上界 (B(N,k)) 满足多项式,我们用成长函数替换M没有问题。
4.3 缩放M的整体思路
- (M) 可能是无限大的,比如2D perceptrons,这样 (P[left | E_{in}(h)-E_{out}(h) ight | >varepsilon]le 2 cdot M cdot exp(-2epsilon ^{2}N )) 就没了意义。
- 好在我们的假设集不是毫无关联的,我们可以将假设集分成不同的类别,类别数量为dichotomy,其上界为成长函数 (m_{H}(H)) 。我们将无限的(M) 缩小到了 (2^{N}) ,但是指数级的增长我们仍旧承受不了。
- 好在大多数成长函数都存在break point,使得当 (N>k) 时的增长不再是指数级,但他是不是多项式级增长呢?
- 通过引入成长函数的边界函数(B(N,k)) ,一通推导,证明成长函数的上界是多项式级,那么成长函数在 (N>k) 时的增长自然也是多项式级,所以我们用 (m_{H}(H)) 代替(M) 是没问题的。