判断两个线段是否相交02

写在前面
在其他博客中看到这方面的知识，很多都是重复，并且说的总是云里雾里的，所以这里我就自己总结一下这种问题如何求解，判断两个线段是否相交在前面我们提到了会用到叉积的一点知识，那么这里就来详细说一下怎么判断两个线段是否相交

算法详解
首先我们看一下快速排斥实验，快速排斥实验也就是以两条线段作为对角线做矩形，判断两个矩形是否相交，那么我们这里可以知道：

1）如果两个矩形不相交，那么线段一定不相交

2）如果两个矩形相交，那么线段不一定相交，如下图

 

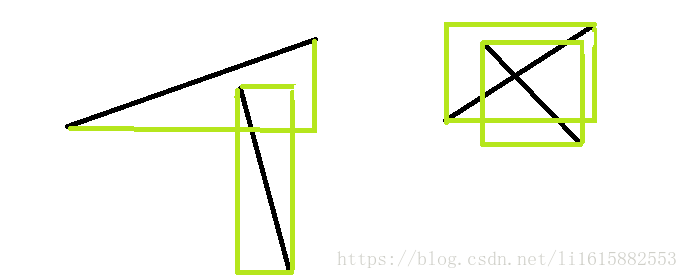
所以这里我们首先就要判断两条线段形成的矩形是否相交，只有相交我们才要继续进行判断后面的线段是否相交.......

跨立实验：前面我们知道叉积可以用来判断两个向量之间的位置关系（顺时针还是逆时针关系），那么这里我们就会用到这个性质

我们知道如果两个线段相交的话，那么一条线段两边的两个点要位于另一条线段的两边，只有两条线段都满足这个条件，我们就可以判定这两条直线相交了，那么我们这里所说的一条线段两个端点位于另一条线段的两边，这就是其他博客中提到的跨立吧

那么我们就用叉积来对是否满足这个条件进行判断：

 

 

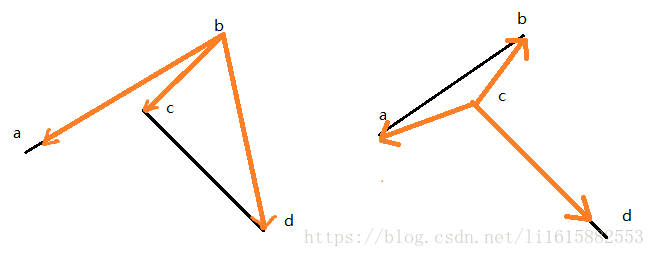
取其中一个向量作为中间向量，中间向量中开始端点作为另外两个向量的起点，判断三个向量之间的位置关系即可：

第一个图中： (ca × cd)(cd × cb) >= 0 我们即可判断满足跨立条件

第二个图中： (bc × ba)(ba × bd) >=0 我们即可判断满足跨立条件

第三个图中： (bc × ba)(ba × bd)  < 0不满足跨立条件

第四个图中： (ca × cd)(cd × cb) >= 0我们即可判断满足跨立条件

即计算(ca × cd)(cd × cb) 与(bc × ba)(ba × bd)的结果必须同时大于零，这两个线段才是相交的；

当然，单独判断其中一个，可以获得一个线段所在的直线是否与另一个线段相交。

那么我们就可以知道上面条件就是判断跨立是否成立的条件了，那么这样我们线段是否相交就已经可以解决了.
栗子及模板
zoj1648

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define INF 0x3f3f3f3f

using namespace std;
const int MAXN = 2100;
struct Point
{
double x,y;
}line[MAXN][2];

double mult(Point p0,Point p1,Point p2) //叉积计算,p0为公用节点
{
return (p0.x - p1.x) * (p0.y - p2.y) - (p0.y - p1.y) * (p0.x - p2.x);
}
//aa、bb属于同一个矩形 cc、dd属于同一个矩形 相交返回true，不相交返回false
bool Judge(Point aa,Point bb,Point cc,Point dd)
{
//判断两个形成的矩形不相交
if(max(aa.x , bb.x) < min(cc.x , dd.x)) return false;
if(max(aa.y , bb.y) < min(cc.y , dd.y)) return false;
if(max(cc.x , dd.x) < min(aa.x , bb.x)) return false;
if(max(cc.y , dd.y) < min(aa.y , bb.y)) return false;
//现在已经满足快速排斥实验，那么后面就是跨立实验内容(叉积判断两个线段是否相交)
if(mult(aa,cc,bb) * mult(aa,bb,dd) < 0) return false; //正确的话也就是aa,bb要在cc或者dd的两边
if(mult(cc,aa,dd) * mult(cc,dd,bb) < 0) return false;
return true;
}

int main()
{
int n;
while(~scanf("%d",&n))
{
bool flag = true;
for(int i = 0;i < n;i ++)
scanf("%lf%lf%lf%lf",&line[i][0].x,&line[i][0].y,&line[i][1].x,&line[i][1].y);
for(int i = 0;i < n;i ++)
for(int j = i+1;j < n;j ++)
{
if(Judge(line[i][0],line[i][1],line[j][0],line[j][1])) // 判断两条直线是否相交
{
flag = false;
break;
}
if(!flag) break;
}
if(!flag) printf("burned! ");
else printf("ok! ");
}
return 0;
}
参考博客
https://blog.csdn.net/Dacc123/article/details/51219491

https://blog.csdn.net/sizaif/article/details/79192165
---------------------
作者：阿_波_
来源：CSDN
原文：https://blog.csdn.net/li1615882553/article/details/80372202
版权声明：本文为博主原创文章，转载请附上博文链接！

C#代码

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class MathTool : MonoBehaviour
{

    public Transform A, B, C, D;

    // Start is called before the first frame update
    void Start()
    {
        
    }

    // Update is called once per frame
    void Update()
    {
        Debug.Log(IsIntersection0(A.position, B.position, C.position, D.position));
    }

//不优化的情况下
    bool IsIntersection0(Vector3 a, Vector3 b, Vector3 c, Vector3 d)
    {
        Vector3 ca = A.position - C.position;
        Vector3 cb = B.position - C.position;
        Vector3 cd = D.position - C.position;

        Vector3 ba = A.position - B.position;
        Vector3 bc = C.position - B.position;
        Vector3 bd = D.position - B.position;

        Vector3 c1 = Vector3.Cross(ca, cd);
        Vector3 c2 = Vector3.Cross(cd, cb);
        float f1 = Vector3.Dot(c1, c2);

        Vector3 c3 = Vector3.Cross(bc, ba);
        Vector3 c4 = Vector3.Cross(ba, bd);
        float f2 = Vector3.Dot(c3, c4);

        //必须f1，f2同时满足大于等于0才能算相交
        if (f1 >= 0&&f2>=0) return true;
        else return false;
    }
}