认识MATLAB
MATLAB(矩阵实验室)是由美国MathWorks公司开发的第四代高层次的编程语言和交互式环境数值计算,可视化和编程;
MATLAB允许矩阵操作、绘制函数和数据、算法实现、创建用户界面;
MATLAB能和在其他语言,包括C、C++、Java和Fortran语言编写的程序接口;
MATLAB可以分析数据、开发算法、建立模型和应用程序;
MATLAB拥有众多的内置命令和数学函数,可以帮助您在数学计算,绘图和执行数值计算方法。
利用MATLAB计算数学
利用MATLAB计算数学的方方面面。以下是一些常用的数学计算,它最常用于:
-
矩阵和阵列处理
-
2-D和3-D绘图和图形
-
线性代数
-
代数方程组
-
非线性函数
-
统计
-
数据分析
-
微积分和微分方程
-
数值计算
-
积分
-
变换
-
曲线拟合
-
各种其它的特殊功能
MATLAB有什么特点
-
MATLAB可以进行数值计算,可视化和应用程序的开发,这是一个高层次的语言。
-
MATLAB提供了一个互动的环境,探索,设计和解决问题的迭代。
-
MATLAB提供了广阔的线性代数,统计,傅立叶分析,筛选,优化,数值积分,解常微分方程的数学函数库。
-
MATLAB提供了内置的数据可视化工具,用于创建自定义绘制的图形。
-
MATLAB的编程接口给开发工具,提高代码质量和可维护性和性能的最大化。
-
MATLAB提供了自定义的图形界面构建应用程序的工具。
-
MATLAB提供了基于MATLAB算法集成了C,Java,NET和Microsoft Excel等与外部应用程序和语言功能。
MATLAB的用途
MATLAB被广泛用来作为计算工具在科学和工程涵盖领域物理,化学,数学和工程流。它在一定范围内的应用,包括:
- 数值分析
- 数值和符号计算
- 信号处理和通信
- 控制系统的设计与仿真
- 图像和视频处理
- 工程与科学绘图
- 测试和测量
- 财务与金融工程
- 计算生物学
- 管理与调度优化计算(运筹学)
一个简单的MATLAB例子
x = [1 2 3 4 5 6 7 8 9 10];
y1 = [.16 .08 .04 .02 .013 .007 .004 .002 .001 .0008 ];
y2 = [.16 .07 .03 .01 .008 .003 .0008 .0003 .00007 .00002 ];
semilogy(x,y1,'-bo;y1;',x,y2,'-kx;y2;');
title('Plot title');
xlabel('X Axis');
ylabel('Y Axis');
print -deps graph.eps
axis square/将当前坐标系图形设置为方形。横轴及纵轴比例是1:1
axis equal/将横轴纵轴的定标系数设成相同值。
也就是说axis square刻度范围不一定一样,但是一定是方形的。
axis equal刻度是等长的,但也不一定是方形的。
axis EQUAL
使在每个方向的数据单位都相同。其中x-轴、y-轴与z-轴将根据所给数据在各个方向的数据单位自动调整其纵横比,这可以使SPHERE(25) 看起来更像球体,而非椭球体
axis SQUARE
设置当前图形为正方形(或立方体形),系统将调整x-轴、y-轴与z-轴,使它们有相同的长度,同时相应地自动调整数据单位之间的增加量
hold on 是保存axes内图像用的
如果你在新画图像之后不想覆盖原图像就要加上hold on这句话
grid on 是matlab中的一种函数,表示在画图的时候添加网格线。
例如:
例如x=1:10;y=x+2; plot(x,y)执行这样的程序画出的图
matlab命令
第一步常用的系统命令,cd进去指定目录,date显示当前日期,path显示路径,pwd当前目录,type文件的内容,save保存变量等,
这些都是常用的系统命令使用方法,如下图所示:
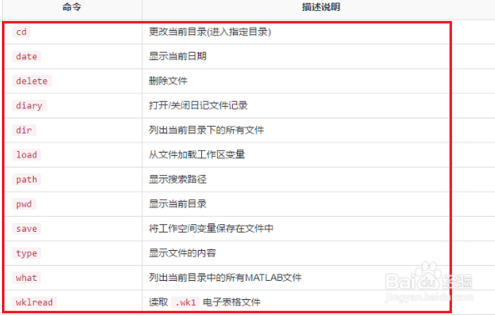
第二步常用的管理会话的命令,clc清除命令行窗口,clear删除变量,exist检查文件是否存在,global声明全局等,如下图所示:

第三步常用的输入输出命令,disp显示字符串或者数组的内容,format格式,input输入,fscanf从文件读取内容等,如下图所示:

第四步其中输入输出命令又包含了一些常用的格式命令,显示为字符串,浮点值,科学记数法等,如下图所示:
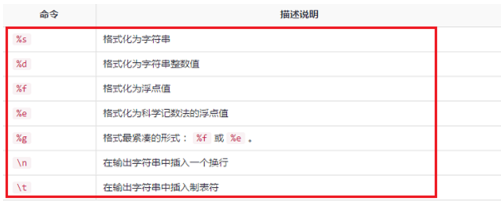
第五步常用的矩阵,向量和数组命令,cat连接数组,max返回最大,min返回最小,size计算数组的大小,sum每列求和等,常用命令使用方法如下图所示:
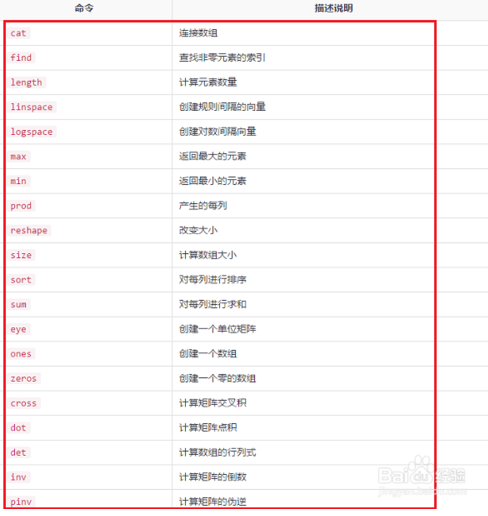
第六步常用的绘图命令,MATLAB比较一个重要的功能就是绘图,
axis,grid,plot,refresh等命令绘图,使用方法如下图所示:
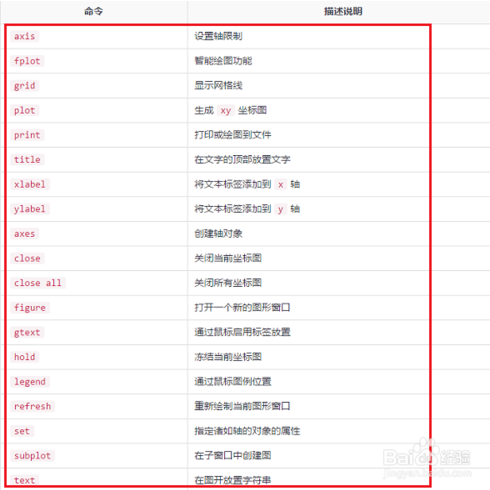
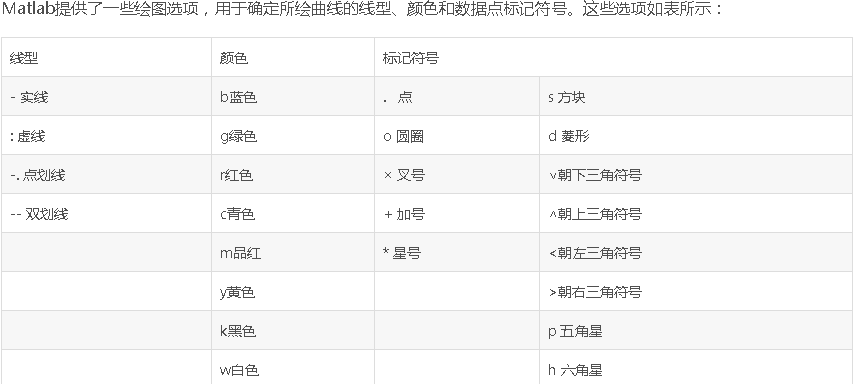
MATLAB在走势图上的颜色设置
MATLAB包含了八个绘制图形的基本颜色选项,下表提供了显示的颜色以及相应的代码:
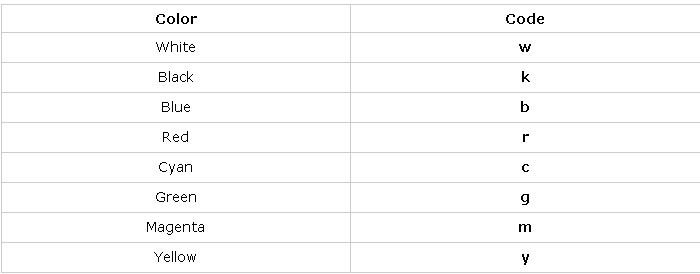
MATLAB绘制条形图
MATLAB 中使用 bar 命令绘制一个二维条形图。
具体示例
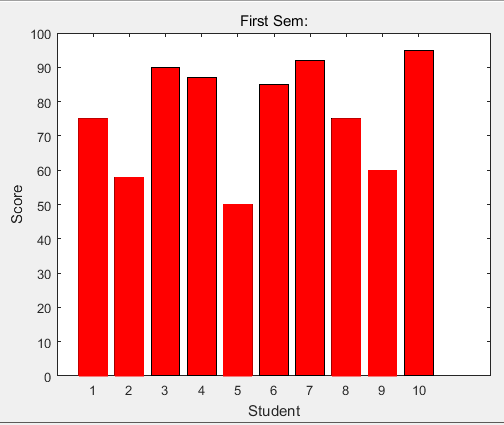
如果有一个包含10名学生的教室,这些学生获得的分数的百分比是75,58,90,87,50,85,92,75,60和95,使用这个数据,我们将绘制条形图。
在MATLAB中建立一个脚本文件,并输入下述代码:
x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps
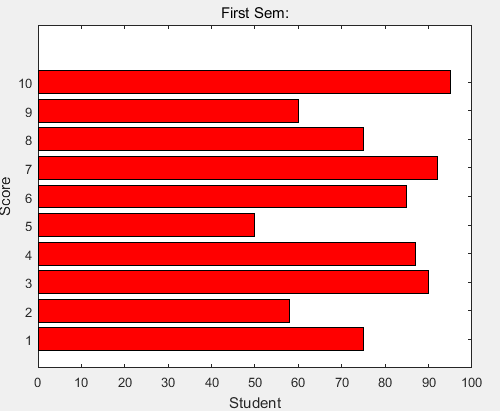
x = [1:10]; y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95]; barh(x,y), xlabel('Student'),ylabel('Score'), title('First Sem:') print -deps graph.eps
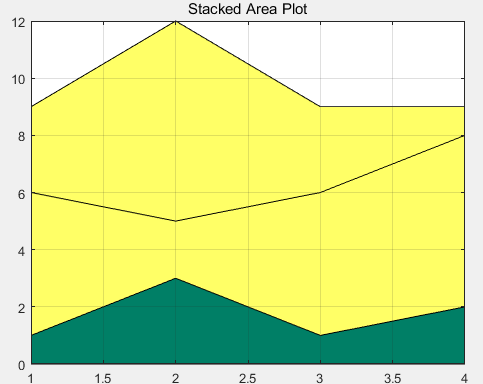
area区域图
Y = [1, 5, 3; 3, 2, 7; 1, 5, 3; 2, 6, 1]; area(Y) grid on colormap summer set(gca,'Layer','top') title 'Stacked Area Plot'
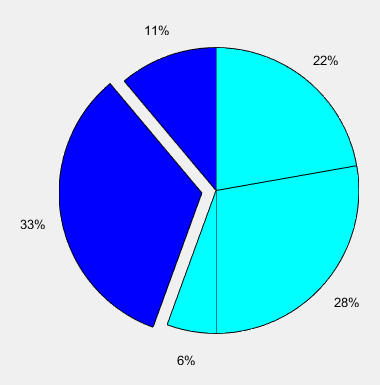
pie函数绘制饼图
x = [1 3 0.5 2.5 2]; explode = [0 1 0 0 0]; pie(x,explode) colormap jet
MATLAB绘制等值线
contour 线的两个变量的函数的曲线,沿着该函数具有一个恒定值。加入等于标高点,一个给定的水平,如平均海平面以上用于创建等高线图等高线。
MATLAB 提供了一个轮廓绘制等高线图的函数。
contour(u,v,z,n)是画等值线 其第四个参数是控制等值线的值的 如果n是一个标量,那么解释为等值线的条数例如 contour(u,v,z,20)那么它会根据数据的范围画出20条等值线 如果n是一个向量,那么解释为需要等值线的值,例如 contour(u,v,z,[1 2 3 4])会画出z=1,2,3,4四个值的等值线 如果我们要只要画指定的某个值的等值线,我们就用两个相同的数组成向量 contour(u,v,z,[1 1]);画值为1的等值线 contour(u,v,z,[0 0]);画值为0的等值线
具体例子
让我们生成的等高线图,显示了对于一个给定的功能的轮廓线 g = f(x, y)。这个函数有两个变量,因此,我们将生成两个独立的变量,即两个数据集 x 和 y。这是通过调用 meshgrid 命令。
meshgrid 命令是用于产生一个矩阵的元素,赋予 x 和 y 的范围内进行了在每一种情况下的增量同规格一起。
让我们绘制函数 g = f(x, y), where −5 ≤ x ≤ 5, −3 ≤ y ≤ 3,这两个值的增量为0.1。这些变量设置语法为:
[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);
最后,我们需要分配功能,函数是:x2 + y2
在 MATLAB 中一个脚本文件,并输入下述代码:
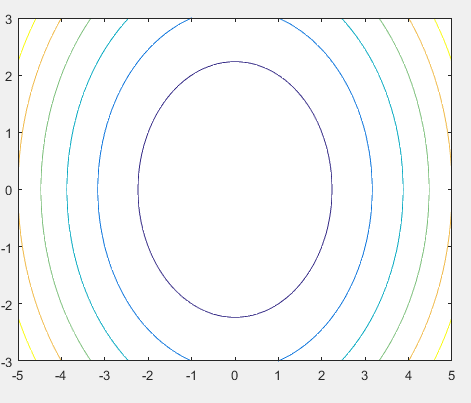
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables g = x.^2 + y.^2; % our function contour(x,y,g) % call the contour function print -deps graph.eps
运行该文件,MATLAB显示的等高线图如下:
让我们修改代码,慢慢美化该等高线图:
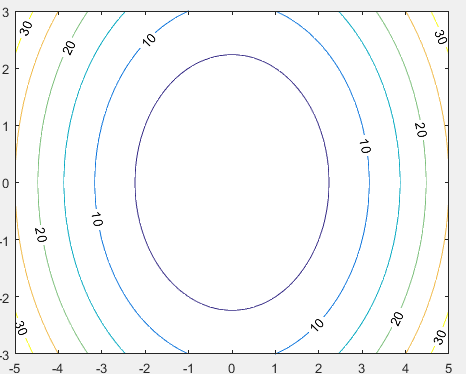
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables g = x.^2 + y.^2; % our function [C, h] = contour(x,y,g); % call the contour function set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2) print -deps graph.eps
运行该文件,MATLAB显示的等高线图变成下述样子:
MATLAB绘制三维图
三维绘图基本显示两个变量中的一个函数定义的表面,g = f (x,y)。
像以前一样,定义 g,我们首先创建一组点(X,Y)函数,使用 meshgrid 命令在域;接下来,我们该函数本身分配;最后使用 surf 命令来创建曲面图。
具体示例
让我们建立一个三维地图函数表面 g = xe-(x2 + y2)
在MATLAB中建立一个脚本文件,并输入下述代码:
[x,y] = meshgrid(-2:.2:2); g = x .* exp(-x.^2 - y.^2); surf(x, y, g) print -deps graph.eps
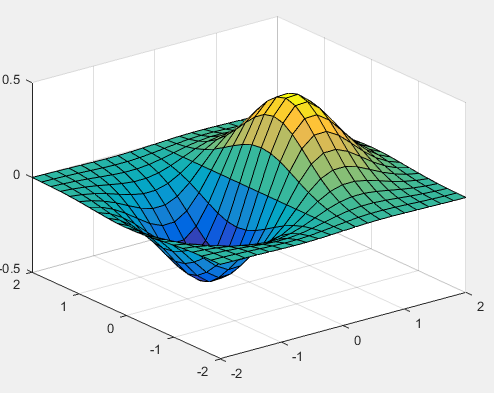
一 . 三维曲线函数:plot3
plot3(X, Y, Z)
plot3(X, Y, Z, S)
plot3(X1, Y1, Z1, S, X2, Y2, Z2, S …)
X、Y和Z:三个方向上的坐标值,尺寸相同
S:对曲线的线型、颜色、线宽、点标记样式等属性进行设置。
当X,Y,Z是同维矩阵时,则以X,Y,Z对应列元素绘制三维曲线,曲
线条数等于矩阵列数。
t = 0:pi/50:10*pi; st = sin(t); ct = cos(t); figure plot3(st,ct,t)
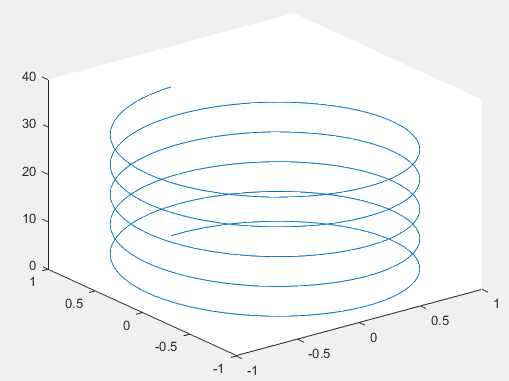
二 . 三维网格图:mesh;
[X,Y] = meshgrid(-8:.5:8); R = sqrt(X.^2 + Y.^2) + eps; Z = sin(R)./R; mesh(Z);
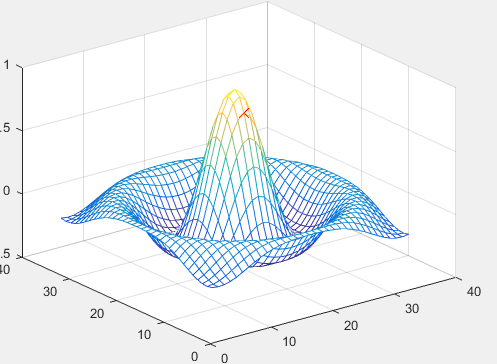
三、曲面图形绘制,surf
曲面图形的绘制使用surf函数完成,与mesh函数类似
surf函数:
k = 5; n = 2^k-1; [x,y,z] = sphere(n); c = hadamard(2^k); surf(x,y,z,c); colormap([1 1 0; 0 1 1]) axis equal
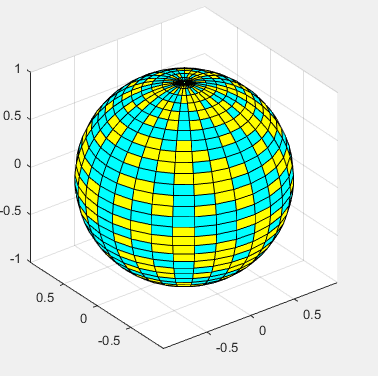
surfc:
> [X,Y,Z] = peaks(30);
surfc(X,Y,Z)
colormap hsv
axis([-3 3 -3 3 -10 10])
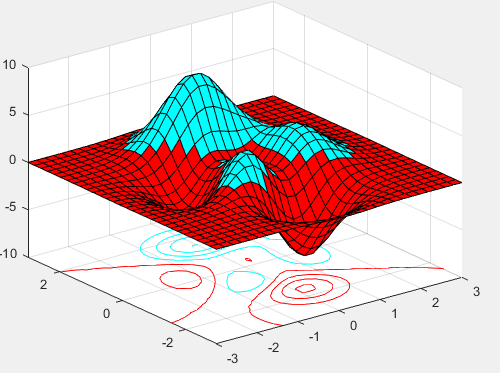
三维曲面实例:
绘制圆锥体![]() 曲面。
曲面。
clc,clear,close all X = -10:1:10; Y = -10:1:10; [X,Y] = meshgrid(X,Y); Z = sqrt(X.^2 + Y.^2); surf(X,Y,Z) xlabel('x') ylabel('y') zlabel('z') box on axis tight colormap(lines) shading interp set(gca,'Ydir','reverse'); set(gcf,'color','w');
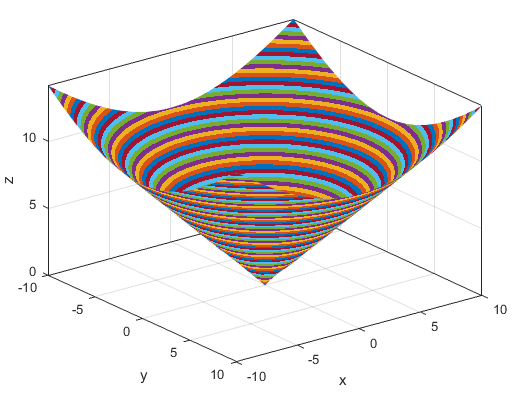
四、特殊图形绘制
Matlab对于不同的三维曲面的绘制提供了不同的画图函数,如slice切片函数、quiver3三维箭头标记函数、sphere等。下面以绘制空间曲线及其运动为例抛砖引玉:
已知空间曲线的方程为:
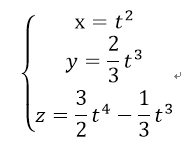
% 空间曲线的绘制 clc,clear,close all t = 00:0.1:1.5; % 设置运动时间 % 给定曲线方程 x = t.^2; y = (2/3)*t.^3; z = (6/4)*t.^4-(1/3)*t.^3; plot3(x,y,x,'r.-'),hold on,grid on % 计算各方向梯度 Vx = gradient(x); Vy = gradient(y); Vz = gradient(z); % 绘制速度矢量图 quiver3(x,y,z,Vx,Vy,Vz); xlabel('x') ylabel('y') zlabel('z')
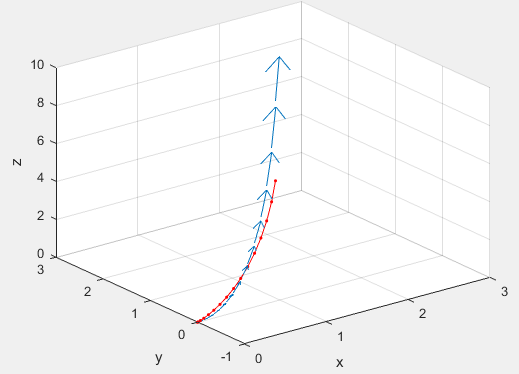
五.三维图形的精细处理
1.视点处理
方位角
Matlab提供了设置视点的函数view,其调用格式为:
view(az,el)
其中az为方位角,el为仰角,它们均以度为单位。系统默认的视点定义为方位角为-37.5度,仰角30度。
实例:从不同视点绘制多峰函数曲面
subplot(2,2,1);mesh(peaks); view(-37.5,30); title('1'); subplot(2,2,2);mesh(peaks); view(0,90); title('2'); subplot(2,2,3);mesh(peaks); view(90,0); title('3'); subplot(2,2,4);mesh(peaks); view(-7,-10); title('4');
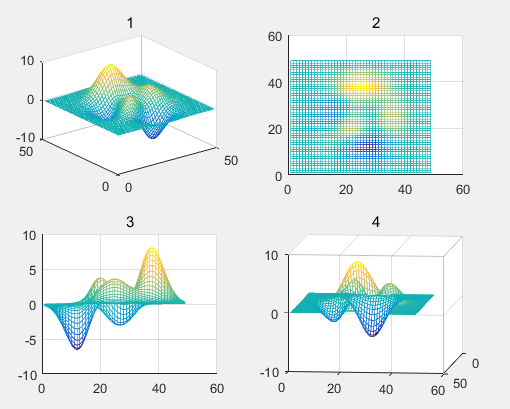
2.色彩处理
3.裁剪处理
六. 动画制作
抖动的帽子
x=-8:0.5:8; [XX,YY]=meshgrid(x); r=sqrt(XX.^2+YY.^2)+eps; Z=sin(r)./r; surf(Z); theAxes=axis; fmat=moviein(20); for j=1:20; surf(sin(2*pi*j/20)*Z,Z) axis(theAxes) fmat(:,j)=getframe; end movie(fmat,10)
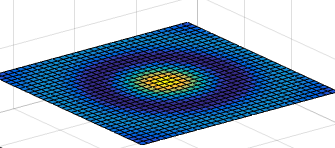

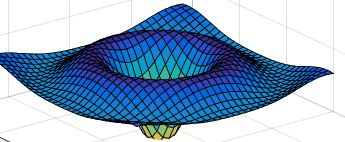
跳动的爱心
figure('Color','y') while 1 for i=-5:0.2:5 f=@(xx,yy,zz) xx.^2.*zz.^3+9*yy.^2.*zz.^3/80-(xx.^2+9*yy.^2/4+zz.^2-1).^3;%心形曲面函数 [xx,yy,zz]=meshgrid(-1.5:0.1:1.5);%画图范围 vv=f(xx,yy,zz); h=patch(isosurface(xx,yy,zz,vv,0)); isonormals(xx,yy,zz,vv,h) set(h,'FaceColor','r','EdgeColor','none'); lighting gouraud view(40*i,20) drawnow axis equal off grid off pause(0.01) end end


