机器学习------线性回归
一、纲要
线性回归的正规方程解法
局部加权线性回归
二、内容详述
1、线性回归的正规方程解法
线性回归是对连续型的数据进行预测。这里讨论的是线性回归的例子,对于非线性回归先不做讨论。这部分内容我们用的是正规方程的解法,理论内容在之前已经解释过了,正规方程为θ = (XT·X)-1·XT·y。值得注意的是这里需要对XT·X求逆矩阵,因此这个方程只有在逆矩阵存在的时候才适用,所以需要在代码中进行判断。
from numpy import *
import matplotlib.pyplot as plt
def loaddataSet(filename):
numfeat = len(open(filename).readline().split(' '))-1
dataMat = [];labelsVec = []
file = open(filename)
for line in file.readlines():
lineArr = []
curLine = line.strip().split(' ')
for i in range(numfeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelsVec.append(float(curLine[-1]))
return dataMat,labelsVec
def standRegression(xArr,yArr):
xMat = mat(xArr);yMat = mat(yArr)
xTx = xMat.T * xMat
if linalg.det(xTx)==0.0:
print('this matrix is singular,cannot do inverse
')
return
sigma = xTx.I * (xMat.T * yMat.T)
return sigma
loaddataSet()函数是将文本数据分成特征集和标签。standRegression()是利用正规方程求回归系数sigma,当然在使用正规方程前需要判断其是否有逆矩阵。这种解法很简单,但是它的缺点我也在之前的理论部分说过了。下面我们来看拟合的结果,利用PlotLine()函数来画图。注意这个函数的传入参数xMay和yMat需要为矩阵形式
def PlotLine(xMat,yMat,sigma):
ax = plt.subplot(111)
ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])
xCopy = xMat.copy()
xCopy.sort(0)
yHat = xCopy*sigma
ax.plot(xCopy[:,1],yHat)
plt.show()
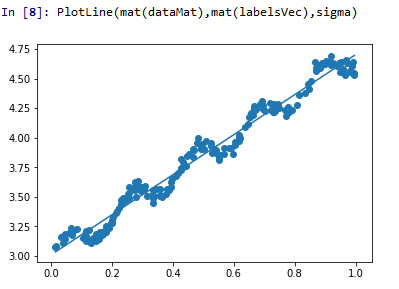
我们得到的拟合直线如图所示,这看起来有点欠拟合的状态。如果用另外一个数据集,得到的拟合直线也是这样的,这也是我们不希望的结果
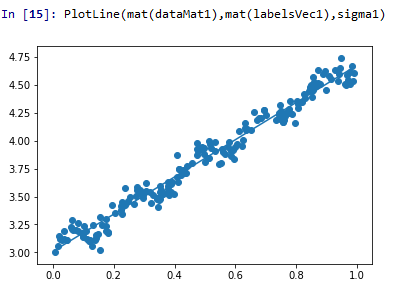
所以,我们后面对该方法进行改进,对回归系数进行局部加权处理。这里的方法叫做局部加权线性回归(LWLR)
2、局部加权线性回归
该算法中,我们给待预测点附近的每个店赋予一定的权重,然后在其上基于最小均方差进行普通的线性回归。其正规方程变为 θ=(XTX)-1XTWy。这里的W为权重。LWLR使用“核”来对附近的点赋予更高的权重,最常用的就是高斯核,其权重为 。这样就构建了只含对角元素的权重矩阵,并且点x与x(i)越近,权重越大。
。这样就构建了只含对角元素的权重矩阵,并且点x与x(i)越近,权重越大。
def lwlr(testPoint,xArr,yArr,k = 1.0):
xMat = mat(xArr);yMat = mat(yArr).T
m = shape(xMat)[0]
weights = mat(eye(m))
for i in range(m):
diffMat = testPoint - xMat[i,:]
weights[i,i] = exp(diffMat * diffMat.T/(-2.0*k**2))
xTWx = xMat.T * (weights*xMat)
if linalg.det(xTWx)==0.0:
print('this matrix is singular,cannot do inverse
')
return
sigma = xTWx.I * (xMat.T * (weights * yMat))
return testPoint * sigma
def lwlrTest(testArr,xArr,yArr,k = 1.0):
m = shape(testArr)[0]
yHat = zeros(m)
for i in range(m):
yHat[i] = lwlr(testArr[i],xArr,yArr,k)
return yHat
lwlr()函数即为局部加权线性回归法的代码,lwlrTest()函数的作用是使lwlr()函数遍历整个数据集。我们同样需要画出图来看拟合结果
def PlotLine1(testArr,xArr,yArr,k = 1.0):
xMat = mat(xArr)
yMat = mat(yArr)
yHat = lwlrTest(testArr,xArr,yArr,k)
srtInd = xMat[:,1].argsort(0)
xsort = xMat[srtInd][:,0,:]
ax = plt.subplot(111)
ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0],s = 2,c = 'red')
ax.plot(xsort[:,1],yHat[srtInd])
plt.show()
当 k=1.0 k=0.01 k=0.003
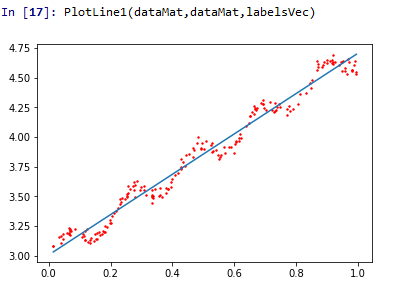
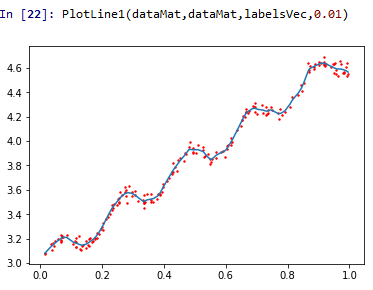
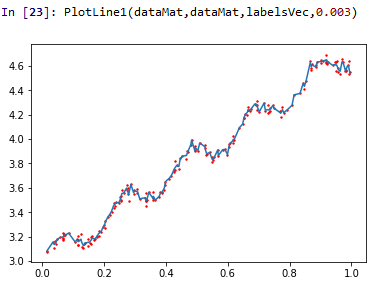
k=1.0就是前面的欠拟合状态,而k=0.003就是过拟合状态了,所以当k=0.01时才是比较好的回归。
数据集和代码下载地址:http://pan.baidu.com/s/1i5AayXn
