这个算法较为简单,主要思想就是给定分好类的数据集,然后将新输入的数据集进入训练集中找到与之最相近的k类,然后将k类所属类别最多的一类作为新数据的分类结果。
注:k的取值对模型拟合效果和预测效果影响较大
其中距离函数有如下表示形式:
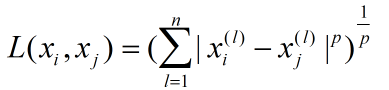
当上式的p为2时,也就是欧式距离;当上式p为1时,也就是曼哈顿距离。当p趋向于无穷大时,该距离是各个坐标距离的最大值。
寻找最多类别的表达式如下:
![]()
其中cj表示该实例的总类别,yi表示每个样本所属类别,I表示指示函数,即当cj=yi时,I为1,否则I为0
但是由于将每个输入样本都与训练数据集进行距离计算会导致计算量过大,因此考虑采用特殊的结构存储来巡检数据,其中就包括kd树。
构造kd树的算法如下:
输入:k维数据集T={x1,x2,...xn} (其中xi=(xi1,xi2,...xik)T ,i=1,2,....n) (k是维度,n是数据的数量)
输出:kd树
(1) 构造根节点,选择以x1为坐标轴,将T数据集中所有数据按照x1坐标的中位数进行切分,将数据集的数据按照x1维大于中位数和小于中位数分为左右2个子结点
(2) 对于深度为j的结点,选取的坐标维度l为:l=j(mod k)+1 ,以该结点的xl作为切分点,将数据集进行切分。
(3) 重复步骤2直到所有数据集分配完毕
以二维数据集T={(2,3)T,(5,4)T,(9,6)T,(4,7)T,(8,1)T,(7,2)T}为例
输出kd树为:

使用kd树的最近邻搜索算法如下:
输入:构造好的kd树,待分析点x
输出:x的最近邻
(1) 从kd树中寻找待分析点的叶结点,若没有相同的叶结,则根据kd树的分类原理往下遍历,直到找到子结点为叶子结点,并标注当前叶子结点为最近结点;
(2) 回退至该子结点的父结点,比较父结点另一子结点与叶结点与待分析点的距离
(3) 若另一子结点距离更小,则将其标注为最近结点, 否则返回父结点的上一层结点,并进行新的结点比较,重复此过程直到返回根节点;