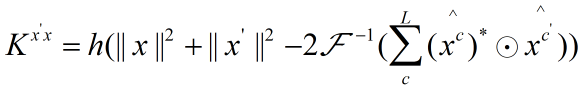KCF跟踪算法

参考：https://www.cnblogs.com/YiXiaoZhou/p/5925019.html

参考：https://blog.csdn.net/shenxiaolu1984/article/details/50884830

 循环矩阵：

KCF里的所有矩阵都是由目标样本循环位移得到，向量的循环可以由排列矩阵得到，如：

为给定向量，通过转换矩阵如：

实现移动：

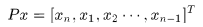
（实现移动的方向为：水平方向的移动）

或者通过如下实现不同方向的移动：

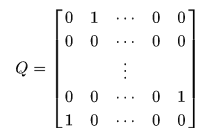
通过xQ来实现移动；

（实现移动的方向为：列方向的移动）

 通过将向量通过不断和排列矩阵相乘得到n个循环位移向量，并将这n个向量一次排序合并到矩阵，则生成了x的循环矩阵，表示为：C(x);

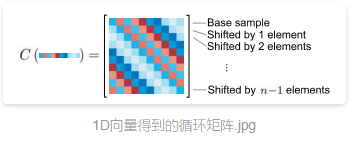
上图为：一维的转换移动

上图为：二维图像的转换移动

如下对在一维情况下进行讨论：

一维脊回归（其实和岭回归一样）：

设训练样本集，那么线性回归函数：，w是列向量表示权重系数，通过最小二乘法求解：

上式也可以写成矩阵形式：

 

其中的每一行x_n表示一个向量，y是列向量，每个元素对应一个样本标签，求解得：

由于后面在傅立叶域内进行计算，涉及到复数矩阵，所以统一写成如下：

其中X^H表示复共轭转置矩阵（共轭的作用在于将a+bi的数转变成a-bi，实数的共轭就是本身，所以这里实数的共轭转置矩阵也等价于实数的转置矩阵）

傅立叶矩阵对角化：

 所有的循环矩阵都可以在傅氏空间中使用离散傅立叶矩阵进行对角化：

 

其中x对应于组成X的向量（也可以理解为第一行矩阵）的傅立叶变化后的值：，也就是傅立叶变换过程；

F是离散傅立叶变换矩阵（DFT matrix），可以用常量表示：

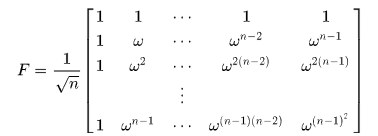
 其中w的表示形式如下（K为方阵F的尺寸，上式用n来表示）：

把w想象成一个角度为2π/K的向量，这个矩阵的每一行是这个向量在不断旋转（？？？）；之所以称为DTF matrix，是因为一个信号的DFT（傅立叶）变换可以通过该矩阵乘积获得：

那么反过来，反傅立叶变换也可以通过类似手段获取：

 

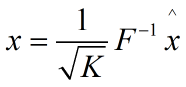
傅立叶矩阵包含许多性质：

 1、对称矩阵

 2、满足，也即酉矩阵；这里可以通过将F^H展开成w^H验证（F代表常数）；

将原公式两边乘以逆矩阵得到：；利用酉矩阵性质，可以获得：

也即矩阵X通过相似变换F变成对角矩阵，从而对循环矩阵X进行对角化；

另外，是矩阵X的2维 DFT变换，即傅立叶变换可以将循环矩阵对角化；

傅氏矩阵对角化的脊回归：

将代入脊回归公式得到：

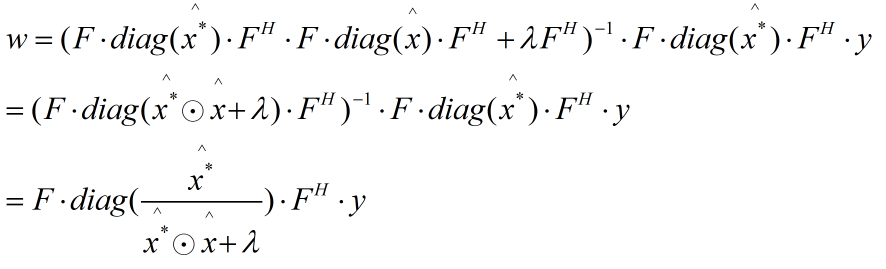
（上式中傅立叶变换后的值右上角带个星号为共轭函数表示）

 由于；所以对如上等式两边同时进行傅立叶变换，得到结果如下：

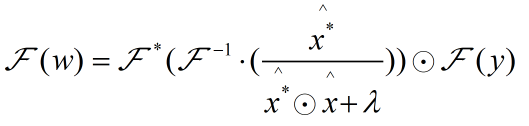
从而得到等式：

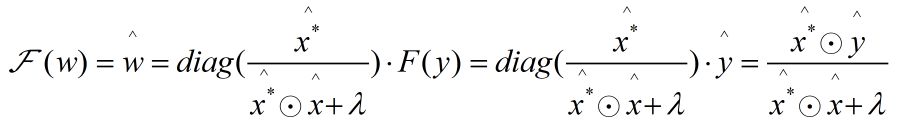
核空间的脊回归：

 通过找到一个非线性映射函数Φ(x)列向量，使映射后的样本在新空间中线性可分；那么再新空间中就可以使用脊回归来寻找一个分类器，这时得到的权重系数w为：

令，由于循环矩阵的非线性转换结果固定，那么如上式子可以转化为求解a的最小：

，这里从求解w转换成求解a，也就是w的对偶问题；

备份一下基础知识：

Y = A * X --> DY/DX = A'
Y = X * A --> DY/DX = A
Y = A' * X * B --> DY/DX = A * B'
Y = A' * X' * B --> DY/DX = B * A'

 令右式为J(a)，那么：

 

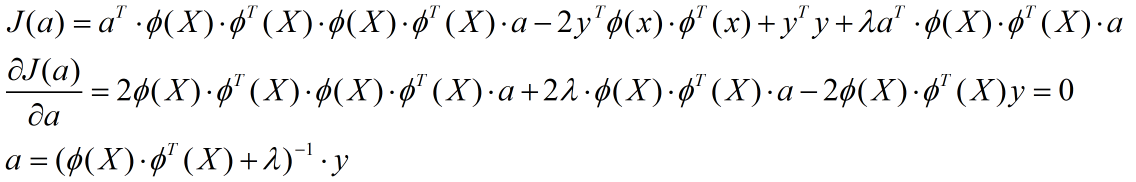
由于类似于核空间变量的协方差矩阵，矩阵和矩阵转置相乘，那么结果一定可逆；

对于核方法，一般不一定知道非线性映射函数Φ(x)的具体形式，只是刻画在核空间的核矩阵，那么令K表示核空间的核矩阵，由核函数得：

;

论文的创新点在于通过循环矩阵对角化简化计算，所以这里如果希望计算a时可以将矩阵求逆运算变为元素运算，就希望将K对角化；故希望找到一个核函数使对应的核矩阵式循环矩阵；

 定理1：若核矩阵K满足：；其中M是排列矩阵，那么为循环矩阵；

证明：设，于是有：

这里将K_ij理解为将第一行的 j-i 个元素放到K的第i行第j列上；

 那么就得到了循环矩阵，所以K是循环矩阵；这里的 j-i 可以理解为除n的余数，这里是循环的；且由于K是循环矩阵，所以有如下表达式：

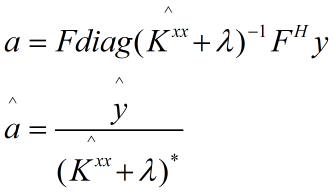
快速检测：

由训练样本和标签训练检测器，其中训练集是由目标区域和位移得到的若干样本组成，对应标签是距离越近正样本可能性越大，从而计算得到a；

待分类样本集，即待检测样本集，是由预测区域和其位移得到的样本集合，这里z是预测区域，z_j是位移样本集；

通过选择最大的样本作为检测出的新目标区域；由z_j判断目标移动的位置；

定义K ^z是测试样本和训练样本间在核空间的核矩阵：

由于这里的K^z满足如下等式：

 ，

所以有K^z为循环矩阵；

 从而得到各测试样本的响应：

 

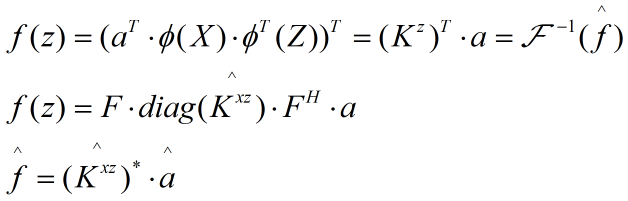
如上的f(z)是列向量；K^xz是矩阵(K^z)^T的第一行，即K^z的第一列；

 K^zx和K^xx都是对称向量，而对称向量的共轭转置是实数；

 核矩阵的快速计算：

 现在存在的矩阵算法就是核矩阵的第一行的计算：

（K的第一行），（K^z的第一列）

内积和多项式核：

这种函数的核矩阵可以表示为：，从而有：

因此对于多项式核有：

径向基核函数：

 比如高斯核，这类函数是的函数：

所以：

对于高斯核则有：

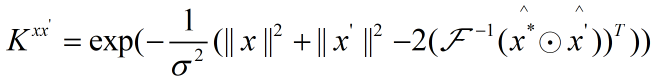
从1维到2维的转换：

 假设是目标图像，M=C(X)是X生成的循环矩阵块；即表示的第(i，j)块，是X右移j，下移i得到的样本块；现有一个函数，自变量，从而在和空间下有如下脊回归公式：

注意：由移动生成的样本共有mn个，所以，这里，是对应样本的标签，Y是对应样本标签的矩阵形式

对于得到的核函数都是块循环矩阵，块循环矩阵可以用2D傅立叶变换矩阵对角化：

上式中的F₂表示2D傅立叶变换矩阵，K^‘表示生成块循环矩阵K的生成矩阵，表示对K^'进行2D傅立叶变换的结果；因此有：

上式的1^m表示全1的m维列向量；

 

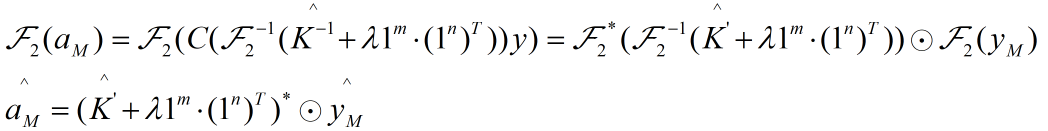
 这里的a_M和y_M分别对应a，y的矩阵形式

 对应预测结果：

 

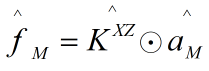
其中K^XZ表示块循环矩阵的生成矩阵；

多通道问题：

Hog特征是将图像划分成较小的局部块，称为cell，在cell里提取梯度信息，绘制梯度方向直方图，为了减少光照影响，将几个cell的方向直方图串在一起进行block归一化，最终将所有的cell直方图串联起来就是图像的特征；

论文的Hog特征提取将sample区域划分为若干个区域，然后将每个区域提取特征，github上给定的代码是在每个区域提取32维特征，即3 x nOrients+5，其中nOrients = 9是梯度方向划分的bin个数，每个方向提取3个特征，其中2个是对方向bin敏感的，1个是不敏感的；另外4个特征是关于表现纹理的特征，最后一个特征为0；提取31个特征（不考虑0）后，将每个cell的特征并起来，那么图像得到的结果就是立方体；假设cell的划分结果为m x n，那么fhog提取的结果就是m x n x 31，称这31个方向为通道；可以通过cell的位移获取样本，这样每一通道对应位置的位移；所有的样本的第 i 通道都是生成图像的第 i 通道位移获得；

 前面提到2维图像的样本cell数为M，每个cell特征维度为L，第 i 个样本的第 j 个通道向量表示为，样本的总特征可以表示为：；

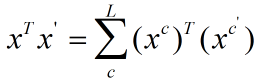
从而K矩阵的第一行有：

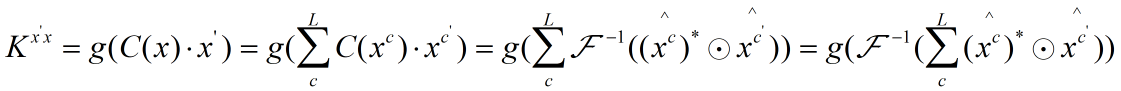
这里涉及到：

这里是核的点乘的结果，所以可以推得径向基核的结果：