机器学习4-分类算法2

朴素贝叶斯算法

朴素

假定特征与特征之间是相互独立的

贝叶斯公式

公式分为三个部分：

• P(C)：每个文档类别的概率(某文档类别数／总文档数量)
• P(W│C)：给定类别下特征（被预测文档中出现的词）的概率P(F1,F2,…) 预测文档中每个词的概率
  • 计算方法：P(F1│C)=Ni/N （训练文档中去计算）
    • Ni为该F1词在C类别所有文档中出现的次数
    • N为所属类别C下的文档所有词出现的次数和

如果计算两个类别概率比较：

 所以我们只要比较前面的大小就可以，得出谁的概率大

有的时候会出现为0的情况，而我们知道为0的情况不大可能出现，因此需要引进另一个参数，防止出现0

拉普拉斯平滑系数

目的：防止计算出的分类概率为0

 

API

• sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
  • 朴素贝叶斯分类
  • alpha：拉普拉斯平滑系数

案例-新闻分类

分析

• 分割数据集

• tfidf进行的特征抽取

• 朴素贝叶斯预测

from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import  MultinomialNB


def nb_news():
    #获取数据集
    news=fetch_20newsgroups(subset="all")
    #划分数据集
    x_train,x_test,y_train,y_test=train_test_split(news.data,news.target)
    #文本特征抽取
    transfer=TfidfVectorizer()
    x_train=transfer.fit_transform(x_train)
    x_test=transfer.transform(x_test)
    #朴素贝叶斯
    estimator=MultinomialNB()
    estimator.fit(x_train,y_train)

    #模型评估
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:
", y_predict)
    print("直接比对真实值和预测值:
", y_test == y_predict)
    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：
", score)



    return None

if __name__ == '__main__':
    nb_news()

结果为：

 

总结

• 优点：
  • 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
  • 对缺失数据不太敏感，算法也比较简单，常用于文本分类。
  • 分类准确度高，速度快
• 缺点：
  • 由于使用了样本属性独立性的假设，所以如果特征属性有关联时其效果不好

决策树

认识决策树

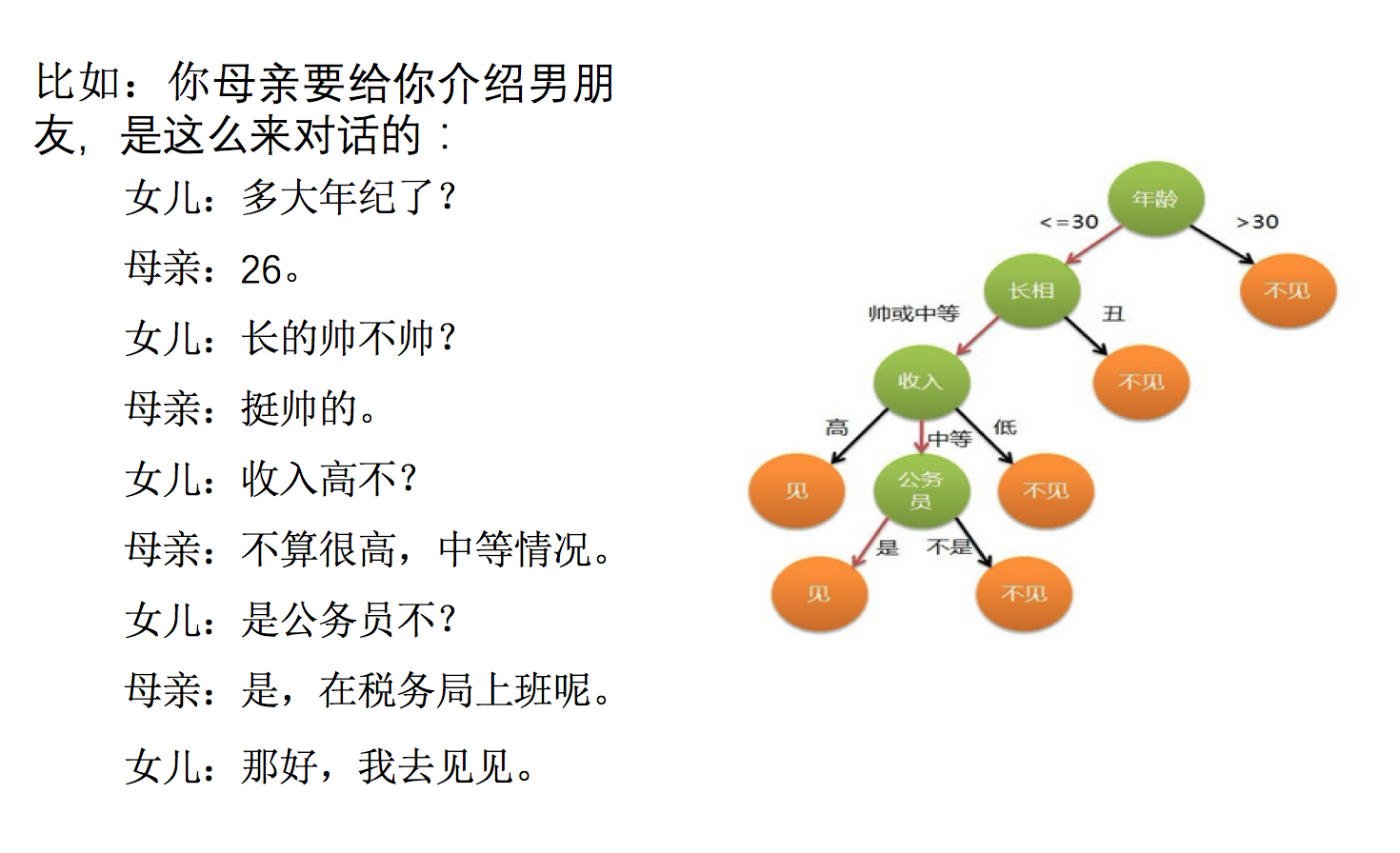
决策树分类原理详解

 

问题：如何对这些客户进行分类预测？你是如何去划分？

有可能你的划分是这样的

 那么我们怎么知道这些特征哪个更好放在最上面，那么决策树的真是划分是这样的

 

原理

信息熵，信息增益

信息熵的定义

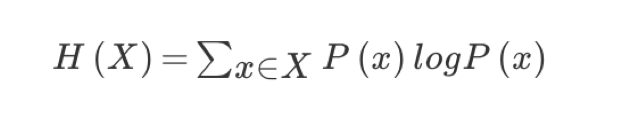
总结（重要）

• 信息和消除不确定性是相联系的

当我们得到的额外信息（球队历史比赛情况等等）越多的话，那么我们猜测的代价越小（猜测的不确定性减小）

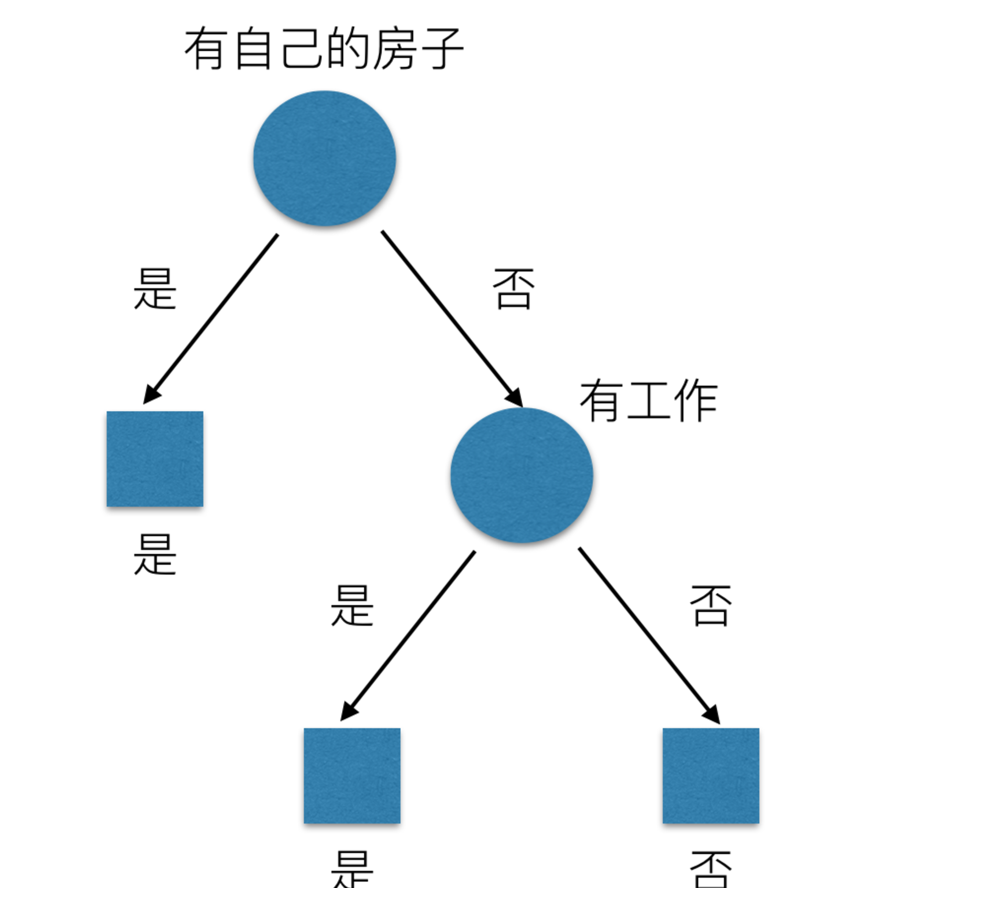
问题： 回到我们前面的贷款案例，怎么去划分？可以利用当得知某个特征（比如是否有房子）之后，我们能够减少的不确定性大小。越大我们可以认为这个特征很重要。那怎么去衡量减少的不确定性大小呢？

决策树的划分依据之一------信息增益

定义与公式

特征A对训练数据集D的信息增益g(D,A),定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差，即公式为：

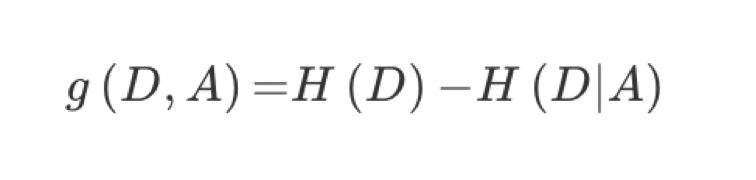
 公式的详细解释：

 

贷款特征重要计算

我们以年龄特征来计算：

1、g(D, 年龄) = H(D) -H(D|年龄) = 0.971-[5/15H(青年)+5/15H(中年)+5/15H(老年]

2、H(D) = -(6/15log(6/15)+9/15log(9/15))=0.971

3、H(青年) = -(3/5log(3/5) +2/5log(2/5))
H(中年)=-(3/5log(3/5) +2/5log(2/5))
H(老年)=-(4/5og(4/5)+1/5log(1/5))

我们以A1、A2、A3、A4代表年龄、有工作、有自己的房子和贷款情况。最终计算的结果g(D, A1) = 0.313, g(D, A2) = 0.324, g(D, A3) = 0.420,g(D, A4) = 0.363。所以我们选择A3 作为划分的第一个特征。这样我们就可以一棵树慢慢建立

决策树API

• class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
  • 决策树分类器
  • criterion:默认是’gini’系数，也可以选择信息增益的熵’entropy’
  • max_depth:树的深度大小
  • random_state:随机数种子
• 其中会有些超参数：max_depth:树的深度大小
  • 其它超参数我们会结合随机森林讲解

案例

鸢尾花决策树分析

from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier,export_graphviz
import pydotplus

def tree():
    """
    用决策树对鸢尾花分类
    """
    #获取数据集
    iris=load_iris()
    #划分数据集
    x_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target,random_state=22)
    #决策树预估器
    estimator=DecisionTreeClassifier(criterion="entropy")
    estimator.fit(x_train,y_train)

    # 模型评估
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:
", y_predict)
    print("直接比对真实值和预测值:
", y_test == y_predict)
    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：
", score)

    #可视化决策树
    dot_data=export_graphviz(estimator,out_file=None,feature_names=iris.feature_names)
    graph = pydotplus.graph_from_dot_data(dot_data)
    graph.write_pdf("iris.pdf")

    return None


if __name__ == '__main__':
    tree()

结果为：

 可视化展示：

泰坦尼克号乘客生存预测

相关数据与说明：https://www.kaggle.com/zephyrzhan522/titanic-prediction-dl-vs-ml

分析

• 选择我们认为重要的几个特征 ['pclass', 'age', 'sex']
• 填充缺失值
• 特征中出现类别符号，需要进行one-hot编码处理(DictVectorizer)数据集划分
  • x.to_dict(orient="records") 需要将数组特征转换成字典数据
• 决策树分类预测

步骤

读取数据

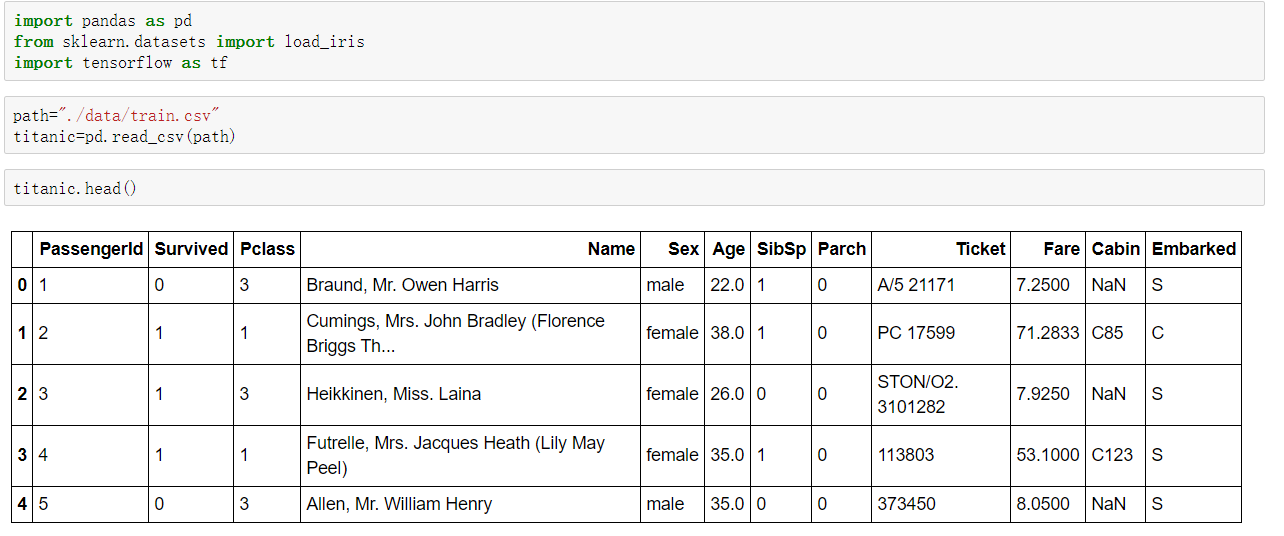
 抽取特征：

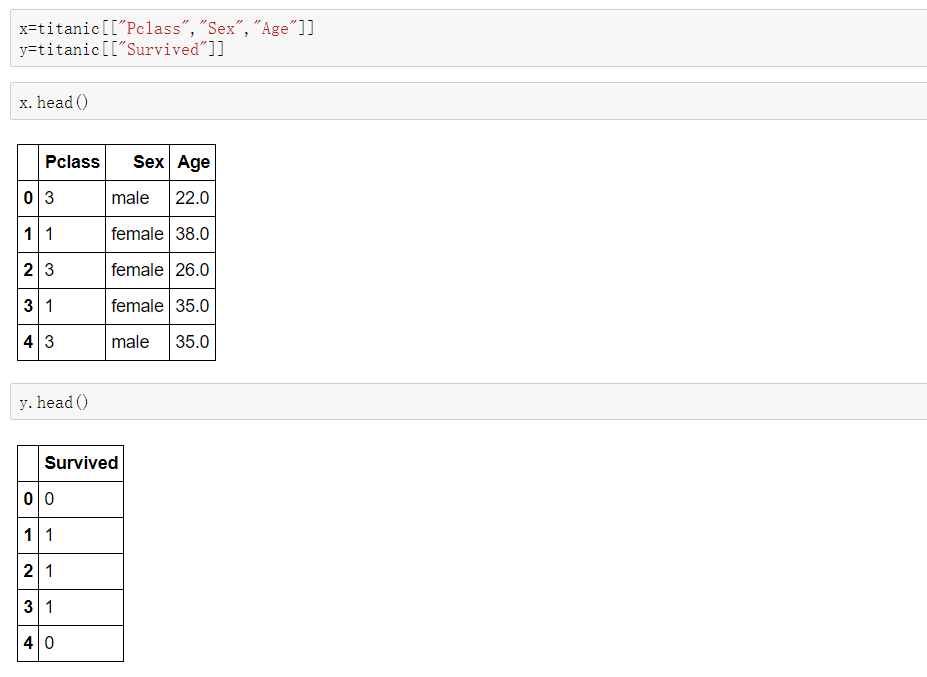
 填充缺失值并转换为字典数据

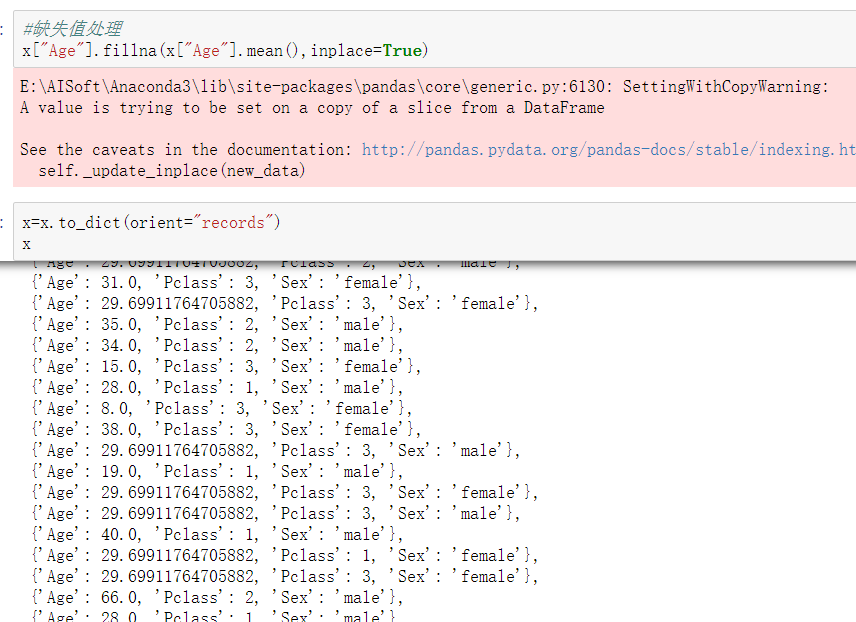
 数据集划分以及相关数据的转化

 决策树预估以及可视化

 

 可视化展示：

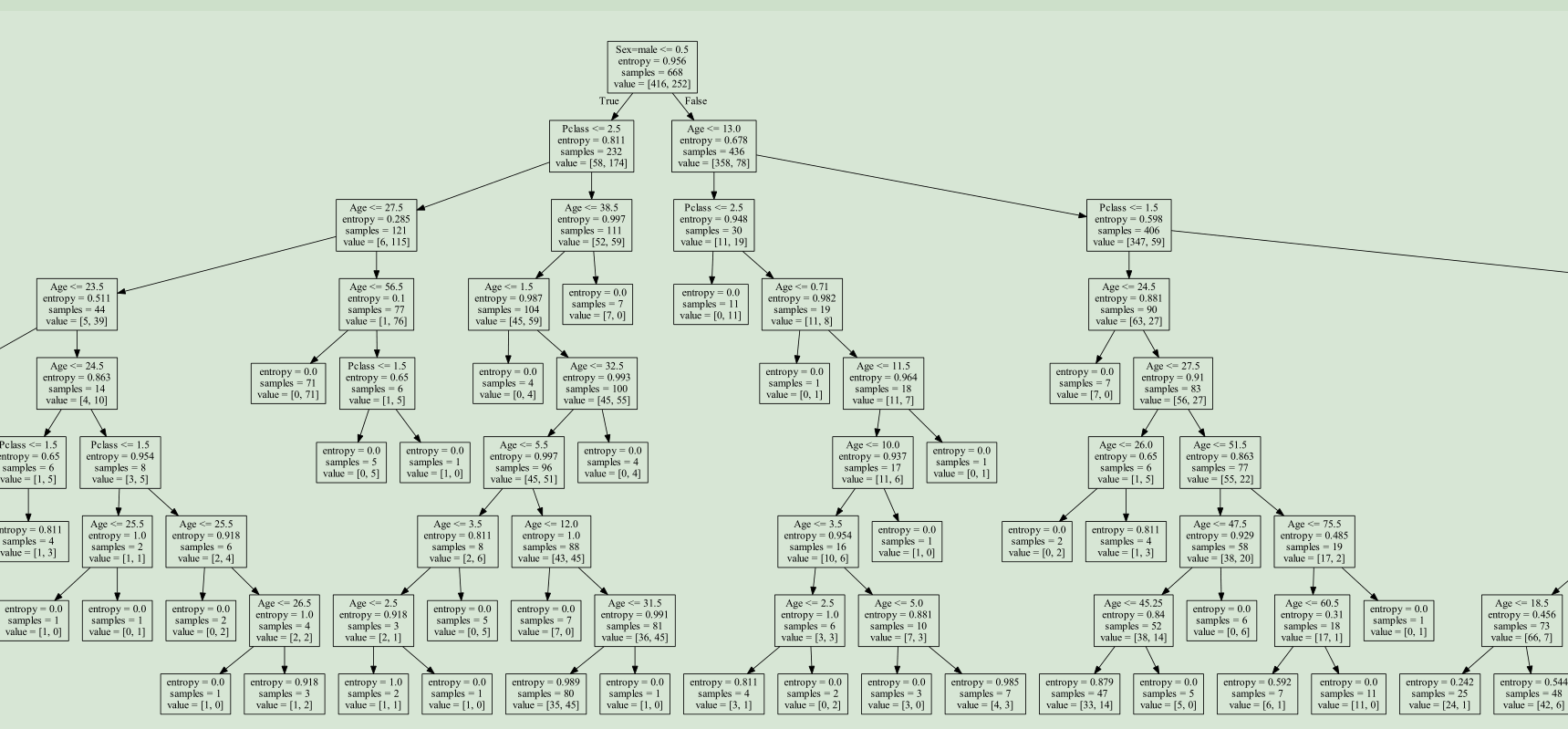
决策树总结

• 优点：
  • 简单的理解和解释，树木可视化。
• 缺点：
  • 决策树学习者可以创建不能很好地推广数据的过于复杂的树，这被称为过拟合。
• 改进：
  • 减枝cart算法(决策树API当中已经实现，随机森林参数调优有相关介绍)
  • 随机森林

注：企业重要决策，由于决策树很好的分析能力，在决策过程应用较多， 可以选择特征

集成学习方法之随机森林

什么是集成学习方法

集成学习通过建立几个模型组合的来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立地学习和作出预测。这些预测最后结合成组合预测，因此优于任何一个单分类的做出预测。

什么是随机森林

随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

例如, 如果你训练了5个树, 其中有4个树的结果是True, 1个数的结果是False, 那么最终投票结果就是True

随机森林原理过程

学习算法根据下列算法而建造每棵树：

• 用N来表示训练用例（样本）的个数，M表示特征数目。采取bootstrap抽样
  • 1、一次随机选出一个样本，重复N次， （有可能出现重复的样本）
  • 2、随机去选出m个特征, m <<M，建立决策树

为什么采用BootStrap抽样

• 为什么要随机抽样训练集？　　
  • 如果不进行随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的
• 为什么要有放回地抽样？
  • 如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是“有偏的”，都是绝对“片面的”（当然这样说可能不对），也就是说每棵树训练出来都是有很大的差异的；而随机森林最后分类取决于多棵树（弱分类器）的投票表决。

API

• class sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)

  • 随机森林分类器
  • n_estimators：integer，optional（default = 10）森林里的树木数量120,200,300,500,800,1200
  • criteria：string，可选（default =“gini”）分割特征的测量方法
  • max_depth：integer或None，可选（默认=无）树的最大深度 5,8,15,25,30
  • max_features="auto”,每个决策树的最大特征数量
    • If "auto", then max_features=sqrt(n_features).
    • If "sqrt", then max_features=sqrt(n_features) (same as "auto").
    • If "log2", then max_features=log2(n_features).
    • If None, then max_features=n_features.
  • bootstrap：boolean，optional（default = True）是否在构建树时使用放回抽样
  • min_samples_split:节点划分最少样本数
  • min_samples_leaf:叶子节点的最小样本数

• 超参数：n_estimator, max_depth, min_samples_split,min_samples_leaf

案例

还是刚刚的泰坦尼克号，用随机森林进行预测

结果为：

总结

• 在当前所有算法中，具有极好的准确率
• 能够有效地运行在大数据集上，处理具有高维特征的输入样本，而且不需要降维
• 能够评估各个特征在分类问题上的重要性

分类算法总结