❤️图的遍历❤️

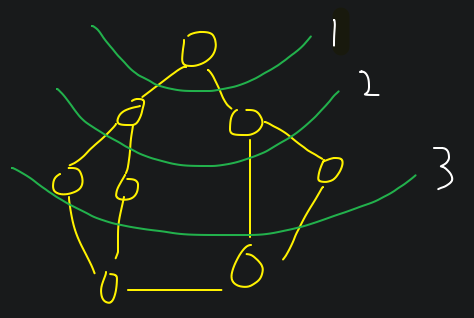
广度优先搜索

'广搜':以v为起始点，由近至远依次访问和v路径想通且路径长度为1,2,...的顶点
'广搜'是一种分层的查找过程
时间复杂度 O(n+m)

空间复杂度 O(n)（vis 数组和队列）
算法过程可以看做是图上'火苗传播的过程'：最开始只有起点着火了，在每一时刻，有火的节点都向它相邻的所有节点传播火苗。

void bfs(int u) {
  while (!Q.empty()) Q.pop();
  Q.push(u);
  vis[u] = 1;
  d[u] = 0;
  p[u] = -1;
  while (!Q.empty()) {
    u = Q.front();
    Q.pop();
    for (int i = head[u]; i; i = e[i].x) {
      if (!vis[e[i].t]) {
        Q.push(e[i].t);
        vis[e[i].t] = 1;
        d[e[i].t] = d[u] + 1;
        p[e[i].t] = u;
      }
    }
  }
}
void restore(int x) {
  vector<int> res;
  for (int v = x; v != -1; v = p[v]) {
    res.push_back(v);
  }
  std::reverse(res.begin(), res.end());
  for (int i = 0; i < res.size(); ++i) printf("%d", res[i]);
  puts("");
}

广度伪代码

bfs(s) {
  q = new queue()
  q.push(s), visited[s] = true
  while (!q.empty()) {
    u = q.pop()
    for each edge(u, v) {
      if (!visited[v]) {
        q.push(v)
        visited[v] = true
      }
    }
  }
}

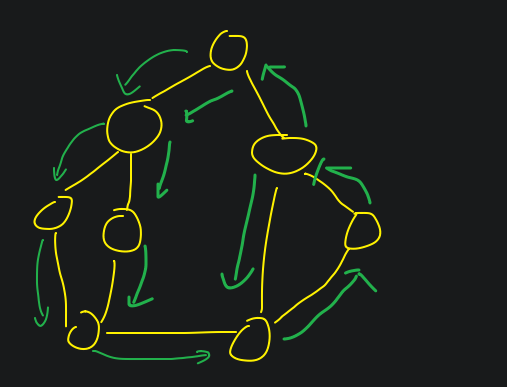
深度优先搜索

所谓'深度优先'，就是说每次都尝试向'更深的节点走'
DFS 最显著的特征在于其 递归调用自身 。同时与 BFS 类似，DFS 会对其访问过的点打上'访问标记'，
在遍历图时跳过已打过标记的点，以确保 每个点仅访问一次 
'时间复杂度' O(n+m)

'空间复杂度' O(n)
其中 n 表示点数,m表示边数,复杂度包含了栈空间，栈空间的空间复杂度是 O(n)

void dfs(int u) {
  vis[u] = 1;
  for (int i = head[u]; i; i = e[i].x) {
    if (!vis[e[i].t]) {
      dfs(v);
    }
  }
}