❤️排序❤️

插入排序

插入排序

每次将一个待排序的记录按其关键字大小'插入'到前面'已排好序的子序列中'，类似于扑克牌的插入
例如 n=6，数组R的六个排序码分别为：17，3，25，14，20，9。它的直接插入排序的执行过程

void InsertSort(ElemType A[],int n){
    int i,j;
    for(i=2; i<=n; i++){
        if(A[i] < A[i-1]){
            A[0] = A[i];    //复制给哨兵，A[0]不存元素
            for(j=i-1; A[0]<A[i]; --j){
                A[j+1] = A[j];      //向后移动
            }
            A[j+1] = A[0];      //复制到插入位置
        }
    }
}

希尔排序

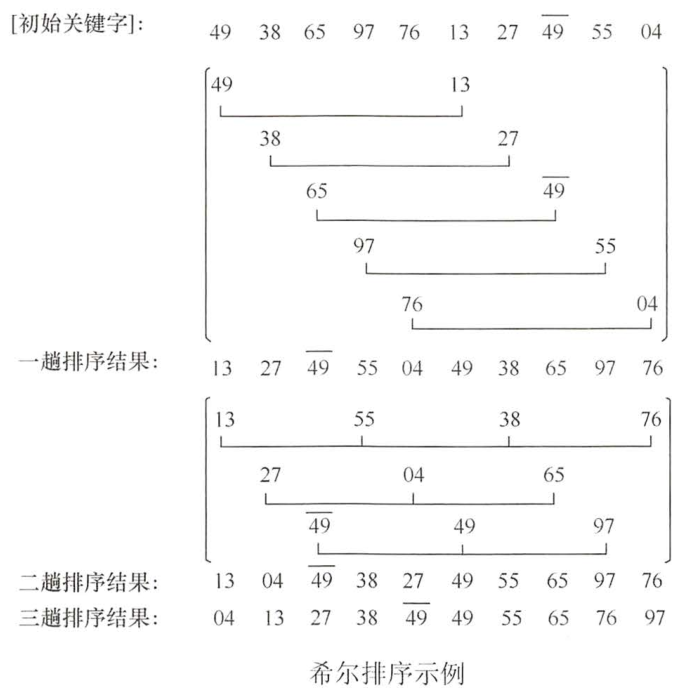
先将整个待排序的记录序列分割成为若干子序列分别进行'直接插入排序'，待整个序列中的记录“基本有序”时，
再对全体记录进行依次直接插入排序。假设增量为5，则i,i+5....;下图增量为5

void ShellSort(ElemType A[],int n){
    //A[0]用来暂存单元
    for(i=dk+1; dk>=1; dk=dk/2){    //步长变化
        for(i=id+1; i<=n; i++){
            if(A[i] < A[i-dk]){     //需将A[i]插入有序增量表
                A[0] = A[i];        //暂存在A[0]
                for(j=i-dk; j>0&&A[0]<A[j]; j-=dk){
                    //记录后移，查找插入的位置
                    A[j+dk] = A[j];     
                }
                A[j+dk] = A[0]      //插入
            }
        }
    }
}

交换排序

冒泡排序

对待排序序列从后向前（从下标较大的元素开始），'依次比较相邻元素'的排序码，若发现'逆序则交换'，
使排序码较小的元素逐渐从后部移向前部，就象水底下的气泡一样逐渐向上冒。
例如，n=6，数组R的六个排序码分别为：17，3，25，14，20，9。下面图给出冒泡排序算法的执行过程。

void BubbleSort(ElemType A[],int n){
    for(i=0; i<n-1; i++){
        flag = false;   //表示本趟冒泡是否发生交换
        for(j=n-1; j<i; j--){   //一趟冒泡过程
            if(A[j-1] > A[j]){
                swap(A[j-1],A[i]);  //交换
                flag = true;
            }
            if(flag == false){
                 //表示遍历后没有发生交换，说明表已有序
                return;    
            }
        }
    }
}

快速排序

基本思想是：取待排序序列中的某个元素（一般第一个元素）作为基准，通过一趟排序，将待排元素分为'左右两个子序列'，
'左子序列元素'的排序码均'小于或等于基准元素'的排序码，
'右子序列'的排序码则'大于基准元素'的排序码，
然后分别对两个子序列继续进行快速排序，直至整个序列有序。
元素的比较和交换是从两端向中间进行的，排序码较大的元素一次就能够交换到后面，排序码较小的记录一次就能够交换到前面，
记录每次移动的距离较远，因而总的比较和移动次数较少。
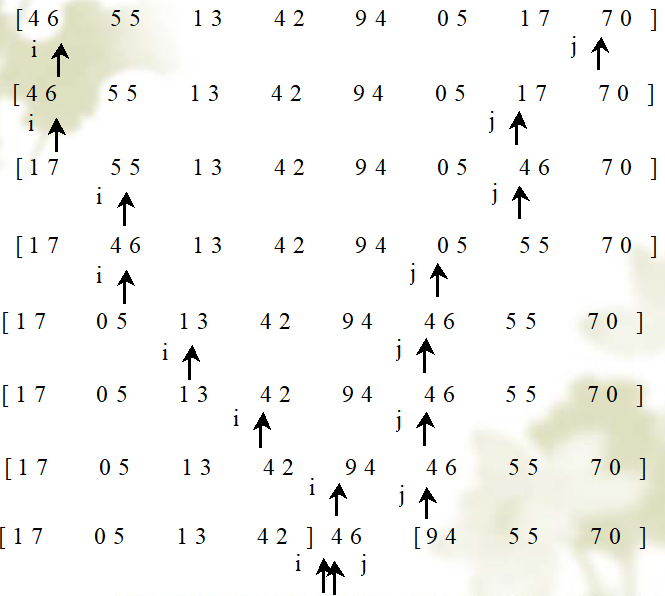
例如，给定排序码为：'（46，55，13，42，94，05，17，70）'

一次划分

void QuickSort(ElemType A[],int low,int high){
    if(low < high){
        /*
        Partition()就是划分操作，将A[low....high]
        划分为满族上述条件的两个子表
        */
       int pivotpos = Partition(A,low,high);    //划分
       QuickSort(A,low,pivotpos-1);    //依次对两个子表进行递归排序
       QuickSort(A,pivotpos+1,high);    
    }
}

int Partition(ElemType A[],int low,int high){
    //一次划分
    ElemType pivot = A[low];    //将当前表中第一个元素设为轴，对表进行划分
    while(low < high){
        while(low<high && A[low]>=pivot){
            --high;
        }
        A[low] = A[high];   //将比轴小的元素移动到左端
        while(low<high && A[low]<=pivot){
            ++low;
        }
        A[high] = A[low];   //将比轴大的元素移动到右端
    }
    A[low] = pivot; //将轴元素放到最终位置
    return low;     //返回存放轴饿最终位置
}

选择排序

简单选择排序

基本思想是：第一次从'array[0]~array[n-1]'中'选取最小值'，与'array[0]'交换，
第二次从'array[1]~array[n-1]'中选取最小值，与'array[1]'交换，
第三次从'array[2]~array[n-1]'中选取最小值，与'array[2]'交换，…
例如，给定n=8，数组R中的8个元素的排序码为：'（8，3，2，1，7，4，6，5）'

void SelectSort(ElemType A[],int n){
    for(i=0; i<n-1; i++){
        //一共进行n-1趟
        min = i;    //记录最小元素位置
        for(j=i+1; j<n; j++){   //找最小元素
            if(A[j] < A[min]){
                min = j;    //更新最小元素的位置
            }
            if(min != j){
                swap(A[i],A[min]);  //交换
            }
        }
    }
}

堆排序

将排序码k1，k2，k3，…，kn表示成'一棵完全二叉树'，然后从第n/ 个排序码(即树的最后一个非叶结点)开始筛选，
使由该结点作根结点组成的子二叉树符合堆的定义，然后从第n/2 -1个排序码重复刚才操作，直到第一个排序码止。
这时候，该二叉树符合堆的定义，初始堆已经建立。 
可以按如下方法进行堆排序：将堆中第一个结点（二叉树根结点）和最后一个结点的数据进行交换（k1与kn），
再将k1~kn-1重新建堆，然后k1和kn-1交换，再将k1~kn-2重新建堆，然后k1和kn-2交换，如此重复下去，
每次重新建堆的元素个数不断减1，直到重新建堆的元素个数仅剩一个为止。

void BuildMaxHeap(ElemType A[],int len){
    for(i=len/2; i>0; i--){     //从i=[n/2]~1,反复调整堆
        HeadAdjust(A,i,len);    
    }
}

void HeadAdjust(ElemType A[],int k,int len){
    A[0] = A[k];    //A[0]暂存子树的根节点
    for(i=2*k; i<=len; i*=2){   //沿key较大的子节点向下筛选
        if(i<len && A[i]<A[i+1]){
            i++;    //去key较大的子节点的下标
        }
        if(A[0] >= A[i])    break;  //筛选结束
        else{
            A[k] = A[i];    //将A[i]调整到双亲结点
            k = i;  //修改k值，以便继续向下筛选
        }
    }
    A[k] = A[0];    //被筛选节点的值的最终位置
}

归并排序

将两个（或两个以上）有序表合并成一个'新的有序表'，即把待排序序列'分为若干个子序列'，每个子序列是'有序的'。然后再把有序子序列合并为整体有序序列。

//辅助数组B
ElemType *B=(ElemType*)malloc((n+1)*sizeof(ElemType));

void Merge(ElemType A[],int low,int mid,int high){
    //表A的两段A[low...mid]和A[mid+1...high]各自有序，将他们合并成一个有序表
    for(k=low; k<=high; k++){
        B[k] = A[k];    //将A中的所有元素复制到B中
    }
    for(i=low,j=mid+1,k=i; i<=mid&&j<=high; k++){
        if(B[i] <= B[j]){   //比较B的左右两段中的元素
            A[k] = B[i++];  //将较小值复制到A中
        }else{
            A[k] = B[j++];
        }   
    }
    while (i<=mid) A[k++] =B [i++]; //若第一个表未检测完，进行复制
    while (i<=mid) A[k++] =B [j++]; //若第二个表未检测完，进行复制   
}

void MergeSort(ElemType A[],int low,int high){
    if (low<high){
        int mid=(low+high)/2;   //从中间划分两个子序列
        MergeSort(A ,low,mid);  //对左子序列进行递归排序
        MergeSort(A ,mid+1,high);  //对右子序列进行递归排序
        Merge(A,low,mid，high);  //归并        
    }
}

基数排序

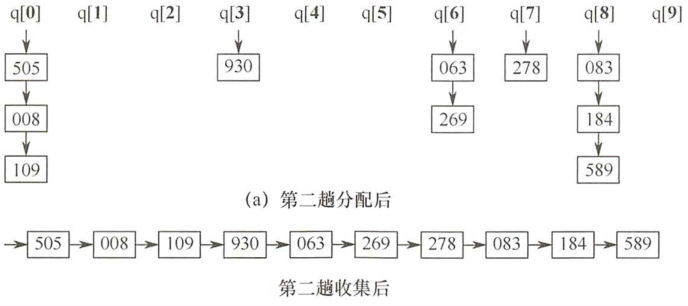
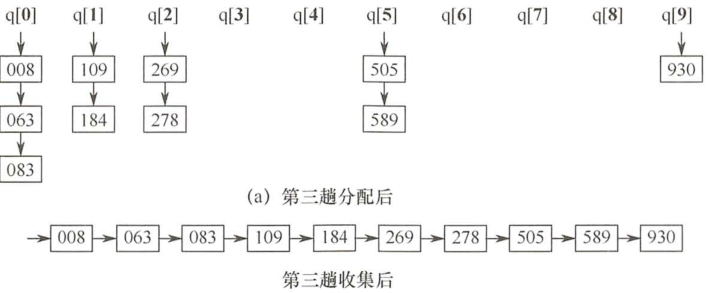
数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，
它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，
基数排序法是属于稳定性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

各个排序比较

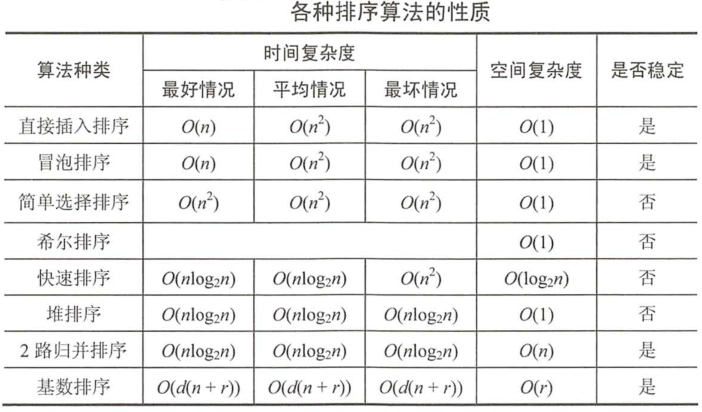
'不稳定'：'快选堆希'（快速排序、选择排序、堆排序、希尔排序）
'稳定'：'插冒归计基'（简单插入排序、冒泡排序、归并排序、计数排序、基数排序）
移动次数和关键字顺序无关的排序：
'一堆（堆排序）海龟（归并排序）选（选择排序）基（基数排序）友'--->'堆排序、归并排序、选择排序、基数排序'

败者树balabala.. 不想写了 写吐了

部分图片来自王道数据结构书中