2-3 查找树
定义(来源:wiki)
2–3树是一种树型数据结构,内部节点(存在子节点的节点)要么有2个孩子和1个数据元素,要么有3个孩子和2个数据元素,叶子节点没有孩子,并且有1个或2个数据元素。


-
定义
如果一个内部节点拥有一个数据元素、两个子节点,则此节点为2节点。
如果一个内部节点拥有两个数据元素、三个子节点,则此节点为3节点。
当且仅当以下叙述中有一条成立时,T为2–3树:
- T为空。即T不包含任何节点。
- T为拥有数据元素a的2节点。若T的左孩子为L、右孩子为R,则
- L和R是等高的非空2–3树;
- a大于L中的所有数据元素;
- a小于等于R中的所有数据元素。
- T为拥有数据元素a和b的3节点,其中a < b。若T的左孩子为L、中孩子为M、右孩子为R,则
- L、M、和R是等高的非空2–3树;
- a大于L中的所有数据元素,并且小于等于M中的所有数据元素;
- b大于M中的所有数据元素,并且小于等于R中的所有数据元素。
查找
首先我们说一下查找
2-3查找树的查找和二叉树很类似,无非就是进行比较然后选择下一个查找的方向。 (这几张图不知道来源,知道的呲我一声)

插入
2-3查找树的插入
我们可以思考一下,为什么要两个结点。在前面可以知道,二叉查找树变成链表的原因就是因为新插入的结点没有选择的”权利”,当我们插入一个元素的时候,实际上它的位置已经确定了, 我们并不能对它进行操作。那么2-3查找树是怎么做到赋予“权利”的呢?秘密便是这个多出来结点,他可以缓存新插入的结点。(具体我们将在插入的时候讲)
前面我们知道,2-3查找树分为2结点和3结点,so,插入就分为了2结点插入和3结点插入。
**2-结点插入:**向2-结点插入一个新的结点和向而插入插入一个结点很类似,但是我们并不是将结点“吊”在结点的末尾,因为这样就没办法保持树的平衡。我们可以将2-结点替换成3-结点即可,将其中的键插入这个3-结点即可。(相当于缓存了这个结点)

3-结点插入: 3结点插入比较麻烦,emm可以说是特别麻烦,它分为3种情况。
-
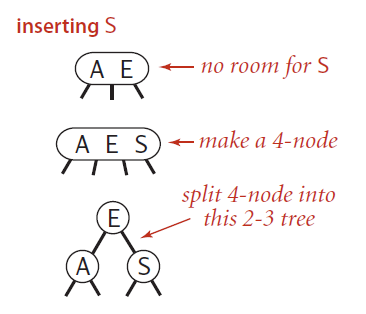
向一棵只含有3-结点的树插入新键。
假如2-3树只有一个3-结点,那么当我们插入一个新的结点的时候,我们先假设结点变成了4-结点,然后使得中间的结点为根结点,左边的结点为其左结点,右边的结点为其右结点,然后构成一棵2-3树,树的高度加1。
-
向父结点为2-结点的3-结点中插入新键。
和上面的情况类似,我们将新的节点插入3-结点使之成为4-结点,然后将结点中的中间结点”升“到其父节点(2-结点)中的合适的位置,使其父节点成为一个3-节点,然后将左右节点分别挂在这个3-结点的恰当位置,树的高度不发生改变

-
向父节点为3-结点的3-结点中插入新键。
这种情况有点类似递归:当我们的结点为3-结点的时候,我们插入新的结点会将中间的元素”升“父节点,然后父节点为4-结点,右将中间的结点”升“到其父结点的父结点,……如此进行递归操作,直到遇到的结点不再是3-结点。

JAVA代码实现2-3树
接下来就是最难的操作来了,实现这个算法,2-3查找树的算法比较麻烦,所以我们不得不将问题分割,分割求解能将问题变得简单。参考博客
接下来就是最难的操作来了,实现这个算法,2-3查找树的算法比较麻烦,所以我们不得不将问题分割,分割求解能将问题变得简单。参考博客
首先我们定义数据结构,作用在注释已经写的很清楚了。
public class Tree23<Key extends Comparable<Key>,Value> {
/**
* 保存key和value的键值对
* @param <Key>
* @param <Value>
*/
private class Data<Key extends Comparable<Key>,Value>{
private Key key;
private Value value;
public Data(Key key, Value value) {
this.key = key;
this.value = value;
}
public void displayData(){
System.out.println("/" + key+"---"+value);
}
}
/**
* 保存树结点的类
* @param <Key>
* @param <Value>
*/
private class Node23<Key extends Comparable<Key>,Value>{
public void displayNode() {
for(int i = 0; i < itemNum; i++){
itemDatas[i].displayData();
}
System.out.println("/");
}
private static final int N = 3;
// 该结点的父节点
private Node23 parent;
// 子节点,子节点有3个,分别是左子节点,中间子节点和右子节点
private Node23[] chirldNodes = new Node23[N];
// 代表结点保存的数据(为一个或者两个)
private Data[] itemDatas = new Data[N - 1];
// 结点保存的数据个数
private int itemNum = 0;
/**
* 判断是否是叶子结点
* @return
*/
private boolean isLeaf(){
// 假如不是叶子结点。必有左子树(可以想一想为什么?)
return chirldNodes[0] == null;
}
/**
* 判断结点储存数据是否满了
* (也就是是否存了两个键值对)
* @return
*/
private boolean isFull(){
return itemNum == N-1;
}
/**
* 返回该节点的父节点
* @return
*/
private Node23 getParent(){
return this.parent;
}
/**
* 将子节点连接
* @param index 连接的位置(左子树,中子树,还是右子树)
* @param child
*/
private void connectChild(int index,Node23 child){
chirldNodes[index] = child;
if (child != null){
child.parent = this;
}
}
/**
* 解除该节点和某个结点之间的连接
* @param index 解除链接的位置
* @return
*/
private Node23 disconnectChild(int index){
Node23 temp = chirldNodes[index];
chirldNodes[index] = null;
return temp;
}
/**
* 获取结点左或右的键值对
* @param index 0为左,1为右
* @return
*/
private Data getData(int index){
return itemDatas[index];
}
/**
* 获得某个位置的子树
* @param index 0为左指数,1为中子树,2为右子树
* @return
*/
private Node23 getChild(int index){
return chirldNodes[index];
}
/**
* @return 返回结点中键值对的数量,空则返回-1
*/
public int getItemNum(){
return itemNum;
}
/**
* 寻找key在结点的位置
* @param key
* @return 结点没有key则放回-1
*/
private int findItem(Key key){
for (int i = 0; i < itemNum; i++) {
if (itemDatas[i] == null){
break;
}else if (itemDatas[i].key.compareTo(key) == 0){
return i;
}
}
return -1;
}
/**
* 向结点插入键值对:前提是结点未满
* @param data
* @return 返回插入的位置 0或则1
*/
private int insertData(Data data){
itemNum ++;
for (int i = N -2; i >= 0 ; i--) {
if (itemDatas[i] == null){
continue;
}else{
if (data.key.compareTo(itemDatas[i].key)<0){
itemDatas[i+1] = itemDatas[i];
}else{
itemDatas[i+1] = data;
return i+1;
}
}
}
itemDatas[0] = data;
return 0;
}
/**
* 移除最后一个键值对(也就是有右边的键值对则移右边的,没有则移左边的)
* @return 返回被移除的键值对
*/
private Data removeItem(){
Data temp = itemDatas[itemNum - 1];
itemDatas[itemNum - 1] = null;
itemNum --;
return temp;
}
}
/**
* 根节点
*/
private Node23 root = new Node23();
……接下来就是一堆方法了
}主要是两个方法:find查找方法和Insert插入方法:看注释
/**
*查找含有key的键值对
* @param key
* @return 返回键值对中的value
*/
public Value find(Key key) {
Node23 curNode = root;
int childNum;
while (true) {
if ((childNum = curNode.findItem(key)) != -1) {
return (Value) curNode.itemDatas[childNum].value;
}
// 假如到了叶子节点还没有找到,则树中不包含key
else if (curNode.isLeaf()) {
return null;
} else {
curNode = getNextChild(curNode,key);
}
}
}
/**
* 在key的条件下获得结点的子节点(可能为左子结点,中间子节点,右子节点)
* @param node
* @param key
* @return 返回子节点,若结点包含key,则返回传参结点
*/
private Node23 getNextChild(Node23 node,Key key){
for (int i = 0; i < node.getItemNum(); i++) {
if (node.getData(i).key.compareTo(key)>0){
return node.getChild(i);
}
else if (node.getData(i).key.compareTo(key) == 0){
return node;
}
}
return node.getChild(node.getItemNum());
}
/**
* 最重要的插入函数
* @param key
* @param value
*/
public void insert(Key key,Value value){
Data data = new Data(key,value);
Node23 curNode = root;
// 一直找到叶节点
while(true){
if (curNode.isLeaf()){
break;
}else{
curNode = getNextChild(curNode,key);
for (int i = 0; i < curNode.getItemNum(); i++) {
// 假如key在node中则进行更新
if (curNode.getData(i).key.compareTo(key) == 0){
curNode.getData(i).value =value;
return;
}
}
}
}
// 若插入key的结点已经满了,即3-结点插入
if (curNode.isFull()){
split(curNode,data);
}
// 2-结点插入
else {
// 直接插入即可
curNode.insertData(data);
}
}
/**
* 这个函数是裂变函数,主要是裂变结点。
* 这个函数有点复杂,我们要把握住原理就好了
* @param node 被裂变的结点
* @param data 要被保存的键值对
*/
private void split(Node23 node, Data data) {
Node23 parent = node.getParent();
// newNode用来保存最大的键值对
Node23 newNode = new Node23();
// newNode2用来保存中间key的键值对
Node23 newNode2 = new Node23();
Data mid;
if (data.key.compareTo(node.getData(0).key)<0){
newNode.insertData(node.removeItem());
mid = node.removeItem();
node.insertData(data);
}else if (data.key.compareTo(node.getData(1).key)<0){
newNode.insertData(node.removeItem());
mid = data;
}else{
mid = node.removeItem();
newNode.insertData(data);
}
if (node == root){
root = newNode2;
}
/**
* 将newNode2和node以及newNode连接起来
* 其中node连接到newNode2的左子树,newNode
* 连接到newNode2的右子树
*/
newNode2.insertData(mid);
newNode2.connectChild(0,node);
newNode2.connectChild(1,newNode);
/**
* 将结点的父节点和newNode2结点连接起来
*/
connectNode(parent,newNode2);
}
/**
* 链接node和parent
* @param parent
* @param node node中只含有一个键值对结点
*/
private void connectNode(Node23 parent, Node23 node) {
Data data = node.getData(0);
if (node == root){
return;
}
// 假如父节点为3-结点
if (parent.isFull()){
// 爷爷结点(爷爷救葫芦娃)
Node23 gParent = parent.getParent();
Node23 newNode = new Node23();
Node23 temp1,temp2;
Data itemData;
if (data.key.compareTo(parent.getData(0).key)<0){
temp1 = parent.disconnectChild(1);
temp2 = parent.disconnectChild(2);
newNode.connectChild(0,temp1);
newNode.connectChild(1,temp2);
newNode.insertData(parent.removeItem());
itemData = parent.removeItem();
parent.insertData(itemData);
parent.connectChild(0,node);
parent.connectChild(1,newNode);
}else if(data.key.compareTo(parent.getData(1).key)<0){
temp1 = parent.disconnectChild(0);
temp2 = parent.disconnectChild(2);
Node23 tempNode = new Node23();
newNode.insertData(parent.removeItem());
newNode.connectChild(0,newNode.disconnectChild(1));
newNode.connectChild(1,temp2);
tempNode.insertData(parent.removeItem());
tempNode.connectChild(0,temp1);
tempNode.connectChild(1,node.disconnectChild(0));
parent.insertData(node.removeItem());
parent.connectChild(0,tempNode);
parent.connectChild(1,newNode);
} else{
itemData = parent.removeItem();
newNode.insertData(parent.removeItem());
newNode.connectChild(0,parent.disconnectChild(0));
newNode.connectChild(1,parent.disconnectChild(1));
parent.disconnectChild(2);
parent.insertData(itemData);
parent.connectChild(0,newNode);
parent.connectChild(1,node);
}
// 进行递归
connectNode(gParent,parent);
}
// 假如父节点为2结点
else{
if (data.key.compareTo(parent.getData(0).key)<0){
Node23 tempNode = parent.disconnectChild(1);
parent.connectChild(0,node.disconnectChild(0));
parent.connectChild(1,node.disconnectChild(1));
parent.connectChild(2,tempNode);
}else{
parent.connectChild(1,node.disconnectChild(0));
parent.connectChild(2,node.disconnectChild(1));
}
parent.insertData(node.getData(0));
}
}
2-3查找树的原理很简单,甚至说代码实现起来难度都不是很大,但是却很繁琐,因为它有很多种情况,而在红黑树中,用巧妙的方法使用了2个结点解决了3个结点的问题。
