补码原理

补码

所有的计算机资料都规定：补码是将各位按位取反，再加1.

学的时候并没有觉得有什么疑问，但是写代码很多年之后，回过头去温习计算机原理，突然冒出来几个问题

为什么要有补码这个东西？为什么补码要按位取反？为什么要有左移右移？

这些都是为了计算机实现加减乘除才出现的。首先讲讲加减，计算机没有减法，所以就是加上负数来替代它。

举个例子吧
2的二进制是0000 0010，那么-2的表示是否是1000 0010呢
验证一下，假如它们成立就必须2+（-2）=0
两者的相加为1000 0100，不管前面符号位是0还是1，这个数都不等于0.

那么我们反过来想，我想要获取一个数的负数是多少，那么只要确保这个数加上它的负数等于0

还是刚刚的例子
2的二进制是0000 0010，那么0的二进制是0000 0000
我们知道二进制加法中，正常情况下2加上任何数都不能等于0，只有一种情况，那就是高位溢出。比如2加上某个数变成了1 0000 0000，这个时候计算机会弃掉高位的1.
这就很简单了，我把2按位取反，变成1111 1101，它加上2就是1111 1111，这个时候我只需要再加1，就能变成1 0000 0000.
所以将2按位取反再加1为 1111 1110，这就是补码。

补码的规则就有了，将各位按位取反，再加1. 补码就是用正数表示的负数形式。

因为符号位的特殊，0000 0000 - 1111 1111 一共能表示256个，所以1个字节表示的无符号范围是0 到2⁸ -1（一共256个），有符号- 2⁷ 到 2⁷-1（一共256个）

好，问题来了，无符号的范围不用说，有符号的范围为什么负数是-128，正数只能到127呢

我们可以看到，有符号位的二进制数第一位是符号，所以剩下的7位表示数
正数范围从0到127没有问题。
1到127对应的数都有其补码，对应了-127到-1
唯独剩下个0，0归为正数，它的二进制是0000 0000，那么现在就剩下一个1000 0000没有表示，因为符号位的原因，它相当于是-0.但是-0也是0，所以规定1000 0000表示负数最大值，也就是128

所以0的补码就是-128，所以有符号位的范围是-128到127

左移和右移

补码的出现是为了表示负数，来做加法和减法。那么左移和右移就是来做乘法以及除法。

左移是指把所有的位向左移动n位数，那么这个数就扩大了2ⁿ倍

左移是指把所有的位向又移动n位数，那么这个数就缩小了2ⁿ倍

这样我们就能实现乘法和除法，比如5*3就变成了5*（2+1）就等于5*2¹+5，也就是将5左移1位，再加上5。

除法假如除数是2的幂次方，比较简单，右移2的幂次位就行，比如5/2，只要把5右移1位得到整数位是2.

那么小数位呢？（小数位比较复杂，这边就不讨论了）假如除数不是2的幂次方呢?

x/y其实就是，x不断减y的过程。小学时候学的长长除法就是这个原理。
用二进制的除法x/y，比十进制容易写，商不是0即是1，而且如果除数大于除数的1倍，商就是标记在另一个位上面了

二进制除法x/y=0.1001/0.1011手工计算如下
           0.11  
     _______
0.1001/0.1001
        10010(后面补0)
        -1011
      ------
        111(余数)
        1110(后面补0)
        -1011
       --------
             1(余数)
           
设ri表示第i次运算后所得的余数,则：
若ri>0，则商1，余数和商左移1位，再减去除数，即ri+1=2ri-y
若ri<0，则商0，余数和商左移1位，再加上除数，即ri+1=2ri+y

用85/6来举例,85/6=1010101/110
a.101(0101)左移1位到第3位都小于110，因此商=000
b.1010(101)左移四位是1010,比110大，商=0001,余数=1010-110=100(101)
c.余数100(101)左移一位是1001,比110大，商=00011,余数=1001-110=11(01)
d.余数11(01)左移一位是110,等于110，商=000111,余数=0(1)
e.余数0(1)左移一位是01,小于110,商=0001110,余数=01

因此85/6=1010101/110=0001110，即14，余数为最后的余数1     

无符号数的左移和右移是没有问题的，往左移相当于增加2倍，往右移是减小2倍，

但是假如是有符号数呢，第一位是符号位，那么直接把后面的7位左移或者右移就可以了吗？

先来看左移

以-2为例
2转换成二进制是0000 0010
2的补码是 1111 1110
对1111 1110左移一位得到1111 1100
将补码-1得到1111 1011，再按位取反得到正数是0000 0100，是4
左移1位相当于是乘以2

所以有符号数的左移也是相当于增加2的幂次方倍

下面看右移，这就涉及到2种方式：

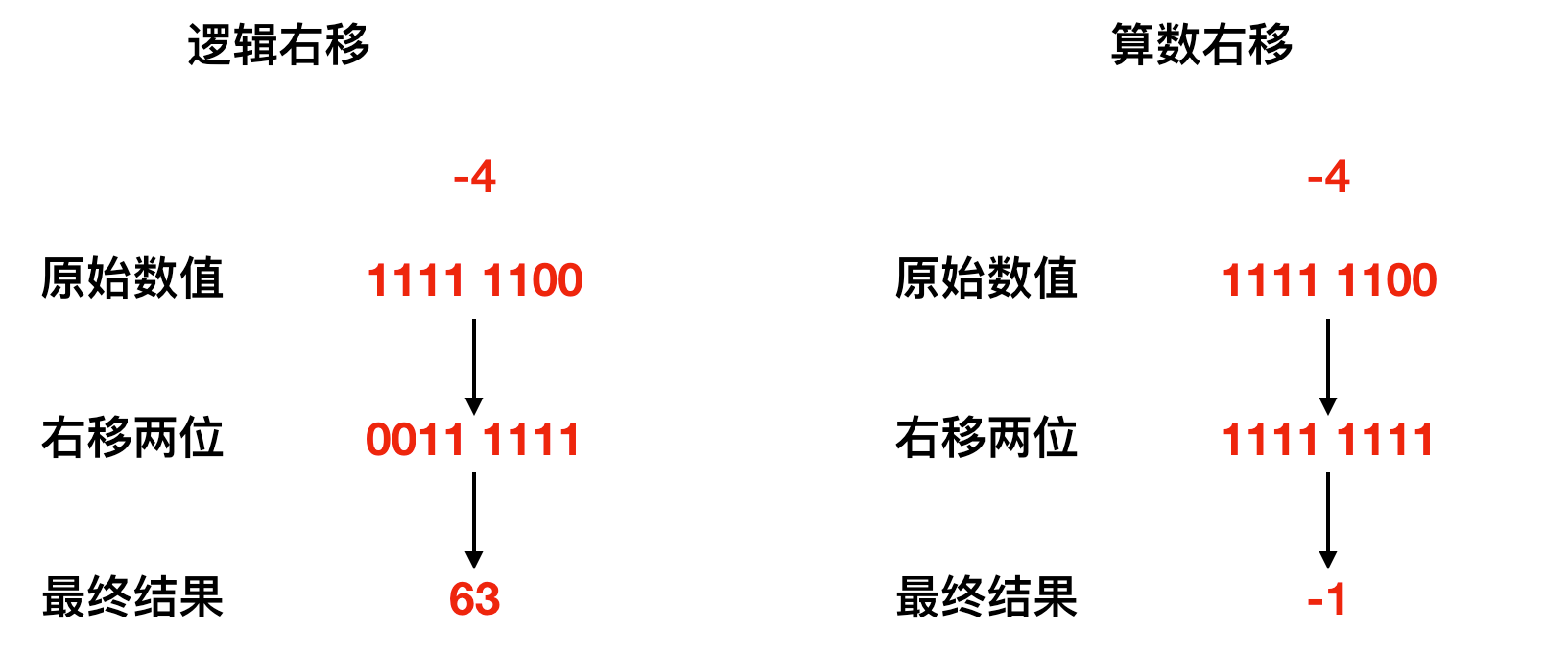
逻辑右移：把所有的位，包括符号位向左或向右移动，高位补0

算术右移：假如是正数，高位补零，假如是负数，高位补1。

看图中的例子，逻辑右移不能得到正确答案，算数右移才是正确的

还是以-4为例子, 我们先看下它的正数的例子
原始数值    0000 0100     
右移两位    0000 0001
最终结果          1

我们还是按结果倒推，-4右移两位我们想要的结果是-1
那么以-1为例，左移两位不就是-4吗
原始数值    1111 1111
左移两位    1111 1100

根据补码的规则，把正数的各位取反加1. 设想一下假如负数右移的过程中把高位取0，那么减去1之后，把各位再取反得到得正数，它得高位将会是1，这显然是不对得。

所以负数得右移应该以算数右移为准。