题目:
给定两个大小为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。
请你找出这两个正序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例 1:
nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0
示例 2:
nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5
思路:
思路:
看示例得知,中位数的概念是奇数情况:为中间位;偶数情况为中间2位之和平均数
python 中的% 和/ 的意思
%取余数
/取整数,
本题的难点是限制时间复杂度为 O(log(m + n))
方法一:
一般解法,先不考虑时间复杂度要求,如果除法运算想保留小数点,被除数保留小数点即可,这样就会有完整结果。
class Solution(object):
def findMedianSortedArrays(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: float
"""
tmp = []
result = 0
for i in nums1:
tmp.append(i)
for n in nums2:
tmp.append(n)
tmp.sort() #排序
p = len(tmp)%2
if p ==0: #偶数
result = (tmp[len(tmp)/2-1]+tmp[len(tmp)/2])*/2.0
else: #奇数
result = tmp[(len(tmp)+1)/2-1]
return result
执行用时 :48 ms, 在所有 Python 提交中击败了76.69%的用户
内存消耗 :12.8 MB, 在所有 Python 提交中击败了11.11%的用户
或者是选用合并再sort,代码更简洁些。
class Solution(object):
def findMedianSortedArrays(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: float
"""
nums = nums1 + nums2
nums.sort()
count = len(nums)
if count % 2 == 0:
return (nums[int(count / 2 - 1)] + nums[int(count / 2)]) / 2.0
else:
return nums[int(count / 2)]
方法二:
想不出来关于时间复杂度的方法实现,这里摘自一个题解大大的思路(作者:louis-38),我觉得很棒,从另一个角度分析了二分法
在统计中,中位数被用来:
将一个集合划分为两个长度相等的子集,其中一个子集中的元素总是大于或等于另一个子集中的元素。
和中位数无关的元素
假设一个集合A被中位数划分成两个长度相等的子集A1和A2,A1中的元素总是小于或等于A2中的元素。
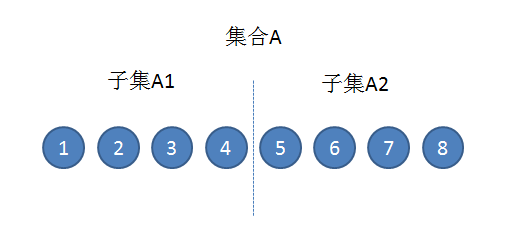
如上图所示的集合A,其中位数是4.5。
当我们同时从A1和A2中移除任意n个元素(不移除A1最大元素和A2最小元素),集合A的中位数是不变的。
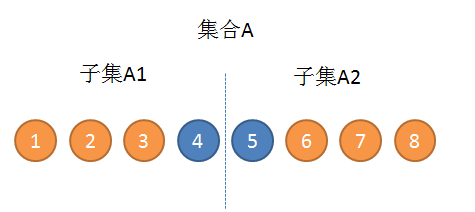
即我们移除A1中的1,2,3这三个元素中的任意n个,同时移除A2中的6,7,8这三个元素的任意n个,集合A的中位数还是4.5。
所以我称1,2,3,6,7,8这几个元素是和中位数无关的元素。即对称地移除他们时,对集合的中位数没有影响。
元素个数为奇数的情况稍有不同,但是也是类似的。
中位数的位置
回到这个题目上。
基于上述的原理,我们是否可以通过排除和中位数无关的元素,最终得到中位数?
此解法的重点是:要知道中位数的位置。(这不是扯淡吗,我知道中位数的位置直接返回不就完了。- -!)
我们这里不是求中位数的确切位置,而是求中位数的大概位置。
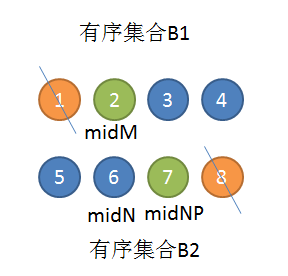
假设题目给出的两个有序集合为B1和B2,他们的长度为m和n。
设 midM = (m-1)/2(暂不考虑m=0的边界情况)
设 midN = (n-1)/2
如果n%2=0:
设midNP = midN + 1
否则midNP = midN
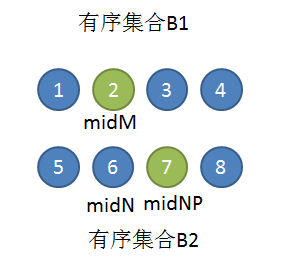
那么这两个集合的并集的中位数的值median,必定是:2<=median<=7。否则median无法将B1和B2的并集切分为等长的两部分。(证明过程就不给出了,数学比较差,但是代码运行结果证明这个推论是正确的。)
所以,根据上述推论可以得出,1,8是和中位数无关的元素。
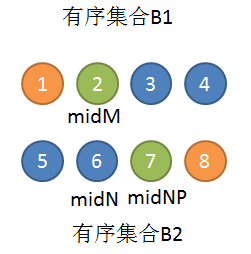
消除元素1和8从而得到更短的两个集合,如下图。其并集中位数不变,还是4.5。
接下来重复以上的步骤。由于每次排除元素的数量是较短集合的一半元素,所以经过log(min(m,n))次迭代之后,到达边界条件。
过程如动图: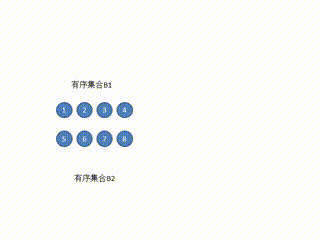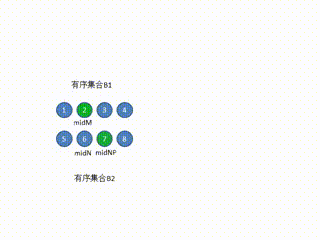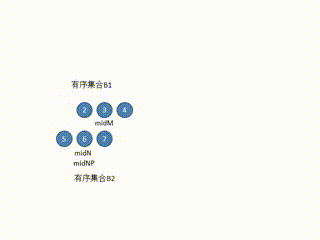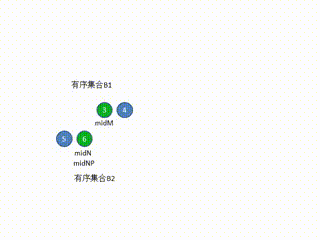
该算法的时间复杂度为O(log(min(m,n)))。
边界条件处理:
最终到达边界的情况下,nums1的长度可能是1或者2。对于这两种情况,我们只需拿nums1剩下的数和nums2中间几位数进行排序,就能得到中位数。
由于进行排序的数组长度最长是6,故其时间复杂度为O(1)。
class Solution(object):
def findMedianSortedArrays(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: float
"""
m = len(nums1)
n = len(nums2)
if n < m:
temp = nums1
nums1 = nums2
nums2 = temp
m = len(nums1)
n = len(nums2)
mid_m = (m - 1) / 2
mid_n = (n - 1) / 2
if m == 0:
return nums2[mid_n] if (n % 2) == 1 else (nums2[mid_n] + nums2[mid_n + 1]) / 2.0
if m == 1 or m == 2:
if n < 3:
nums1.extend(nums2)
elif n % 2 == 1:
nums1.extend(nums2[mid_n - 1:mid_n + 2])
else:
nums1.extend(nums2[mid_n - 1:mid_n + 3])
nums1.sort()
m = len(nums1)
mid_m = (m - 1) / 2
return nums1[mid_m] if m % 2 == 1 else (nums1[mid_m] + nums1[mid_m + 1]) / 2.0
mid_np = mid_n if n % 2 == 1 else mid_n + 1
if nums1[mid_m] == nums2[mid_np]:
return nums1[mid_m]
if nums1[mid_m] < nums2[mid_np]:
return self.findMedianSortedArrays(nums1[mid_m:],nums2[:n-mid_m])
return self.findMedianSortedArrays(nums1[:m-mid_m], nums2[mid_m:])
下面是依据官方题解简化后的代码,比较简洁,但是理解的话需要参考下官方的思路
class Solution(object):
def findMedianSortedArrays(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: float
"""
def getkth(k, l1, l2):
if l1 == m: return nums2[l2 + k - 1]
if l2 == n: return nums1[l1 + k - 1]
if k == 1: return min(nums1[l1], nums2[l2])
# 每次比较从开始起第 k/2-1 个数,并去掉较小的数组的前面部分
new_l1, new_l2 = min(l1 + k / 2, m), min(l2 + k / 2, n)
if nums1[new_l1 - 1] < nums2[new_l2 - 1]:
return getkth(k - new_l1 + l1, new_l1, l2)
else:
return getkth(k - new_l2 + l2, l1, new_l2)
m, n, s = len(nums1), len(nums2), len(nums1) + len(nums2)
if s % 2:
return getkth((s + 1) / 2, 0, 0)
return (getkth(s / 2, 0, 0) + getkth(s / 2 + 1, 0, 0)) / 2.0