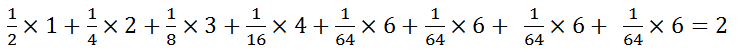最短平均码长（挑出假硬币问题的解法）

学校的计算机系统结构课程讲到了信息源熵，包括自己做习题的时候有求最短平均码长的问题，不是太懂，就在百度搜文章，遇上了这篇贴。而且以前做的算法题有碰到要求至少多少次能挑出假币的问题，由于当时还很年轻，不会二分，做不出来，而且这篇文章刚好讲了另一种用最短平均码长求解的方法，使我恍然大悟。这里先把原文给出来：https://blog.csdn.net/hearthougan/article/details/77774948

如果信息熵不明白的请看这里：https://www.cnblogs.com/xiaoran991/p/12684890.html

首先给出结果：

最短的平均编码长度 = 信源的不确定程度 / 传输的表达能力。

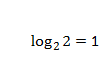
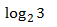
其中信源的不确定程度，用信源的熵来表示，又称之为被表达者，传输的表达能力，称之为表达者表达能力，如果传输时有两种可能，那表达能力就是，如果是传输时有三种可能，那表达能力就是。以例子来描述，尽量做到通俗易懂。

例1：昨天小明错过一场有8匹赛马的比赛，编号为1~8号，每匹马赢的概率都一样，那么作为朋友的你要把获胜马的编号发送给他，那么你该怎么做？

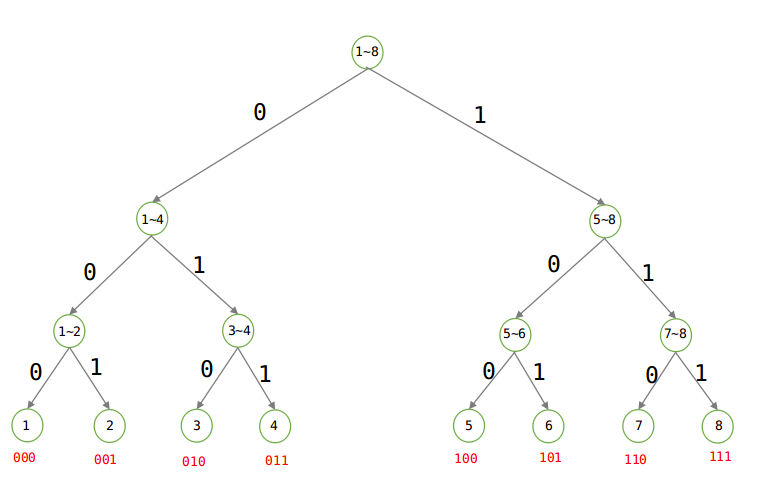
方法一：直接发送马的编号，这样描述一匹马需要3比特（000,001,010,011,100,101,110,111）。

方法二：利用数据结构中的Huffman编码，如下：

建立Huffman树：

由上图可知，当等概率的时候，发送信息仍至少需要3比特。

被表达者：直接根据概率求熵即可，1/8×log8 * 8 = 3比特。

表达者：由图可以看出来Huffman树是一颗二叉树，要么是0，要么是1，所以表达能力就是log2.

平均编码长度 = 3/log2 = 3比特，注意其中的log 都是以2为底的。

例2：昨天小明错过一场有8匹赛马的比赛，编号为1_8号，18号获胜的概率分别为{1/2、1/4、 1/8、 1/16、 1/64、 1/64、 1/64、 1/64}，那么作为朋友的你要把获胜马的编号发送给他，那么你该怎么做？

方法一：仍然直接发送马的编号，这样描述一匹马需要3比特（000,001,010,011,100,101,110,111）。

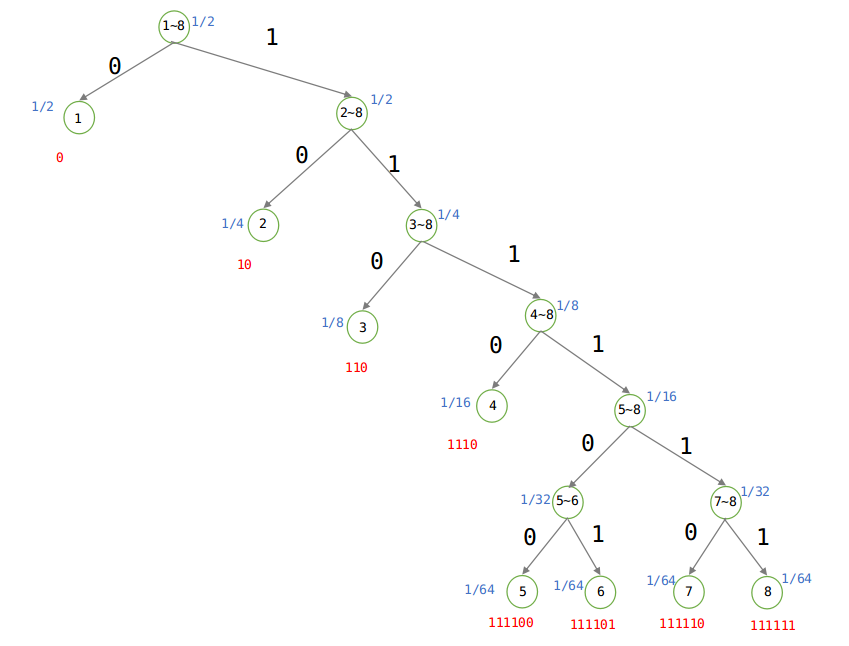
方法二：利用数据结构中的Huffman编码，如下：

建立Huffman树：

由于概率不相等，则根据Huffman树可知平均编码为：（1 × 1/2 + 2 × 1/4 + 3 × 1/8 + 4 × 1/16 + 6 × 1/64 + 6 × 1/64 + 6 × 1/64 + 6 × 1/64） = 2比特，当概率不相等的时候，发送的平均长度为2比特。

由上图可知：

被表达者（不确定程度）：

表达者：由图可以看出来Huffman树是一颗二叉树，要么是0，要么是1，所以表达能力就是log2.

平均编码长度：2/log2 = 2比特。

例3：假设有5个硬币：1,2,3,4,5，其中一个是假的，比其他的硬币轻。有一个天平，天平每次能比较两堆硬币，得出的结果可能是以下三种之一：
左边比右边轻
右边比左边轻
两边同样重
问：至少要使用天平多少次才能保证找到假硬币?

答案：是2次，

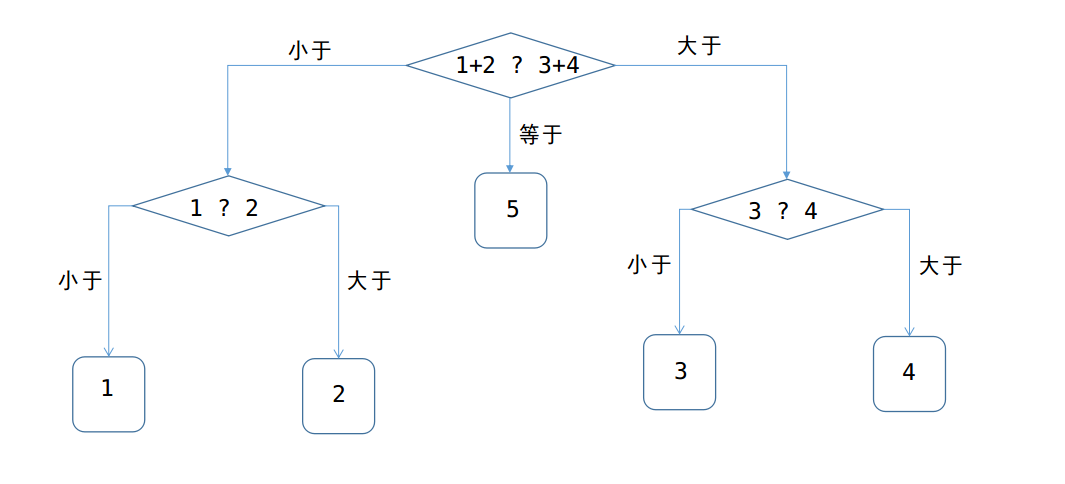
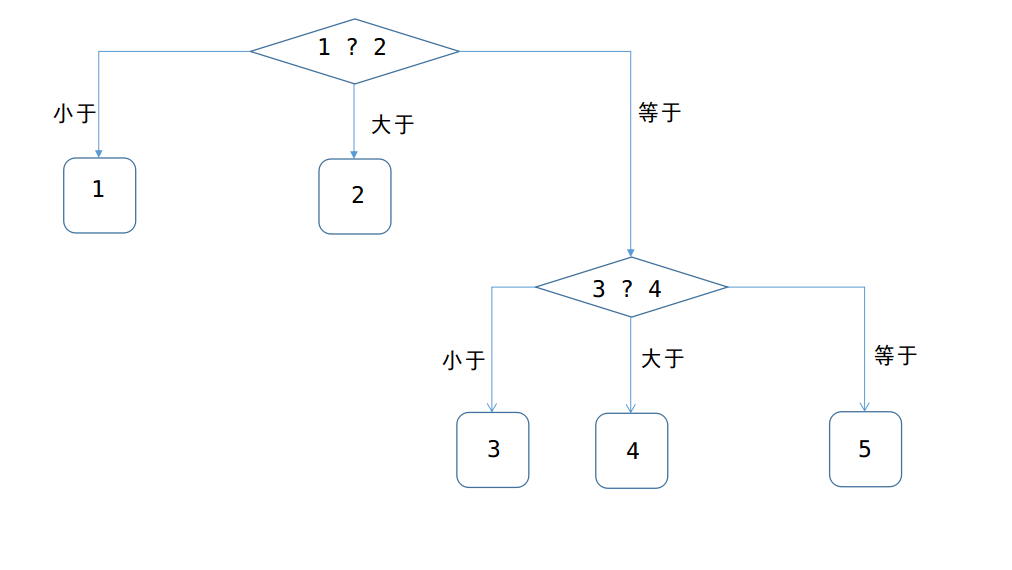
方法一：可作出如下图的抉择：

所以至少称重2次，才可以确保找出。

方法二：

设X表示硬币，Y表示天平，则，X的取值可以是5枚硬币中的任意一枚，每个硬币的概率都是1/5，那么随机变量X的不确定程度就是:

H(X) = 1/5×log5 + 1/5×log5 + 1/5×log5 + 1/5×log5 +1/5×log5 = log5

Y表示天平，A、B两个硬币放在天平，有三种情况：A < B, A > B, A = B。也就是说Y的表达能力就是log3.因此：

平均编码长度: log5 / log3 = 1.46;换算成次数，也就是至少2次可以确保找到假硬币！

例4、假设有5个硬币：1,2,3,…5，其中一个是假的，比其他的硬币轻。已知第一个硬币是假硬币的概率是三分之一；第二个硬币是假硬币的概率也是三分之一，其他硬币是假硬币的概率都是九分之一。
有一个天平，天平每次能比较两堆硬币，得出的结果可能是以下三种之一：
左边比右边轻
右边比左边轻
两边同样重
假设使用天平n次找到假硬币。问n的期望值至少是多少？

方法一：同样利用Huffman编码的思想，得出下图：

 由上图可以知道，至少称重2次才可以找到假硬币，这一题与上一题的差别就是，是每一枚硬币的可能性都不一样，所以先比较概率最大的两枚1,2，找到假币的概率占了2/3，如果不在1 、2中，那么从3~5中随便取出两枚硬币，（上图选取的是3 、4两枚硬币）再称一次，就可以找打假硬币！

方法二：

设X表示硬币，Y表示天平，则，X的取值可以是5枚硬币中的任意一枚，每个硬币的概率分别是{1/3,1/3,1/9,1/9，1/9}，那么随机变量X的不确定程度就是:

H(X) = 1/3 * log3 + 1/3 * log3 + 1/9 *log9 + 1/9 *log9 + 1/9 *log9 = 4/3 *log3;

天平的表达能力同样还是log3；

则平均编码长度：4/3×log 3 / log 3 = 4/3,所以还是需要称重两次。

总结：

由上面4个例子，可以知道很清楚的知道，最短的平均编码长度（也就是我们猜的次数，称重的次数），是由随机变量的熵，除以，表达能力的，得到！