Python基础知识2-内置数据结构(下)

bytes、bytearray

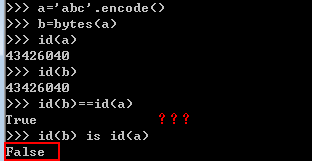
#思考下面例子：
a = 1
b = a
print(a == b)#True
print(a is b)#True
print(id(a) is id(b))#False
print(id(a) == id(b))#True
1. id()：获取的是对象在内存中的地址 
2. is ：比对2个变量的对象引用（对象在内存中的地址，即id() 获得的值）是否相同。如果相同则返回True，否则返回False。换句话说，就是比对2个变量的对象引用是否指向同一个对象。 
3. ==：比对2个变量指向的对象的内容是否相同。
参考：https://segmentfault.com/q/1010000015117621

#用id(expression a) == id(expression b)来判断两个表达式的结果是不是同一个对象的想法是有问题的
#只有你能保证对象不会被销毁的前提下，你才能用 id 来比较两个对象
print(id(a.__init__) == id(a.zhuangshi))#True
z  =a.__init__
x = a.zhuangshi
print(id(z) == id(x))#False
print(id(1)is id(1))#False
print(id(1) == id(1))#False
参考：https://www.jianshu.com/p/Rvkrdb

 bytes定义

bytes操作

bytearray定义

 

bytearray操作

 

线性结构

切片

 练习：

#要求m行k个元素
#思路1：m行有m个元素，k不能大于m，这个需求需要保存m行的数据，那么可以使用一个嵌套机构[[],[],[]]
triangle=[]
m=5
k=4
for i in range(m):#0~4#杨辉三角每行都是以1开头
    row=[1]
    triangle.append(row)
    if i==0:
        continue
    for j in range(1,i):
        row.append(triangle[i-1][j-1]+triangle[i-1][j])
    row.append(1)
print(triangle)
print(triangle[m-1][k-1])

#上例测试效率：

#思路2：根据杨辉三角的定理：第m行的第k个数可表示为C（m-1，k-1），即为从m-1个不同的元素中取k-1个元素的组合数。

#利用c(n,r)=n!/(r!(n-r)!)
m=9
k=5
n = m-1
r = k-1
d = n-r
targets = [] #r,n-r,n
factorial=1
for i in range(1,n+1):
　　factorial *=i
　　if i==r:
　　　　targets.append(factorial)
　　if i==d:
　　　　targets.append(factorial)
　　if i==n:
　　　　targets.append(factorial)
print(targets[2]//(targets[0]*targets[1])) 

#上例测试效率：

练习2

 

#方法1，常规写法
matrix = [[1,2,3],[4,5,6],[7,8,9]]
count = 0 
for i in  range(len(matrix)):
　　for j in range(i):#j<i
　　　　matrix[i][j]=matrix[j][i]
　　　　count+=1
print(matrix)
#方法2：利用enumerate函数创建索引
matrix = [[1,2,3],[4,5,6],[7,8,9]]
count = 0
for i,row in enumerate(matrix):
　　for j in enumerate(row):
　　　　if i<j:
　　　　　　matrix[i][j]=matrix[j][i]
　　　　　　count+=1
print(matrix)

练习3

#思路1：首先新建一个空的列表tm，扫描matrix第一行，在tm的第一列从上至下附加，然后在第二列附加，以此列推。
matrix = [[1,2],[3,4],[5,6]]
tm=[]
for row in matrix:
    for index,col in enumerate(row):
        if len(tm)<index+1:#matrix有index列就要为tm创建index行
            tm.append([])

        tm[index].append(col)
print(tm)
#思路2：考虑能否一次性开辟好空间目标矩阵的内存空间？如果能够一次性开辟好空间目标矩阵内存空间，那么原矩阵的元素直接移动到转置矩阵的对称坐标就行了
#在原有矩阵上改动，牵扯到增加元素和减少元素，有些麻烦，所以，定义一个新的矩阵输出
matrix = [[1,2,3],[4,5,6]]
tm=[[0 for col in range(len(matrix))]for row in range(len(matrix[0]))]
count=0
for i,row in enumerate(tm):
    for j,col in enumerate(row):
        tm[i][j]=tm[j][i]
        count+=1
print(matrix)
print(tm)
print(count)　

#考虑上面两种方法的时间效率比较：(对于大矩阵运算，方法二效率更高一些)　
#测试发现，其实只要增加到4*4的矩阵，方法二的优势就开始了。
#矩阵规模越大，先开辟空间比后append的效率高！　

练习4 

#思路：利用类似linux中位图的思想来记录当前标记数字是否重复出现

import random

nums=[]
for _ in range(10):
    nums.append(random.randrange(1,21))

length=len(nums)
samenums=[]    #记录相同的数字
diffnums=[]    #记录不同的数字
states=[0]*length   #记录不同的索引异同状态

for i in range(length):
    flag = False  #该状态表示没有重复
    if states[i]==1:
        continue
    for j in range(i+1,length):#对每一个数将其与之前的数进行比较
        if states[j]==1:
            continue
        if nums[i]==nums[j]:
            flag=True
            states[j]=1
    if flag:
        samenums.append(nums[i])
        states[i]=1
    else:
        diffnums.append(nums[i])
print(samenums)
print(diffnums)

IPython的使用

帮助

 shell命令

特殊变量

魔术方法

封装和解构

解构(unpack)

Python3的解构

 

丢弃变量

lst=list(range(10))
_,sec,_four,*_,2tail,_=lst

#题目1
_,(*_,a),_=lst
#题目2
s="JAVA_HOME=/usr/bin"
name,_,path=s.partition('=')
#题目3
lst = [1,9,8,5,6,7,4,3,2]
for i in range(len(lst)):
　　flag = False
　　for j in range(len(lst)-i-1):
　　　　if(lst[j+1]<lst[j]):
　　　　　　lst[j+1],lst[j]=lst[j],lst[j+1]
　　　　　　flag = True
　　if not flag:
　　　　break
　　
小结：
　　解构，是Python提供的很好的功能，可以方便的提取复杂数据结构的值。
　　配合_的使用，会更加顺利。 

集set

 

set定义初始化

 

初始化set的时候，里面的元素不能是可变类型，如list，bytearray等

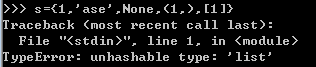
set的元素

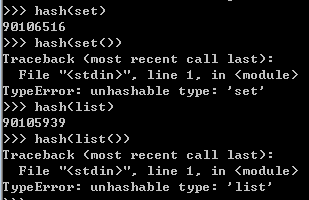
 set增加

set删除

注意这里的remove是根据hash值来找到元素并移除的！所以时间复杂度是O(1).

set修改、查询

这个效率相当于用索引访问顺序结构！时间复杂度为O(1)。

set成员运算符的比较

 

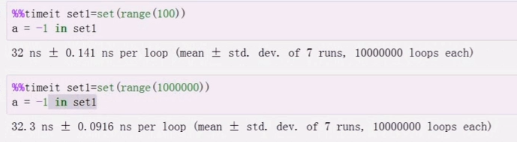
可以看出set集合查询效率跟数据规模无关！ 

set和线性结构

 集合

 集合运算

 

 

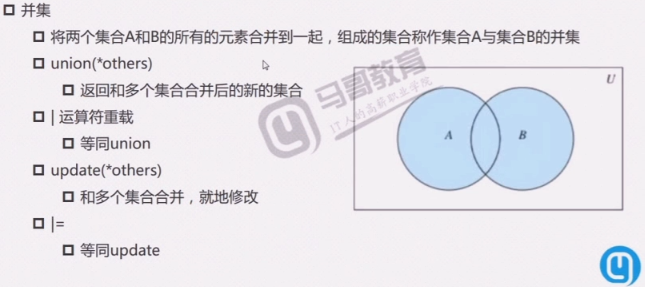
解题思路：

  

集合练习

#利用集合来解决

简单选择排序

 简单选择排序代码实现(一)

 

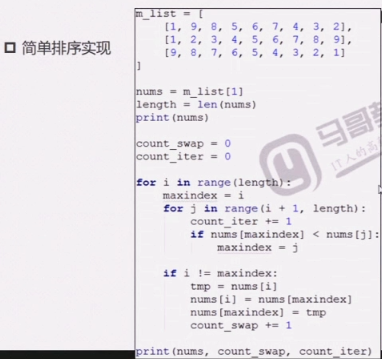
简单选择排序代码实现(二)

 

#二元选择排序（降序）
# lst = [9,2,1,4,5,7,6,8,3]
lst=[1,1,1,1,1,1,1]
print("原序列:",lst)
length = len(lst)
count_swap = 0
count_iter = 0

for i in range(length//2):
    maxindex = i
    minindex = -i-1
    # minorginindex = minindex
    for j in range(i+1,length-i):#!!!
        count_iter += 1
        if lst[maxindex]<lst[j]:
            maxindex = j
            count_swap += 1
        if lst[minindex]>lst[-j-1]:
            minindex = -j-1
            count_swap += 1

    if lst[minindex] == lst[maxindex]:#元素相同说明已经有序
        break

    if i != maxindex:
        lst[maxindex],lst[i] = lst[i],lst[maxindex]
        #如果minindex的索引被交换过(即刚好最大值的索引和最小值的索引交换过)，则需要更新！
        if i == minindex+length:
            minindex = maxindex

    if (-i-1) != minindex or (-i-1+length) != minindex:
        lst[minindex], lst[-i-1] = lst[-i-1], lst[minindex]
print("排序后：",lst)
print("比较次数：{0} 交换次数：{1}".format(count_iter,count_swap))

使用二元排序的时候需要注意几点：
1.相比于(一元)简单选择排序，我们需要再添加一个变量来记录极值的下标。
2.如果两个极值的下标索引只要有一个被交换过则我们需要注意更新另一个极值的下标索引。
3.如果使用了负索引来记录下标，则在比较判断时我们需要注意索引不能为负。

 简单选择排序总结

字典dict

字典dict定义初始化

 

#上述红色标记才是最为常用的初始化格式

 字典元素的访问

 字典的增加和修改

 

字典删除

字典遍历

Python中有序字典OrderedDict (参考：https://www.cnblogs.com/tianyiliang/p/8260741.html)

字典练习

waitting...

标准库datetime

   

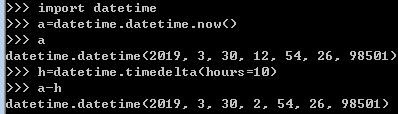
注意：total_seconds()是属于timedelta对象的方法！

 标准库time

 

 Python解析式、生成器

列表解析

注意一下下列情况：

 

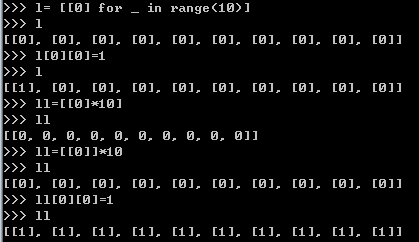
列表解析进阶

 

输出都是[(5,24),(6,24)]

列表解析练习

1.　　[x**2 for x in range(1,11)]
2.　　lst=[1,4,9,16,2,5,10,15]
　　　[lst[i]+lst[i+1] for i in range(len(lst)-1)]
3.　 [print("{}*{}={:<3}{}".format(j,i,i*j,'
' if i==j else ''),end='' )for i in range(1,10) for j in range(1,i+1)]
4 　　["{:>04}.{}".format(i,''.join([chr(random.randint(97,123))for _ in range(10)]))for i in range(1,101)]　　

生成器表达式 

结果会报异常：first和second都为None！

 集合解析式

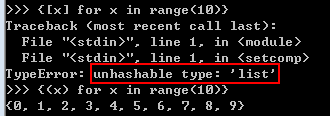
字典解析式

 

总结 

 

 内建函数

 

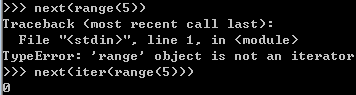
 可迭代对象

 

 迭代器

迭代器不一定是生成器，但生成器本质是迭代器！

字典练习

#按统计次数降序输出
import random
random_alphatable = [''.join([chr(random.randint(97,122))for _ in range(2)])for _ in range(1,101)]
dict_count={}
for i in random_alphatable:
    if i not in dict_count:
        dict_count[i] = 1
    else:
        dict_count[i] += 1
#即按字典的value排序
res = sorted(dict_count.items(),key=lambda items:items[1],reverse=True)
print(type(res))
for i in res:
    print(i,end=" ")