Python进阶2---树的遍历和堆排序

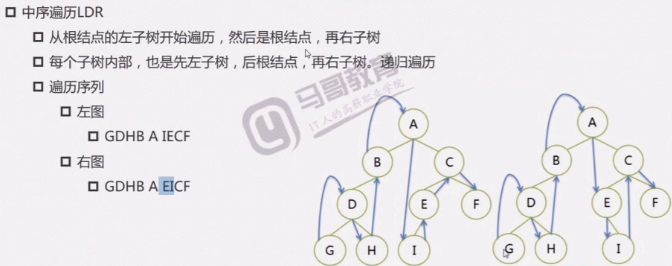
二叉树的遍历

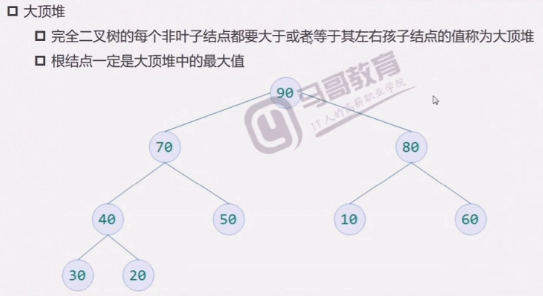
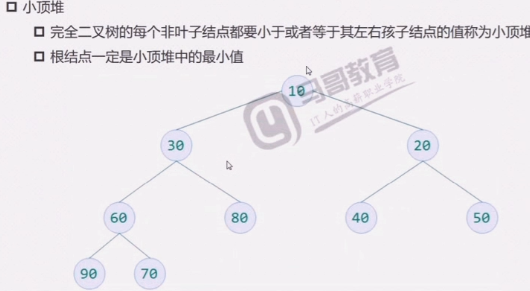
堆排序Heap Sort

 

堆排序的过程

 

 

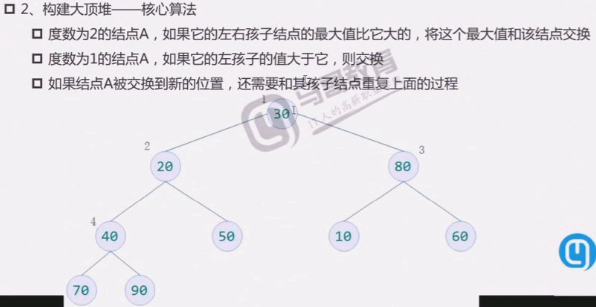
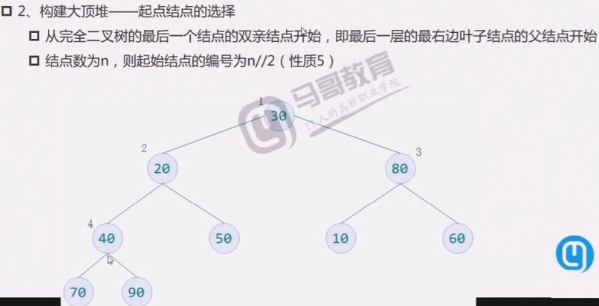
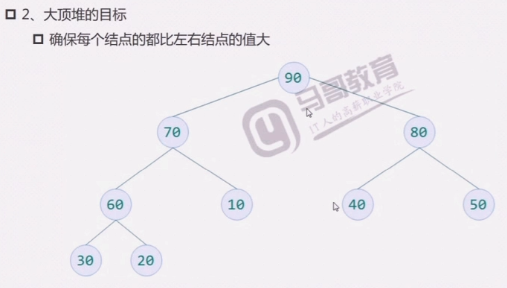
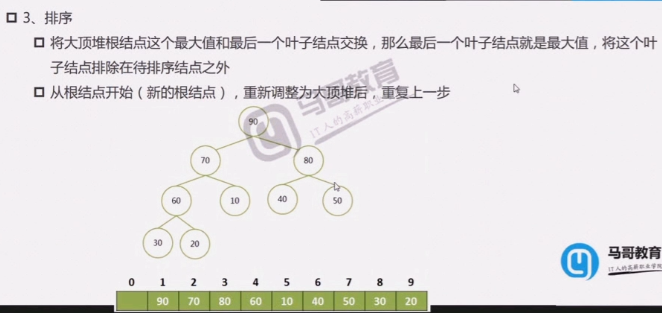
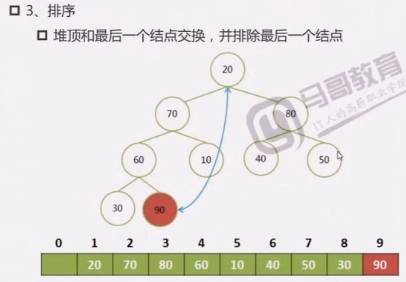
完整过程：

#打印完整的二叉树
import math
#打印完全二叉树，此函数非必要只是为了显示便利！
def print_tree(lst):
    length = len(lst)-1
    depth = int(math.log2(length))+1
    # print('length,depth:',length,depth)
    width = pow(2,depth)-1
    index= 1

    for i in range(depth):
        for j in range(2**i):
            print('{:^{}}'.format(lst[index],width),end=' ')
            index += 1
            if index>length:
                break
        print()
        width = width//2


#堆排序过程如下：
# lst = [0]+[x for x in range(1, 9)]
origin = [0,30,20,80,40,50,10,60,70,90]
total = len(origin)-1
print_tree(origin)
print('='*50)

#核心代码：单次交换最大结点
def heap_adjust(n,i,array:list):
    '''n代表结点个数，i代表从第i结点开始向下遍历'''
    while 2*i<=n:
        leftindex = 2*i
        maxindex = leftindex
        # print(maxindex,leftindex)#4,8
        if n > leftindex and array[leftindex+1] > array[leftindex]:#说明还有右孩子
            maxindex = leftindex+1

        if array[maxindex]>array[i]:
            array[i], array[maxindex] = array[maxindex], array[i]
            i = maxindex  # 因为每次交换后可能会影响子结点的大根堆情况！所以还需要判断子结点
        else:
            break


#构建大顶堆
def create_maxheap(n,array:list):#传的是引用所以可以不需要返回值
    i = n//2
    while i>0:
        heap_adjust(n,i,array)
        i -= 1
    return array

print(create_maxheap(total,origin))
print_tree(origin)
print('-'*50)


#排序：
def sort_heap(total,array:list):

    while total>1:

        array[total],array[1] = array[1],array[total]
        total -= 1
        #优化
        # if total ==2 and array[total]>=array[total-1]:
        #     break
        heap_adjust(total,1,array)

    return array

print_tree(sort_heap(total,origin))
print_tree(origin)