loss与准确率的关系
目录
目录
在进行一项分类任务训练时,观察到验证集上的accuracy增加的同时,loss也在增加,因此产生了一些疑惑,对accuracy和loss之间的关系进行探索。

定义
在理解他们的关系之前,先来回顾一下什么是交叉熵损失和准确率。交叉熵损失函数:交叉熵输出的是正确标签的似然对数,和准确率有一定的关系,但是取值范围更大。交叉熵损失公式:
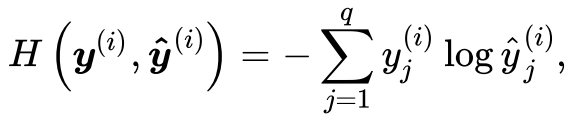
其中y ^ ( i ) widehat{y}^{(i)}y(i)为预测值,y ( i ) y^{(i)}y(i)为真实标签,可以看出交叉熵损失只关心对正确类别的预测概率。(在这里为简化讨论,我们假设一个样本里只要一个标签,即简单的0-1二分类问题。)
当训练样本为n时,交叉熵损失函数为:
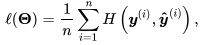
准确率:在分类问题中,准确率的定义简单粗暴,就是看预测的类别是否和真实的类别一致。在分类任务中,对于一个N类任务,输出就是一个N维的向量,向量每一个位置就代表了一种类别,对应位置的值就代表预测的目标属于该类的概率,比如猫狗的分类,输出向量为[0.3, 0.7],就表示输入的图属于猫的概率为0.3,属于狗的为0.7。在输出预测结果时,我们是取概率最大的索引所对应的的标签作为最终预测的结果标签,比如在上个例子中,预测输出:输入的图像类别为狗。
关系
清楚了定义之后,仔细思考就会发现其中的问题,因为准确率是输出最大的概率,因此0.9的概率值和0.5的概率值效果是等价的,只要保证他们是最大概率即可!请看下面的例子:
比如我们现在预测猫和狗的类别,
有一个样本预测输出是[0.1, 0.9], 它的交叉熵损失为loss = -1* log(0.9) = 0.046, 预测结果为:狗
另一个样本的预测输出是[0.4, 0.6], 它的交叉熵损失为loss = -1 * log(0.6) = 0.222, 预测结果为:狗
可以看出两个样本都预测的为狗,但是他们的交叉熵损失差别很大。因此我们在训练时,可能会出现准确率和交叉熵同时上升的情况。
那么问题来了:
既然准确率和损失都是评价模型好坏的,那么用一个不行吗?为什么要用两个并不完全等价的评价指标呢?
这是因为,在分类问题中,可能准确率更加的直观,也更具有可解释性,更重要,但是它不可微,无法直接用于网络训练,因为反向传播算法要求损失函数是可微的。而损失函数一个很好的性质就是可微,可以求梯度,运用反向传播更新参数。即首选损失不能直接优化(比如准确率)时,可以使用与真实度量类似的损失函数。 损失函数的可微性,使得可以采用多种方式进行优化求解,例如牛顿法、梯度下降法、极大似然估计等。另外在分类任务中,使用accuracy可以,但是在回归任务中,accuracy便不再可用,只能使用loss。
- 通过模型在 dev/test 集上的 accuracy ,计算模型正确分类的样本数与总样本数之比以衡量模型的效果,目标是对模型的效果进行度量。
- 通过损失函数的计算,更新模型参数,目标是为了减小优化误差(Optimization error),即在损失函数与优化算法的共同作用下,减小模型的经验风险。
总结准确度和交叉熵会出现以下情况:
- 如果正确标签的概率降低,但这个标签依然是概率最高的,会出现损失增加单准确度不变的结果。
- 如果数据集的标签很不平均,比如90%是类别A,那么模型一味增加预测A的比例,可能会让准确度上升,但loss可能也会以更大幅度上升(cross entropy的幅度可以很大)
- 如果模型非常自信,大多数正确标签的概率都接近1,那如果出现一个错误,准确率可能只会降低很少,但交叉熵可能会非常高。
参考:
https://blog.csdn.net/quiet_girl/article/details/86138489
https://www.zhihu.com/question/264892967