算法与数据结构——排序（十二）计数排序

      计数排序是一种理解起来非常容易的排序算法，以前我们学习到的排序算法都是比较排序，而它不是一种比较排序算法，它的时间复杂度是O(n)，它的原理其实很简单，我们在基数排序里面就已经用到了。

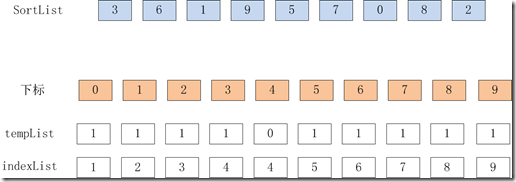
      它首先用一个数组tempList，记录待排序列sortList中每个数出现的次数。tempList[i]代表是的待排序列中i出现的次数，tempList[5]=2，代表待排序列中5出现了两次。

      然后用一个数组indexList记录比当前数小的所有数小的个数。indexList[i]代表的是待排序列中比i小的数出现的个数，indexList[3]=2，代表待排序列中比3小的数总共有2个，indexList[3]=tempList[0]+tempList[1]+tempList[2].

      indexList计算出来了，那么其实就已经知道了这个数的位置了，indexList[3]=2，代表待排序列中比3小的数字有2个，那么证明3在排序好的数组里面的位置应该是位置3了，依次读出所有的indexList的值，然后按照这些值把数字放入到相应的位置就行了。示意图如下：

代码如下（代码的实现可能与上面的分析有一些不一样，但原理是一样）：

public void CSort(List<int> sortList,int max)
{
    int[] tempList = new int[max+1];//桶的个数比待排序列中最大数的值还要多一个
    int[] tempResult = new int[sortList.Count];//最后存放结果的数组

    //tempList[k]记录的是待排数组中，值为k的数的个数
    for (int j = 0; j < sortList.Count; j++)
    {
        tempList[sortList[j]] += 1;
    }

    for (int j = 0; j < sortList.Count; j++)
    {
        int m = sortList[j];
        int sumCount = 0;
        for (int k = 0; k < m; k++)
        {
            sumCount += tempList[k];
        }
        while (tempResult[sumCount] != 0)
        {
            sumCount++;
        }
        tempResult[sumCount] = sortList[j];
    }

    for (int m = 0; m < sortList.Count; m++)
    {
        sortList[m] = tempResult[m];
    }
}

从代码中我们可以看出，待排序列中的数越大，需要的桶（对应于额外的空间）就越多，所以计数排序，只适合在待排序列中数比较小的情况下使用。对比较小的数进行排序，计数排序是最快的。