收集树上所有苹果的最少时间
题目
给你一棵有 n 个节点的无向树,节点编号为 0 到 n-1 ,它们中有一些节点有苹果。通过树上的一条边,需要花费 1 秒钟。你从 节点 0 出发,请你返回最少需要多少秒,可以收集到所有苹果,并回到节点 0 。
无向树的边由 edges 给出,其中 edges[i] = [fromi, toi] ,表示有一条边连接 from 和 toi 。除此以外,还有一个布尔数组 hasApple ,其中 hasApple[i] = true 代表节点 i 有一个苹果,否则,节点 i 没有苹果。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/minimum-time-to-collect-all-apples-in-a-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
根据题目信息建立邻接表,基于后序遍历(自身节点最后处理)的信息传递。
采用DFS,对于与当前节点邻接的邻接点有以下情况
- 叶子点,仅有一条路径,这条路径是通往当前节点的。
- 非叶子点,有两条路径以上(包括两条)
对于当前节点的子路径,最少时间计算有以下情况。
子路径中直接与当前节点邻接的点记为连接点。
- 子路径是叶子点:
- 如果有苹果,通过 时间+2。
- 子路径非叶子点:
- 设tmp为收集子子路径们所有苹果的最少时间,时间 + temp + 2(要通过连接点)
- 子路径不是叶子点,且 子子路径们(当前节点的子路径的所有的子路径)都没有苹果。
- 如果连接点有苹果,通过 时间 + 2
前方高能,灵魂画手。
叶子点、非叶子点和子路径不存在:
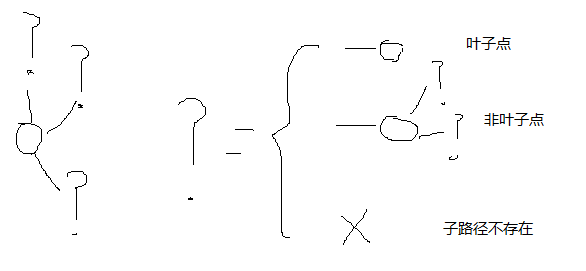
3中计算时间的情况:
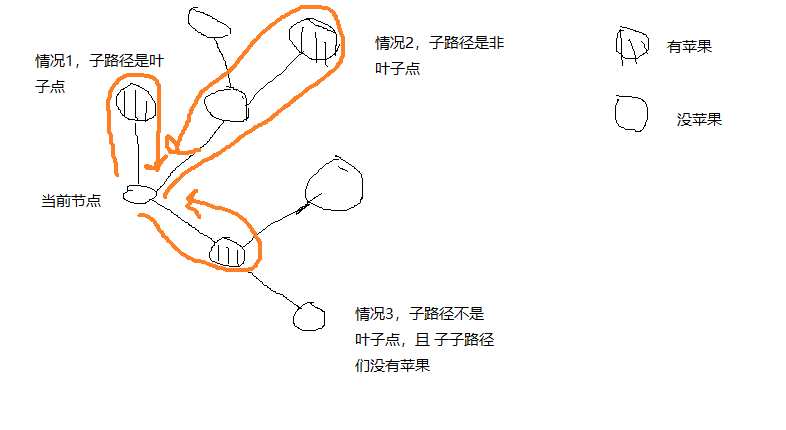
代码
var minTime = function (n, edges, hasApple) {
const map = {};
edges.map((value, index) => {
if (map[value[0]]) map[value[0]].push(value[1]);
else map[value[0]] = [value[1]];
if (map[value[1]]) map[value[1]].push(value[0]);
else map[value[1]] = [value[0]];
});
const dfs = (rec, par, chi, b) => {
// 处理叶子点,这里返回-2是与非叶子进行区分。
if (rec[chi].length == 1 && rec[chi][0] == par && b[chi]) return -2;
if (rec[chi].length == 1 && rec[chi][0] == par && !b[chi]) return 0;
let ans = 0;
for (let i = 0; i < rec[chi].length; ++i) {
// 避免 图:往回走,树:往上走
if (rec[chi][i] != par) {
let tmp = dfs(rec, chi, rec[chi][i], b);
// 处理三种情况,叶子点(连接点)上有苹果
if (tmp < 0) ans += 2;
// 子路径上有苹果,不管连接上有没有苹果都要经过连接点
else if (tmp > 0) ans += tmp + 2;
// 所有子路径上没有苹果(只有连接点有苹果不算),但连接点上有苹果。
else if (b[rec[chi][i]]) ans += 2;
}
}
return ans;
};
return dfs(map, -1, 0, hasApple);
};
说明
判断叶子点:
邻接表长度为1,且仅有的一个邻接点为上次的入口点。
rec[chi].length == 1&& rec[chi][0] == par;
避免从子路径进入当前临界点的子路径(往回走)。
rec[chi][i] != par
参考:
这种题目很多都是基于后续遍历的信息传递
dfs返回的是此子树摘苹果需要的路径ans
如果一个点的子节点ans大于0,则说明摘时必经此子树,因此本节点ans需要+2
如果一个点的子节点ans等于0,并且此节点为false,则说明摘时不必经过此子树
如果一个点的子节点ans等于0,并且此节点为true,则说明摘时需要经过此子节点,本节点ans需要+2
综上所示可以写出下面的代码。
作者:bubbly-4
链接:https://leetcode-cn.com/problems/minimum-time-to-collect-all-apples-in-a-tree/solution/jian-jian-dan-dan-20xing-dai-ma-ji-yu-hou-xu-bian-/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。