ISOMAP

zoukankan html css js c++ java

ISOMAP
转载 https://blog.csdn.net/dark_scope/article/details/53229427#

维度打击，机器学习中的降维算法：ISOMAP & MDS

降维是机器学习中很有意思的一部分，很多时候它是无监督的，能够更好地刻画数据，对模型效果提升也有帮助，同时在数据可视化中也有着举足轻重的作用。

一说到降维，大家第一反应总是PCA，基本上每一本讲机器学习的书都会提到PCA，而除此之外其实还有很多很有意思的降维算法，其中就包括isomap，以及isomap中用到的MDS。

ISOMAP是‘流形学习’中的一个经典算法，流形学习贡献了很多降维算法，其中一些与很多机器学习算法也有结合，但上学的时候还看了蛮多的机器学习的书，从来没听说过流形学习的概念，还是在最新的周志华版的《机器学习》里才看到,很有意思，记录分享一下。

流形学习

流形学习应该算是个大课题了，它的基本思想就是在高维空间中发现低维结构。比如这个图：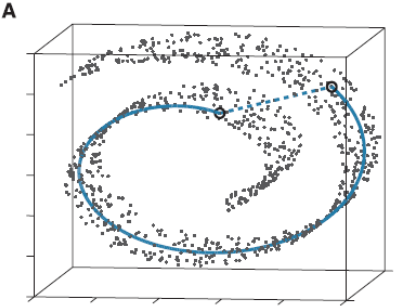
这些点都处于一个三维空间里，但我们人一看就知道它像一块卷起来的布，图中圈出来的两个点更合理的距离是A中蓝色实线标注的距离，而不是两个点之间的欧式距离（A中蓝色虚线）。

此时如果你要用PCA降维的话，它根本无法发现这样卷曲的结构（因为PCA是典型的线性降维，而图示的结构显然是非线性的），最后的降维结果就会一团乱麻，没法很好的反映点之间的关系。而流形学习在这样的场景就会有很好的效果。

我对流形学习本身也不太熟悉，还是直接说算法吧。

ISOMAP

在降维算法中，一种方式是提供点的坐标进行降维，如PCA；另一种方式是提供点之间的距离矩阵，ISOMAP中用到的MDS(Multidimensional Scaling)就是这样。
在计算距离的时候，最简单的方式自然是计算坐标之间的欧氏距离，但ISOMAP对此进行了改进，就像上面图示一样：

1.通过kNN(k-Nearest Neighbor)找到点的k个最近邻，将它们连接起来构造一张图。
2.通过计算同中各点之间的最短路径，作为点之间的距离 $d_{i j}$

ISOMAP本身的核心就在构造点之间的距离，初看时不由得为其拍案叫绝，类似的思想在很多降维算法中都能看到，比如能将超高维数据进行降维可视化的t-SNE。
ISOMAP效果，可以看到选取的最短路径比较好地还原了期望的蓝色实线，用这个数据进行降维会使流形得以保持：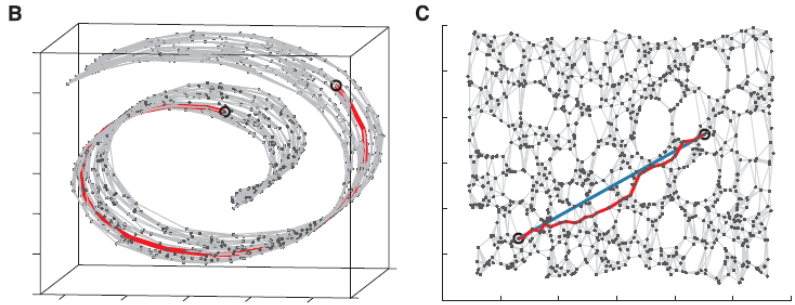

ISOMAP算法步骤可谓清晰明了，所以本文主要着重讲它中间用到的MDS算法，也是很有意思的。

经典MDS（Multidimensional Scaling）

如上文所述，MDS接收的输入是一个距离矩阵 $D$

所以想要从 $D$

我们不妨假设： $X$

$\begin{aligned} B & = X X^{T} (n \times n) \\ = (X M) (X M)^{T} (M 是一组正交基) \\ = X M M^{T} X \\ = X X^{T} \end{aligned}$

可以看到我们通过 $M$

B中每个元素的值为：

$\begin{aligned} b_{i j} & = \sum_{k = 1}^{q} x_{i k} x_{j k} \end{aligned}$

$M$

$\begin{aligned} d_{i j}^{2} & = (x_{i} - x_{j})^{2} \\ = \sum_{k = 1}^{q} (x_{i k} - x_{j k})^{2} \\ = \sum_{k = 1}^{q} x_{i k}^{2} + x_{j k}^{2} - 2 x_{i k} x_{j k} \\ = b_{i i} + b_{j j} - 2 b_{i j} \end{aligned}$

$M$

所以思路是：从D->B->X
此时我们要对X加一些限制，前面说过我们平移所有点是不会对距离矩阵造成影响的，所以我们就把数据的中心点平移到原点，对X做如下限制（去中心化）：

$\begin{aligned} \sum_{i = 1}^{n} x_{i k} = 0, f o r a l l k = 1.. q \end{aligned}$

$M$

$\begin{aligned} \sum_{j = 1}^{n} b_{i j} & = \sum_{j = 1}^{n} \sum_{k = 1}^{q} x_{i k} x_{j k} \\ = \sum_{k = 1}^{q} x_{i k} (\sum_{j = 1}^{n} x_{j k}) \\ = 0 \end{aligned}$

$M$

$\begin{aligned} \sum_{i = 1}^{n} b_{i j} & = \sum_{i = 1}^{n} \sum_{k = 1}^{q} x_{i k} x_{j k} \\ = \sum_{k = 1}^{q} x_{j k} (\sum_{i = 1}^{n} x_{i k}) \\ = 0 \end{aligned}$

$M$

设T为 $B$

$\begin{aligned} \sum_{i = 1}^{n} d_{i j}^{2} & = \sum_{i = 1}^{n} b_{i i} + b_{j j} - 2 b_{i j} \\ = T + n b_{j j} + 0 \end{aligned}$

$M$

$\begin{aligned} \sum_{j = 1}^{n} d_{i j}^{2} & = \sum_{j = 1}^{n} b_{i i} + b_{j j} - 2 b_{i j} \\ = n b_{i i} + T + 0 \end{aligned}$

$M$

$\begin{aligned} \sum_{i = 1}^{n} \sum_{j = 1}^{n} d_{i j}^{2} & = 2 n T \end{aligned}$

$M$

$\begin{aligned} b_{i j} & = - \frac{1}{2} (d_{i j}^{2} - b_{i i} - b_{j j}) \end{aligned}$

$M$

$\begin{aligned} b_{i i} & = \frac{T}{n} + \frac{1}{n} \sum_{j = 1}^{n} d_{i j}^{2} \\ b_{j j} & = \frac{T}{n} + \frac{1}{n} \sum_{i = 1}^{n} d_{i j}^{2} \\ \frac{2 T}{n} & = \frac{1}{n^{2}} \sum_{i = 1}^{n} \sum_{j = 1}^{n} d_{i j}^{2} \end{aligned}$

$M$

$\begin{aligned} b_{i j} & = - \frac{1}{2} (d_{i j}^{2} - b_{i i} - b_{j j}) \\ = - \frac{1}{2} (d_{i j}^{2} - \frac{1}{n} \sum_{j = 1}^{n} d_{i j}^{2} - \frac{1}{n} \sum_{i = 1}^{n} d_{i j}^{2} + \frac{2 T}{n}) \\ = - \frac{1}{2} (d_{i j}^{2} - \frac{1}{n} \sum_{j = 1}^{n} d_{i j}^{2} - \frac{1}{n} \sum_{i = 1}^{n} d_{i j}^{2} + \frac{1}{n^{2}} \sum_{i = 1}^{n} \sum_{j = 1}^{n} d_{i j}^{2}) \\ = - \frac{1}{2} (d_{i j}^{2} - d_{i \cdot}^{2} - d_{\cdot j}^{2} + d_{\cdot \cdot}^{2}) \end{aligned}$

$M$

这样我们就可以通过矩阵 $D$

因为B是对称的矩阵，所以可以通过特征分解得到：

$\begin{aligned} B & = V Λ V^{- 1} \\ = V Λ V^{T} \end{aligned}$

$M$

此时我们选择前 $p$

$\begin{aligned} B^{*} = V^{*} Λ^{*} V^{* T} \\ V^{*} (n \times p), Λ^{*} (p \times p) \end{aligned}$

$M$

$\begin{aligned} B^{*} & = V^{*} {Λ^{*}}^{\frac{1}{2}} * {Λ^{*}}^{\frac{1}{2}} V^{* T} \\ = X^{*} {X^{*}}^{T} \end{aligned}$

$M$

$X^{*} = V^{*} {Λ^{*}}^{\frac{1}{2}}$

$M$

MDS的例子

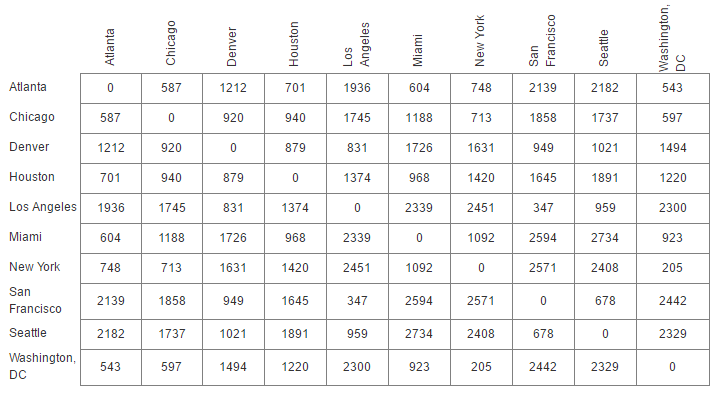
举个例子：拿美国一些大城市之间的距离作为矩阵传进去，简单写一写代码：
```
import numpy as np
import matplotlib.pyplot as plt

def mds(D,q):
    D = np.asarray(D)
    DSquare = D**2
    totalMean = np.mean(DSquare)
    columnMean = np.mean(DSquare, axis = 0)
    rowMean = np.mean(DSquare, axis = 1)
    B = np.zeros(DSquare.shape)
    for i in range(B.shape[0]):
        for j in range(B.shape[1]):
            B[i][j] = -0.5*(DSquare[i][j] - rowMean[i] - columnMean[j]+totalMean)
    eigVal,eigVec = np.linalg.eig(B)
    X = np.dot(eigVec[:,:q],np.sqrt(np.diag(eigVal[:q])))

    return X


D = [[0,587,1212,701,1936,604,748,2139,2182,543],
[587,0,920,940,1745,1188,713,1858,1737,597],
[1212,920,0,879,831,1726,1631,949,1021,1494],
[701,940,879,0,1374,968,1420,1645,1891,1220],
[1936,1745,831,1374,0,2339,2451,347,959,2300],
[604,1188,1726,968,2339,0,1092,2594,2734,923],
[748,713,1631,1420,2451,1092,0,2571,2408,205],
[2139,1858,949,1645,347,2594,2571,0,678,2442],
[2182,1737,1021,1891,959,2734,2408,678,0,2329],
[543,597,1494,1220,2300,923,205,2442,2329,0]]

label = ['Atlanta','Chicago','Denver','Houston','Los Angeles','Miami','New York','San Francisco','Seattle','Washington, DC']
X = mds(D,2)
plt.plot(X[:,0],X[:,1],'o')
for i in range(X.shape[0]):
    plt.text(X[i,0]+25,X[i,1]-15,label[i])
plt.show()
```
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
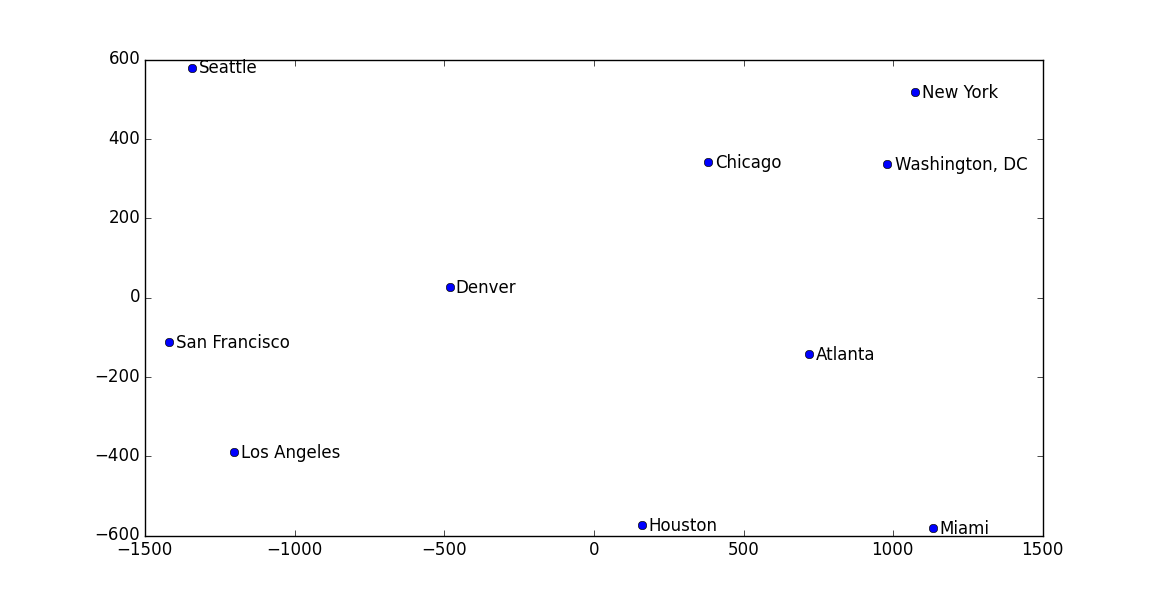
最后画出来的图中，各个城市的位置和真实世界中的相对位置都差不多:

注意，这个例子中其实也有‘流形’在里面，因为我们的地球其实是一个三维，而城市间距离刻画的是在球面上的距离，所以最后如果你去看求出来的特征值，并不像前面说的那样只有q个非0的值。

reference
查看全文

相关阅读:
支付宝生活号授权获取用户信息
 jQuery选项卡
 多图上传加验证加修改file样式
 微信小程序上传图片单张
 圣诞节的整理前两周的内容5
圣诞节的整理前两周的内容4
圣诞节的整理前两周的内容3
圣诞节的整理前两周的内容2
圣诞节的整理前两周的内容1
2018.12.14——函数作用域

原文地址：https://www.cnblogs.com/xiaoxuesheng993/p/9649289.html

维度打击，机器学习中的降维算法：ISOMAP & MDS

流形学习

ISOMAP

经典MDS（Multidimensional Scaling）

MDS的例子

reference