最近公共祖先

 

最近公共祖先

PS：

如果一棵二叉树的结点要么是叶子结点，要么它有两个子结点，这样的树就是满二叉树。

若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

等比数列通项公式、求和公式

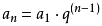
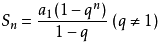
then，看题

x的祖先是 a ,a可以有很多，从x到1路径上的所有点都是它的祖先

对于两个点x,y，位置不同，向上跳到父节点，直到相遇，第一个相遇的点就是lca

题目计算的是任意两个点 LCA 的深度，这个数量等于，任意两个点公共的祖先共有多少个。

显然成立

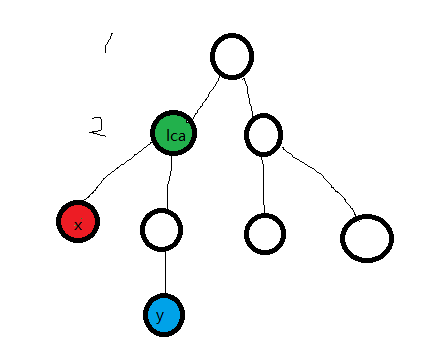
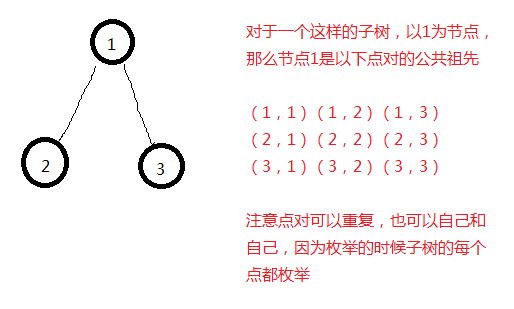
 任意两个点x,y的公共祖先是a的话，等价于x，y都在a的子树里,也就是相当于a是点对（x,y）的公共祖先，全部寻找完之后，会发现还有其他的点对的公共祖先是a,也就是a还是其他点对的公共祖先，问题就转化为枚举每个节点a,看它是多少个点对的公共祖先

比如我们枚举x,y,有多少个公共祖先a

 

换一下枚举顺序就是

注意到没有必要将所有点对的 LCA 都计算出来，因为对于同一层的两个节点lca是相同的，每一层只需要算一个节点就行

 考虑计算第 i 层的某个节点，是多少个点对的公共祖先，这个数量就是该节点子树内节点数的平方。

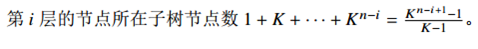(等比数列求和）

是每个a的点对的个数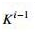，是第i层有多少个点

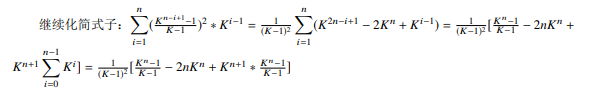
#include <bits/stdc++.h>

using namespace std;

const int mod = 998244353;
typedef long long LL;
int fpm(int p, int k)
{
    int res = 1;
    for (p %= mod; k; k >>= 1, p = (LL) p * p % mod)
        if (k & 1) res = (LL) res * p % mod;
    return res;
}
int main()
{
//    freopen("lca.in", "r", stdin);
//    freopen("lca.out", "w", stdout);
    int n, K; cin >> n >> K;
    int e = fpm(K - 1, mod - 2); //(K - 1) ^ (-1)
    int x = (fpm(K, n) - 1) * (LL) e % mod; //(K ^ n - 1) / (K - 1)
    int ans = (fpm(K, n + 1) + 1) * (LL) x % mod;
    ans = (ans - 2 * n * (LL) fpm(K, n)) % mod;
    ans = ans * (LL) e % mod * (LL) e % mod;
    cout << (ans < 0 ? ans + mod : ans);
}

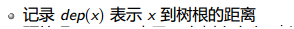（带边权的距离）

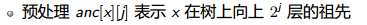
   x在树上向上1层的祖先就是它的父节点

 x在树上向上 j 层的祖先就是 x 向上 ２^{j - 1} 层的祖先向上 ２^{j - 1} 层的祖先

（比如：ａｎｃ［ｘ］［２］＝ａｎｃ［　ａｎｃ［ｘ］［１］　］［１］

　　　　x在树上向上２^２层的祖先就是 x 向上 ２^１ 层的祖先向上 ２^１ 层的祖先）

 

举个栗子：

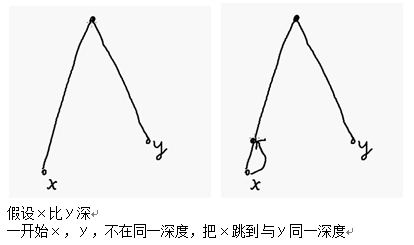
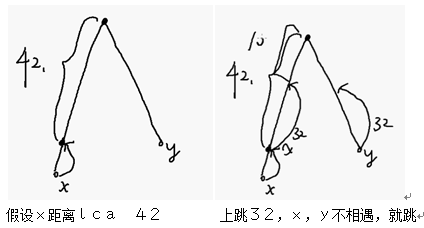
 由于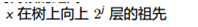

 

（代码等着补上）