LCA 最近公共祖先
局限于树,倍增大法好
Part 1 定义LCA
LCA:对于一棵有根树,若结点z既是x的祖先,也是y的祖先,那么z就是结点x和y的公共祖先。
PS:祖先不只是父亲,还有爷爷,曾爷爷,曾曾曾爷爷。。。。
我们有一棵树,定义某个点的祖先为这个点到根节点的路径上的所有点
在 x , y 的公共祖先中,深度最大的一个结点,叫做x,y的最近公共祖先,记为 LCA(x , y)
一旦找到LCA,他们的所有公共祖先都可找到,LCA一定是最深的公共祖先
用途:找任意两点的最短路,A --> LCA + B --> CA
Part 2 步骤
步骤:
- 如果A的深度小于B的深度,就把他们交换(只是为了方便处理,跳较深的)
If( depA<depB) swap(A,B)
2. 把A,B调到同一深度
3. A,B同时上调直到A=B,找到LCA
复杂度是O(dep)的,但是如果你的树是一条链,那么还不如不用
Part 3 优化
P[x][i],x的向上第 2^i 辈祖先,也就是从x向根节点走 2^i 步到达的结点
P[x][i] = P[P[x][i-1]][i-1]
(1) 优化:把A,B调到同一深度
我们发现A和B之间有深度差
比如 d[A] - d[B] = 19
二级制分解19
19=10011
A --> P[A][4] 16
A --> P[A][1] 2
A --> P[A][0] 1
(2) 优化:A,B同时上调
一开始A,B的祖先一直不一样,直到某个点,往后就都一样了
我们不好确定最早的相同祖先的点,但是我们可以找到最后一组不相同祖先的 x , y,那么此时,他们的父亲就会是LCA(因为他们离LCA的距离总能被二进制分解啊)
for(i= 20~0)
If(f[A][i]!=f[B][i])
A,B同时上跳2^i
复杂度O(logn)
int lca(int x,int y) { if(dep[x]<dep[y]) swap(x,y); for(int i=20;i>=0;i--) { if(dep[f[x][i]]>=dep[y]) x=f[x][i]; if(x==y) return x; } for(int i=20;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; }
Part 4 注意预处理
为什么数组设置 f [ ][21] 呢???
每个节点只需要用到 0~20 就好了
因为最坏的情况是一条链,节点数不会超过1e6,所以0~20就够了
void pre(int u,int fa) { dep[u]=dep[fa]+1; //子节点深度比父亲大一 for(int i=0;i<20;i++) //处理u的2^k辈祖先 f[u][i+1]=f[f[u][i]][i]; for(int i=head[u];i;i=edge[i].nxt ) { int v=edge[i].to ; if(v==fa) continue; f[v][0]=u; //v的父节点是u pre(v,u); //递归处理儿子 } }
Part 5 code
P3379 【模板】最近公共祖先(LCA)

#include<iostream> #include<cstdio> #include<string> #include<cstring> #include<cmath> #include<algorithm> #include<queue> #include<cstdlib> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } const int maxn=5e5+10; int n,m,s,edge_num=0; int head[maxn*2],dep[maxn],f[maxn][21]; struct node { int nxt,to; }edge[maxn*2]; void addedge(int u,int v) { edge[++edge_num].to =v;edge[edge_num].nxt =head[u];head[u]=edge_num; edge[++edge_num].to =u;edge[edge_num].nxt =head[v];head[v]=edge_num; } void pre(int u,int fa) { dep[u]=dep[fa]+1; for(int i=0;i<20;i++) f[u][i+1]=f[f[u][i]][i]; for(int i=head[u];i;i=edge[i].nxt ) { int v=edge[i].to ; if(v==fa) continue; f[v][0]=u; pre(v,u); } } int lca(int x,int y) { if(dep[x]<dep[y]) swap(x,y); for(int i=20;i>=0;i--) { if(dep[f[x][i]]>=dep[y]) x=f[x][i]; if(x==y) return x; } for(int i=20;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; } int main() { n=read();m=read();s=read(); int x,y; for(int i=1;i<n;i++) { x=read();y=read(); addedge(x,y); } pre(s,0); for(int i=1;i<=m;i++) { x=read();y=read(); printf("%d ",lca(x,y)); } return 0; }
Part 6 LCA应用:
处理树上可以差分的信息
用到树上求A到B的最短路径:A -> 根 + B -> 根 - 2 * LCA -> 根
例题
题解
显然这道题的主要内容在于怎样判断树上路径是否相交
树上的路径要么是倒立的 V 形,要么是一条链
对于每个a,b,c,d
先求出来 lca1 = lca ( a , b ) , lca2 = lca ( c , d )
如果 lca1 == lca2 ,那么显然仓鼠和基友会在lca处相遇
否则 如果 dep[ lca1 ] == dep[ lca2 ] ,一定不会有相交,just like this
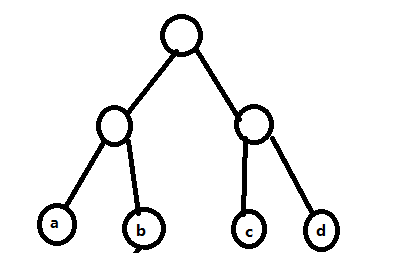
下面分类讨论:
(1)lca1 的深度比较浅,如果路径相交一定是这种情况:
a 或者 b 中任意一个结点与 lca2 的 LCA 是 lca2
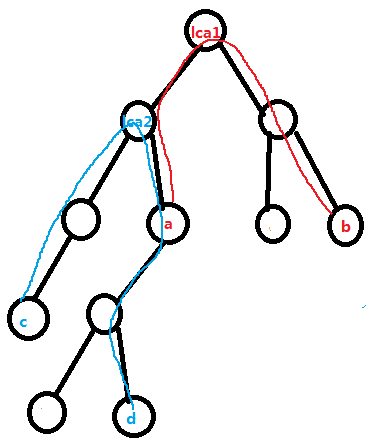

(2)lca2 比较浅的情况同理
代码

#include<iostream> #include<cstdio> #include<string> #include<cstring> #include<cmath> #include<algorithm> #include<cstdlib> #include<queue> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } const int maxn=1e5+10; int n,q,edge_num=0; int head[maxn*2],dep[maxn],f[maxn][21]; struct node { int nxt,to; }edge[maxn*2]; void addedge(int u,int v) { edge[++edge_num].nxt =head[u];edge[edge_num].to =v;head[u]=edge_num; edge[++edge_num].nxt =head[v];edge[edge_num].to =u;head[v]=edge_num; } void pre(int x,int fa) { dep[x]=dep[fa]+1; f[x][0]=fa; for(int i=0;i<20;i++) f[x][i+1]=f[f[x][i]][i]; for(int i=head[x];i;i=edge[i].nxt ) { int y=edge[i].to ; if(y==fa)continue; f[y][0]=x; pre(y,x); } } int lca(int x,int y) { if(dep[x]<dep[y]) swap(x,y); for(int i=20;i>=0;i--) { if(dep[f[x][i]]>=dep[y]) x=f[x][i]; if(x==y) return x; } for(int i=20;i>=0;i--) { if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; } return f[x][0]; } bool check(int a,int b,int c,int d) { int lca1=lca(a,b),lca2=lca(c,d); if(lca1==lca2) return 1; if(dep[lca1]==dep[lca2]) return 0; if(dep[lca1]<dep[lca2]) { if(lca(lca2,a)==lca2) return 1; if(lca(lca2,b)==lca2) return 1; } if(dep[lca1]>dep[lca2]) { if(lca(lca1,c)==lca1) return 1; if(lca(lca1,d)==lca1) return 1; } return 0; } int main() { n=read();q=read(); int x,y; for(int i=1;i<n;i++) { x=read();y=read(); addedge(x,y); } pre(1,0); for(int i=1;i<=q;i++) { int a,b,c,d; a=read();b=read();c=read();d=read(); if(check(a,b,c,d)) printf("Y "); else printf("N "); } return 0; }
PS:一开始是倒着想哪些情况不可以,然后写锅了,感谢hmr大佬提供的思路
