学习最小生成树算法之前我们先来了解下下面这些概念:
树(Tree):如果一个无向连通图中不存在回路,则这种图称为树。
生成树 (Spanning Tree):无向连通图G的一个子图如果是一颗包含G的所有顶点的树,则该子图称为G的生成树。生成树是连通图的极小连通子图。这里所谓极小是指:若在树中任意增加一条边,则将出现一条回路;若去掉一条边,将会使之变成非连通图。
最小生成树(Minimum Spanning Tree,MST):或者称为最小代价树Minimum-cost Spanning Tree:对无向连通图的生成树,各边的权值总和称为生成树的权,权最小的生成树称为最小生成树。常用于网络构建等建设性问题的优化。
构成生成树的准则有三条:
1、 必须只使用该网络中的边来构造最小生成树。
2、必须使用且仅使用n-1条边来连接网络中的n个顶点
3、不能使用产生回路的边。
构造最小生成树的算法主要有:克鲁斯卡尔(Kruskal)算法和普利姆(Prim)算法他们都遵循以上准则。
克鲁斯卡尔算法的基本思想是以边为主导地位,始终选择当前可用(所选的边不能构成回路)的最小权植边。所以Kruskal算法的第一步是给所有的边按照从小到大的顺序排序。这一步可以直接使用库函数qsort或者sort。接下来从小到大依次考察每一条边(u,v)。
具体实现过程如下:
1、设一个有n个顶点的连通网络为G(V,E),最初先构造一个只有n个顶点,没有边的非连通图T={V,空},图中每个顶点自成一格连通分量。
2、在E中选择一条具有最小权植的边时,若该边的两个顶点落在不同的连通分量上,则将此边加入到T中;否则,即这条边的两个顶点落到同一连通分量 上,则将此边舍去(此后永不选用这条边),重新选择一条权植最小的边。
3、如此重复下去,直到所有顶点在同一连通分量上为止。

1 import java.util.ArrayList; 2 import java.util.Collections; 3 import java.util.HashMap; 4 import java.util.HashSet; 5 import java.util.List; 6 import java.util.Map; 7 import java.util.Set; 8 9 public class Kruskal { 10 private final List<Edge> edgeList; 11 private final int n;//总顶点数 12 13 private Set<Edge> T = new HashSet<>();//生成树的边集 14 private Map pntAndNode = new HashMap(); 15 16 public Set<Edge> getT() { 17 buildMST(); 18 return T; 19 } 20 21 public Kruskal(List<Edge> edgeList, int n) { 22 this.edgeList = edgeList; 23 //为每个顶点建立一个并查集的点 24 for (Edge edge : edgeList) { 25 pntAndNode.put(edge.getStart(), new UnionFind.UFNode()); 26 pntAndNode.put(edge.getEnd(), new UnionFind.UFNode()); 27 } 28 this.n = n; 29 } 30 31 public static void main(String[] args) { 32 List<Edge> edgeList = build(); 33 Kruskal obj = new Kruskal(edgeList, 5); 34 // obj.buildMST(); 35 for (Edge e : obj.getT()) { 36 System.out.println(e); 37 } 38 } 39 40 private static List<Edge> build() { 41 List<Edge> l = new ArrayList<>(); 42 l.add(new Edge("C", "D", 1)); 43 l.add(new Edge("C", "A", 1)); 44 l.add(new Edge("C", "E", 8)); 45 l.add(new Edge("A", "B", 3)); 46 l.add(new Edge("D", "E", 3)); 47 l.add(new Edge("B", "C", 5)); 48 l.add(new Edge("B", "E", 6)); 49 l.add(new Edge("B", "D", 7)); 50 l.add(new Edge("A", "D", 2)); 51 l.add(new Edge("A", "E", 9)); 52 53 return l; 54 } 55 56 /*构建MST的核心方法*/ 57 private void buildMST() { 58 Collections.sort(edgeList);//排序 59 //迭代 60 for (Edge e : edgeList) { 61 if (!ok(e)) 62 continue; 63 //确认过了,就把边都加入 64 T.add(e); 65 66 if (T.size() == n - 1) 67 return;//生成树的边数==总顶点数-1 =》 所有点都已经连接 68 } 69 } 70 71 //并查集中查询e 的起点和终点是否在一个集中 72 private boolean ok(Edge e) { 73 UnionFind.UFNode x = (UnionFind.UFNode) pntAndNode.get(e.getStart()); 74 UnionFind.UFNode y = (UnionFind.UFNode) pntAndNode.get(e.getEnd()); 75 if (UnionFind.find(x) != UnionFind.find(y)) {//在不同的集中 76 UnionFind.union(x, y);//合并并返回true 77 return true; 78 } 79 return false; 80 } 81 82 }
最关键的地方在于“连通分量的查询和合并”,需要知道任意两个点是否在同一连通分量中,还需要合并两个连通分量。这个问题正好可以用并查集完美的解决
并查集(Union-Find set)这个数据结构可以方便快速的解决这个问题。基本的处理思想是:初始时把每个对象看作是一个单元素集合;然后依次按顺序读入联通边,将连通边中的两个元素合并。在此过程中将重复使用一个搜索(Find)运算,确定一个集合在那个集合中。当读入一个连通边(u,v)时,先判断u和v是否在同一个集合中,如果是则不用合并;如果不是,则用一个合并(Union)运算把u、v所在集合合并,使得这两个集合中的任意两个元素都连通。因此并查集在处理时,主要用到搜索和合并两个运算。
为了方便并查集的描述与实现,通常把先后加入到一个集合中的元素表示成一个树结构,并用根结点的序号来表示这个集合。因此定义一个parent[n]的数组,parent[i]中存放的就是结点i所在的树中结点i的父亲节点的序号。例如,如果parent[4]=5,就是说4号结点的父亲结点是5号结点。约定:如果i的父结点(即parent[i])是负数,则表示结点i就是它所在的集合的根结点,因为集合中没有结点的序号是负的;并且用负数的绝对值作为这个集合中所含结点的个数。例如,如果parent[7]=-4,说明7号结点就是它所在集合的根结点,这个集合有四个元素。初始时结点的parent值为-1(每个结点都是根结点,只包含它自己一个元素)。
实现并查集数据结构主要有2个函数。

1 import java.util.HashSet; 2 import java.util.Set; 3 4 public class UnionFind { 5 6 public static UFNode find(UFNode x) { 7 UFNode p = x; 8 Set<UFNode> path = new HashSet<UFNode>(); 9 // 记录向上追溯的路径上的点 10 while (p.parent != null) { 11 path.add(p); 12 p = p.parent; 13 } 14 // 这些点的parent全部指向这个集的代表 15 for (UFNode ppp : path) { 16 ppp.parent = p; 17 } 18 // root 19 return p; 20 21 } 22 23 public static void union(UFNode x, UFNode y) { 24 find(y).parent = find(x); 25 } 26 27 public static class UFNode { 28 UFNode parent; 29 } 30 }
最后贴出边集的代码

1 /** 2 * 边 的封装 3 * 边集可以用来表示图 4 */ 5 public class Edge<T> implements Comparable<Edge> { 6 private T start; 7 private T end; 8 private int distance; 9 10 public Edge(T start, T end, int distance) { 11 this.start = start; 12 this.end = end; 13 this.distance = distance; 14 } 15 16 public T getStart() { 17 return start; 18 } 19 20 public void setStart(T start) { 21 this.start = start; 22 } 23 24 public T getEnd() { 25 return end; 26 } 27 28 public void setEnd(T end) { 29 this.end = end; 30 } 31 32 public int getDistance() { 33 return distance; 34 } 35 36 public void setDistance(int distance) { 37 this.distance = distance; 38 } 39 40 @Override 41 public String toString() { 42 return start + "->" + end + ":" + distance; 43 } 44 45 @Override 46 public int compareTo(Edge obj) { 47 int targetDis = obj.getDistance(); 48 return distance > targetDis ? 1 : (distance == targetDis ? 0 : -1); 49 } 50 }
最后运行Kruskal类的结果为:
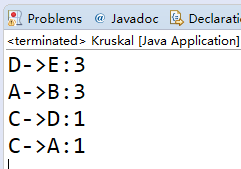
例题:POJ- 1287,蓝桥杯-城市建设。
