最近天下有一种颇不太平的感觉,各地的乱刀砍人,到处是贪官服法。京东准备上市了,阿里最近也提交申请了,猎豹也逆袭了,据说猎豹移动在国际市场上表现甚是抢眼。只有屌丝还在写着代码。花开花又谢,花谢花又开,为什么这么多人没有安全感呢?是转型社会给大家带来了浮躁,还是什么?不得而知!
另外,就上一篇文章的问题,还请大家各抒己见!一道面试题:C++相比C#或者java的优势到底在哪里
OK,下面进入今天的主题。红黑树。
我们时候用到了红黑树?
C++STL中map,set的底层实现全是用的红黑树,java,C#等语言同样如此。
为什么需要红黑树?
map,set底层都提供了排序功能,且查找速度快。红黑树实际上是AVL的一种变形,但是其比AVL(平衡二叉搜索树)具有更高的插入效率,当然查找效率会平衡二叉树稍微低一点点,毕竟平衡二叉树太完美了。但是这种查找效率的损失是非常值得的。它的操作有着良好的最坏情况运行时间,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n是树中元素的数目。
何为红黑树?
这里二叉平衡树的概念我就不提了。红黑树是每个节点都带有颜色属性的二叉查找树,颜色或红色或黑色。
操作:
我们知道平衡二叉树要保持他的平衡性,旋转是一项必不可少的工作。同样,红黑树是一颗准平衡二叉树,旋转也是一项重要工作。旋转有向左旋转,向右旋转,左右旋转,右左旋转。其实左右和右左旋转就是左、右旋转的二次使用,我们这里只谈论向左旋转、向右旋转。
树的旋转:
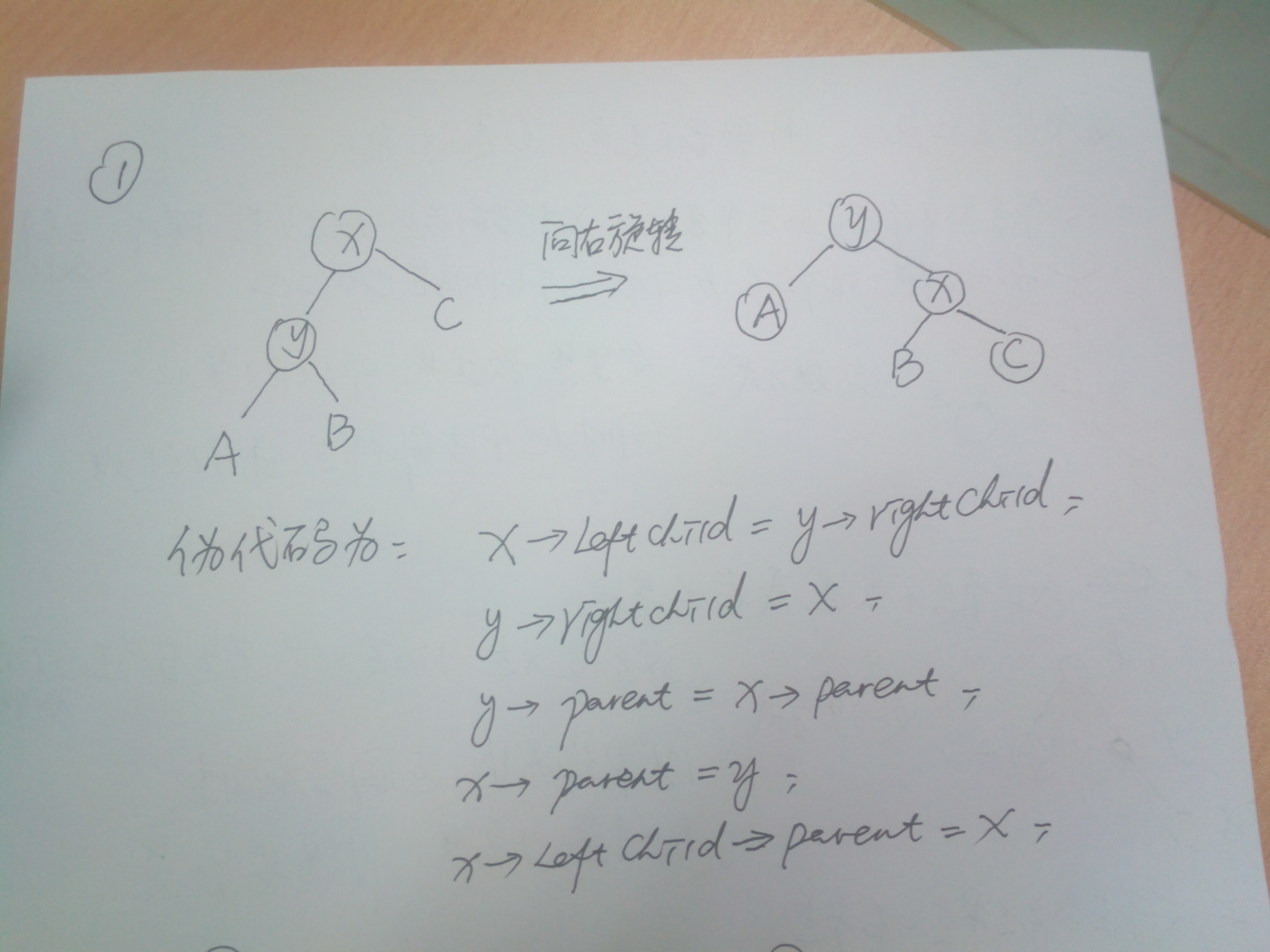
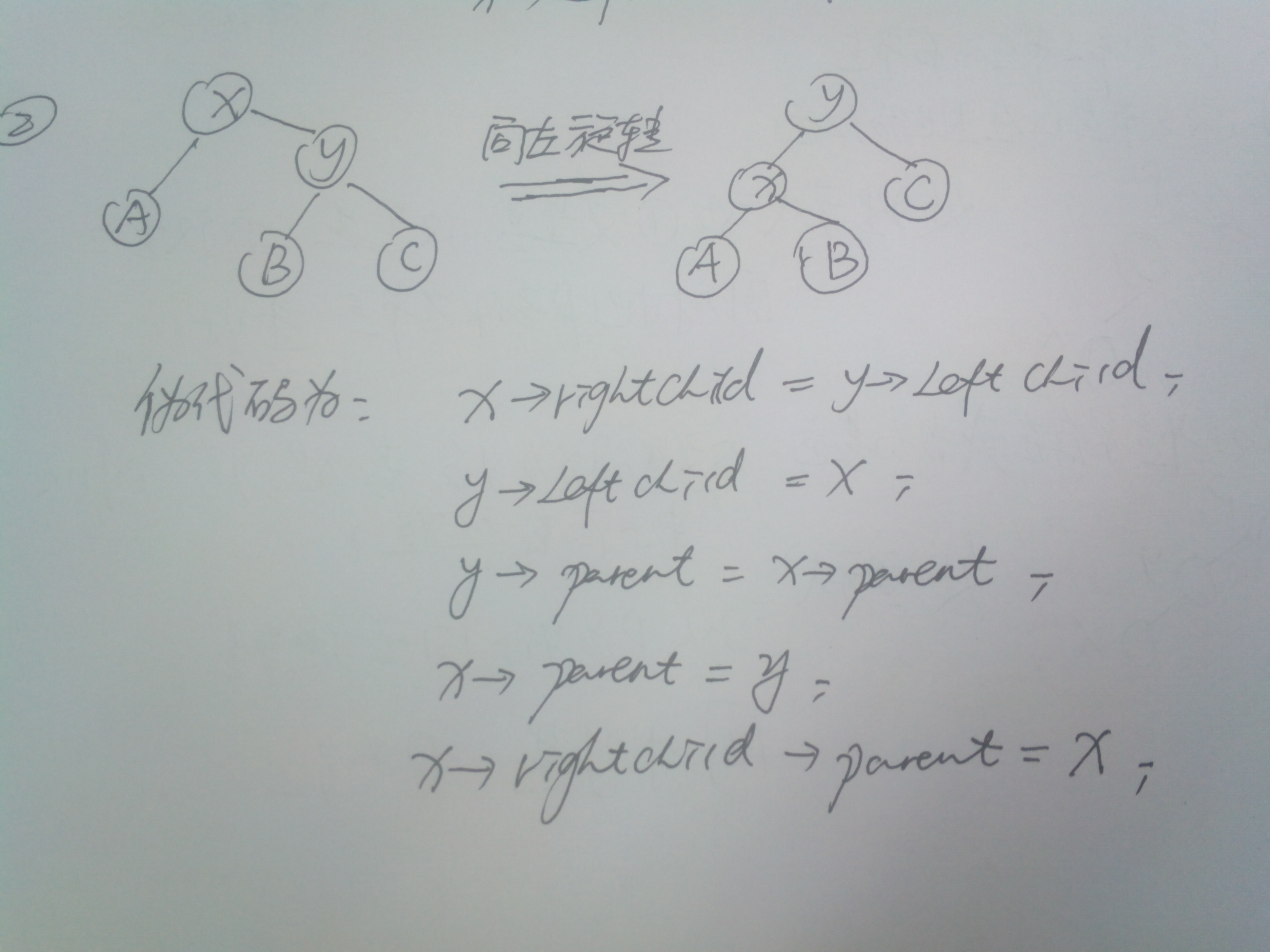
左右旋转的就是上图所示了,代码如下:
1 void leftRoate(rbTreeNode* x){//左旋转
2 rbTreeNode* y=x->right;
3 y->parent=x->parent;
4 if (x->parent==NULL)
5 root=y;
6 x->right=y->left;
7 if (y->left!=NULL)
8 y->left->parent=x;
9 if (x->parent!=NULL&&x->parent->left==x){
10 x->parent->left=y;
11 }else if (x->parent!=NULL&&x->parent->right==x){
12 x->parent->right=y;
13 }
14 y->left=x;
15 x->parent=y;
16 }
17 void rightRoate(rbTreeNode* x){//右旋转
18 rbTreeNode* y=x->left;
19 x->left=y->right;
20 y->parent=x->parent;
21 if (x->parent==NULL)
22 root=y;
23 if (x->left!=NULL)
24 x->left->parent=x;
25 if (x->parent!=NULL&&x->parent->left==x){
26 x->parent->left=y;
27 }else if (x->parent!=NULL&&x->parent->right==x){
28 x->parent->right=y;
29 }
30 y->right=x;
31 x->parent=y;
32 }
红黑树的插入:
一直搜查到叶子节点X,X的父节点会出现以下几种情况:
1、父节点是空,或者父节点的颜色是黑色。直接插入。
2、父节点是红色:
1)父节点是爷爷结点的左结点
a,叔叔结点存在,且是红色
b,叔叔结点不存在,或者是黑色
2)父节点是爷爷结点的右孩子
c,叔叔结点存在且也为红色
d,叔叔结点不存在,或者为黑色。

第二种情况:

红黑树的插入操作就是上图所示:代码如下,
1 void keepRBTreeBlance(rbTreeNode* x,rbTreeNode* y){
2 x->color=red;
3 while(x!=NULL&&x->parent!=NULL&&x->parent->color==red){//父节点是红色
4 if (x->parent==x->parent->parent->left){//父节点是爷爷结点的左节点
5 rbTreeNode* z=x->parent->parent->right;//叔叔结点
6 if(z&&x->parent->color==red){//叔叔结点存在,且也为红色。父和叔都置黑,爷爷置红。
7 x->parent->color=black;//父置黑
8 z->color=black;//shushu置黑
9 x->parent->parent->color=red;//爷爷置红
10 x=x->parent->parent;
11 }else{//叔叔结点时黑色或者叔叔结点不存在的情况。
12 if (x==x->parent->right){//////........................问题
13 //rbTreeNode* temp=x;
14 x=x->parent;
15 leftRoate(x);
16 }
17 x->parent->color=black;
18 x->parent->parent->color=red;
19 rightRoate(x->parent->parent);
20 }
21 }else if (x->parent==x->parent->parent->right){//父节点是爷爷结点的右节点
22 rbTreeNode* z=x->parent->parent->left;//叔叔结点
23 if (z&&z->color==red){//都是红色
24 x->parent->color=black;//父置黑
25 z->color=black;//shushu置黑
26 x->parent->parent->color=red;//爷爷置红
27 x=x->parent->parent;
28 }else{
29 if (x==x->parent->left){//如果是左孩子,需要一次右转身跳投
30 x=x->parent;
31 rightRoate(x);
32 }
33 x->parent->color=black;//同时改变颜色。
34 x->parent->parent->color=red;
35 leftRoate(x->parent->parent);
36 }
37 }
38 }
39 root->color=black;
40 }
41
42 bool insertRBTree(elemType elemValue){
43 rbTreeNode* y=header;
44 rbTreeNode* x=root;
45 while(x!=NULL){
46 y=x;
47 if (elemValue>x->data){//elemValue大于该节点的值,转右子树
48 x=x->right;
49 }else if (elemValue<x->data){//elemValue小于该节点的值,转左子树
50 x=x->left;
51 }else if (elemValue==x->data){//有相等的直接返回false
52 return false;
53 }
54 }
55 rbTreeNode* z=new rbTreeNode();
56 z->data=elemValue;
57 if (y==header){//空直接插入
58 z->color=black;
59 root=z;
60 return true;
61 }else{
62 if (y->data>elemValue)
63 y->left=z;
64 else
65 y->right=z;
66 }
67 z->parent=y;
68 keepRBTreeBlance(z,y);
69 return true;
70 }
红黑树的删除操作类似于B-树的删除,需要注意保持它的红黑平衡性。红黑的搜索那就和B-树的查找一模一样了,其实任何排序树的操作都是一样的。比如下面将要讲到的B+树。
B树系列还有一篇是B+树,敬请期待。
参考文献:STL源码剖析、百度。
版权所有,欢迎转载,但是转载请注明出处:潇一