基于视频结构化的应用中,目标在经过跟踪算法后,会得到一个唯一标识和它对应的运动轨迹,利用这两个数据我们可以做一些后续工作:测速(交通类应用场景)、计数(交通类应用场景、安防类应用场景)以及行为检测(交通类应用场景、安防类应用场景)。我会写三篇文章依次介绍这三个主题。
(1)目标跟踪之速度计算
(2)目标跟踪之计数
(3)目标跟踪之行为检测
后面会陆续添加链接。
本篇文章以交通类应用场景为例,介绍车辆速度计算方法。
速度计算前提
速度=距离÷时间
视频是一个连续的图片序列,我们只要分别知道目标在第N帧和第M帧中的位置(像素坐标),然后这两帧之间的时间间隔,就可以得到目标在视频图像中的“像素速度”(像素/秒),计算方式很简单:
像素速度=像素距离÷时间
其中像素距离可以通过目标在两帧中对应的像素坐标计算得到(X1-X2)+(Y1-Y2),又由于视频帧率比较固定,一般视频FPS为25,那么每帧时间为40ms,(M-N)*40即为目标从N帧中位置移动到M帧中位置耗费的时间。如果我们又知道视频画面中每像素代表的实际物理距离(米),那么最终的目标运动速度就非常好计算了。
但是,由于摄像机在拍摄三维空间画面成像时,会存在透视。假设目标在三维空间的路面直线运动,由远到近(反之亦然),即使目标的实际运动速度固定不变,我们在视频画面观察到的像素速度却是在不断变化的,而且这个变化并不呈线性关系。换句话说,视频画面中每像素代表的实际距离并不固定:
实际物理速度!=像素速度*某值
这个问题就非常麻烦了,由于视频画面中的像素距离和实际物理距离不存在线性对应关系,我们不能简单通过目标的像素坐标和时间间隔来计算目标的实际运动速度。
两种解决方案:
1)虽然像素距离和实际物理距离不存在简单的线性对应关系,但是我们可以加入其他条件值,找出像素距离和实际物理距离的映射关系,比如目标由远及近,当视频画面累计运动5像素时,实际累计运动距离为5米,当视频画面累计运动10像素时,实际累计运动距离为8米,以此类推。找到这种映射关系的前提是需要加入其他条件值,比如摄像机与地面的垂直高度等,见后面“视频测速通常做法”。
2)通过变换,将视频画面转换成“俯视视角”(站在道路上方俯视道路)。经过这种变换之后,路面所有的运动目标都可以看作是2D平面运动,变换之后的每像素所代表的实际物理距离固定不变(米/像素)。这样一来,计算实际物理速度就非常简单了,先计算像素速度,然后再乘以一个固定值即可得到实际物理速度。这种画面转换也需要提供一些参数,但是相比第1)种,参数来源简单许多。
视频车辆测速通常做法
常见的视频测速做法是,根据一系列参数,比如摄像机距离地面的垂直高度、摄像机焦距等,来计算两帧之间车辆的实际物理位移差,再除以两帧之间的时间,得到车辆的形式速度。该方式的前提是需要知道每个测量位置摄像机的属性参数,而现实中获取这些参数非常困难:
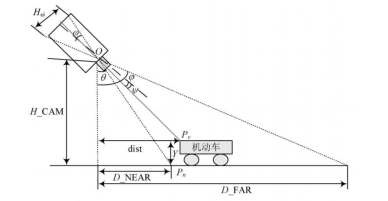
如上图,根据摄像机成像原理,三维空间在二维画面上投影之后,会存在对应角度关系,可以列出等式,计算机动车在路面行驶的实际距离。这种做法的前提是我们必须知道图中的H_CAM(摄像机距离地面的高度)、D_NEAR(摄像机成像最近点与摄像机垂直线之间的水平距离)以及D_FAR(摄像机成像最远点与摄像机垂直线之间的水平距离),而这些参数获取在现实应用场景中基本不可能做到。
另外一些视频测速的方式跟上面差不多,只是需要的参数有些差异,比如不需要D_NEAR和D_FAR的值,但是必须知道摄像机的焦距等参数,这些参数也是非常难以得到。
基于透视变换的车辆测速方法
前面提到过,如果将视频画面转换成俯视图,视角垂直于路面,这样能保证画面中每像素所代表的实际物理距离固定不变。任何目标运动速度都可以根据像素位移差和时间差计算得到。这种做法的前提是,如何将任意视频画面转换成俯视图?
熟悉OpenCV的童鞋可能知道,OpenCV中有透视转换的概念,如果我们知道原视频画面中一个真实矩形的四个顶点坐标,那么我们可以直接利用这四个顶点来计算图像的透视转换矩阵(原图->俯视图),得到透视转换矩阵后,我们就可以将源视频画面的任意一个点坐标转换成俯视图中的点坐标。假设源视频画面中,目标第N帧的坐标为(Xn、Yn),目标第M帧的坐标为(Xm、Ym),那么经过转换之后,在俯视图画面中,目标第N帧的坐标为(Xn`, Yn`),目标第M帧的坐标为(Xm`, Ym`),假设在短时间内,目标车辆沿道路方向做直线匀速运动,那么最终的Xn` 和 Xm`的值应该相等(水平位移分量为零),而(Ym` - Yn`)的值即为目标车辆沿道路方向行驶的像素距离,前面说到过,俯视图中的每像素距离代表的实际物理距离是固定不变的(假设为W),那么我们很容易得到目标车辆沿道路方向行驶的实际物理距离,即为 (Ym` - Yn`)*W。然后将得到的结果再除以N帧到M帧之间的时间 (M-N)*40ms,就可以得到目标车辆在这段时间内的平均速度(米/秒),如果M和N相差很小,假设相隔5帧,那么这个速度即可代表目标车辆的实时车速了。
上面这种测速方式的前提有两个:
(1)知道路面上一个真实矩形在源视频画面中的四个顶点坐标
(2)知道俯视图中每像素代表的实际物理距离
第(1)个前提相比获取摄像机与地面的垂直高度而言,要简单得多。实际应用场景中,路面有非常多的参照物可以来确定一个真实的矩形四个顶点坐标。第(2)个也比较容易,一般车道分割线都是由实线-虚线间隔而成的,而实线的长度是固定的(高速公路一般实线长度为6米),我们只需要在源视频画面中标定一根实线线段的起始点坐标即可,假设为(X1, Y1), (X2, Y2),通过转换矩阵将其转换成俯视图中的坐标,假设为(X1`, Y1`), (X2`, Y2`),由于车道分割线的方向与道路方向一致,那么X1`和X2`理论上应该相等(水平分量为零),6米/ (Y2` - Y1`)即可以代表俯视图中(车道方向)每像素代表的实际物理距离。
下图选取了路面中一个实际矩形在源视频画面中的四个顶点(红色),以及一个车道分割线参照线段的两个端点(黄色):

经过透视变换之后:

可以看到,经过透视变换之后生成的俯视图中,我们将路面的矩形还原成了“真正的”矩形,并且可以看到,车道分割线是均匀分布的,两条分割线也是平行的,这符合我们的预期,即:俯视图中,无论是道路的平行方向,还是道路的垂直方向,每像素所代表的实际物理距离是固定不变的。目标车辆在俯视图中,只会存在与道路平行方向的位移差,与道路垂直方向的分量为零,这符合俯视角度观察到的结果。
注意:需要忽略其他与道路不在同一个平面上的物体,这种透视变换只对道路平面有效。
另外再举一个摄像机角度比较好的例子:

上图是选取的矩形四个顶点,下图是透视变换之后的俯视图:

经过转换之后生成的俯视图,可以作为矩形标注的参考,如果发现生成的俯视图完全不对,那么说明标注的矩形四个顶点坐标有问题。
经过实际使用发现,这种测速误差在±6%之内,这种准确性虽然不能用于交通执法,但是对于交通状况监测还是非常有参考价值的。当然这种方法也有劣势:
(1)参考矩形不太好标注,有的路面甚至没有任何参照物。完全靠经验去尝试;
(2)有的路面没有距离参照物,比如不存在车道分割线(虚线),这种情况无法测速;
(3)测速结果的准确性对参照物的标注依赖很大,后者直接影响测速结果。
当然,它的优势前面已经提到了。本文只提供思路,没有代码。