感知机
要理解svm,首先要先讲一下感知机(Perceptron),感知机是线性分类器,他的目标就是通过寻找超平面实现对样本的分类;对于二维世界,就是找到一条线,三维世界就是找到一个面,多维世界就是要找到一个线性表达式,或者说线性方程:
f(x) = ΣθiXi
表达式为0,就是超平面,用来做分界线作为分类;A分类都满足f(x) > 0, B分类都满足f(x) < 0;未来进行分类预测的时候,就是将特征值带入到模型中,根据输出值的正负号即可实现分类。算法实现过程即使初始化一个权重矩阵,然后通过梯度下降来进行持续优化。
但是感知机有一个问题:那就是解太多了,比如二维世界里面(元素只有两个特征),作为区分线可以划分无数条:
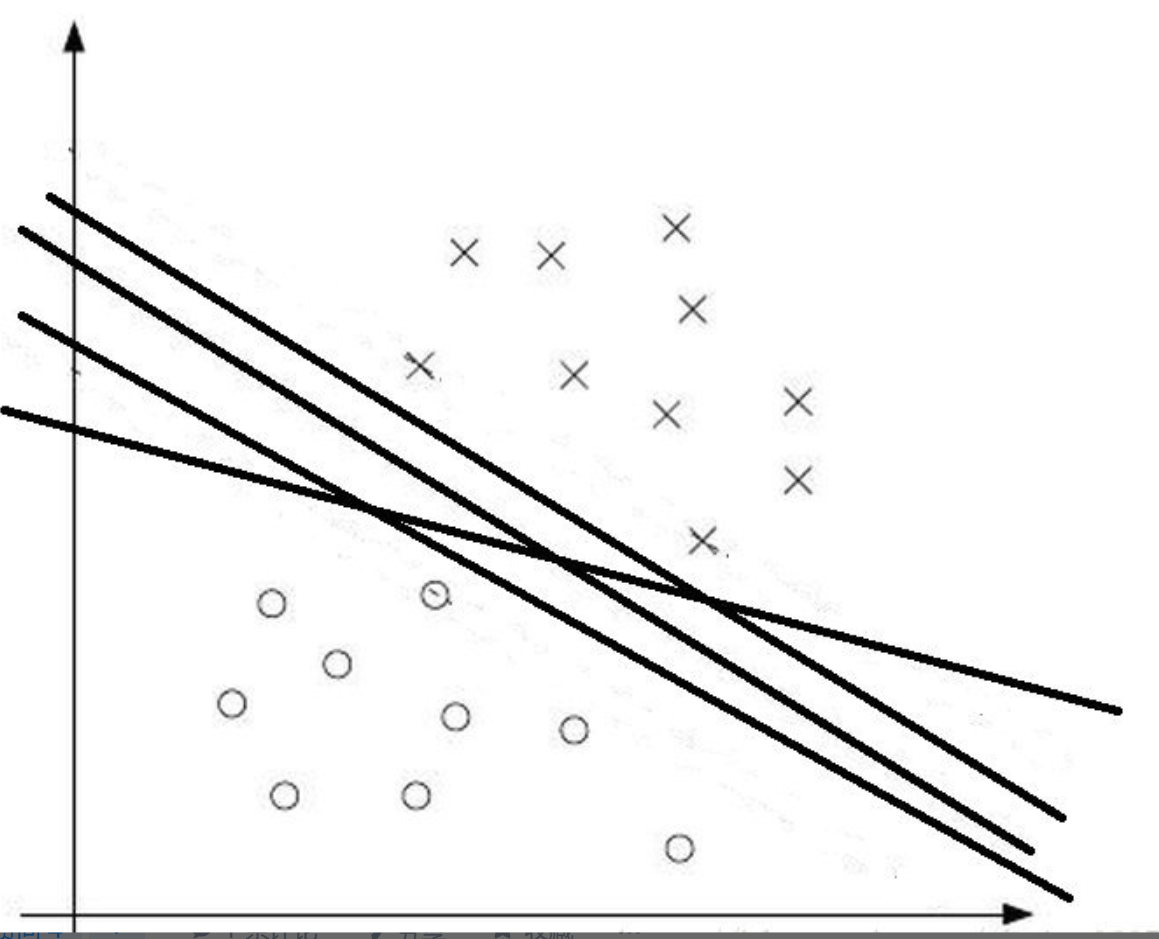
所以现在使用感知机来进行数据分类的已经很少了,但是感知机确实很多优秀机器学习的基础,比如神经网络,以及今天我们要讲的SVM。
SVM的支持平面和超平面
SVM基于感知机的理论有深入了一步,就是SVM追求,距离超平面最近的点的距离最大化,或者说追求分类超平面两面的支持平面的宽度尽量宽:

为什么呢?我们先来讲一下为什么叫支持向量机,就是因为,SVM关注的是超平面两边的"支持"超平面,及所谓辅助超平面,那么在支持超平面上面的点呢,因为是方向和大小的,所以称之为支持向量,所以在构建出来的模型称之位"支持向量机(SVM,Support Vector Machine)"。
那么为什么要最大化呢?其实最大化就是指最近的两类元素之间的距离最小化(max 1/||w|| 等价于min 0.5 *||w||²(这里的0.5其实可以不管,因为不影响对于w取值),所以两个分类元素之间最小距离,就是要找的两个支持平面的距离;支持两个平面(包含了支持向量)的最大化,其实意味着超平面是位于最中间的位置;这个最中间的位置,是值得玩味的,因为如果有偏倚的话,将会导致分类偏差,如下图所示,蓝线和橙色的线,明显有偏离,这样对导致分类偏差:

所以,我们目标是能够将超平面建立在中间位置,那么怎么确定这个中间位置呢?这个时候就需要获取最近分类元素之间距离,这个距离就是最大距离,然后依赖这些元素,构建两条平行的支持(辅助)超平面,而是可以推出超平面(等距的夹在两个支持超平面之间)。
这两个支持超平面分别f(x) = 1以及f(x) = -1,不要问我为什么是1或者-1,因为没有为什么,只是习惯;这个比较像逻辑回归,为什么区分要是(0,1),其实(-1,1)可以,只要模型能够把元素的类别分出来,其实模型区分度具体的值并不重要,我们指定了具体的值,只不过是希望模型能够唯一化,否则有无数个模型取值可以满足样本划分了;
所以,只要是能够实现符号相反就可以,总之就是一条辅助超平面罩着的小弟满足函数值 > 0,另外一条支持超平面罩着的"小弟"的函数值<0即可。
那么怎么来计算距离呢?什么是距离?曼哈顿,欧式等等,其实距离本身就是一个元素特征某种算法,比如可以哈希算法,可以是直接加减,还可以是某个既有特征权重,比如对于函数距离而言,就是y * (wx + b),简写成y * f(x),这里的y是样本分类真值(1,或者-1),为什么这么做?y值为1,并不会改变距离值本身,这里,函数距离有一个好处,就是符号性,如果f(x)预测正确,那么y和f(x)符号一致结果必然是正值,如果是负值,说明预测错误。不过函数距离有一个问题,就是当w和b同步缩放的时候,会导致距离变化,但是其实这种等比变化其实是一个平面;所以最终采用的集合距离:
y * (wx + b)/ ||w||
注:这个公式来自于空间距离公式d = |Ax + By + Cz|/(A² + B² + C²)^0.5
下面就是求解最大距离问题,首先是要进行变形,因为i我们目标是求解w,所以其实对于距离公式而言,所以我们可以假设分子为1或者分母为1,因为在求极值的场景下,它是不影响的,svm选择分子为1(感知机选择分母为1)。于是目标就是:
max 1 / ||w||
对于这个max过程的求解使用了动态规划里面的凸优化算法,这里强调一下动态规划,就是都在变,支持向量在变,支持超平面在变(w,b不定),超平面也在变,这个是动态规划范畴,凸优化是因为解决这个问题满足了凸优化的拉格朗日算法求解。
结果就是可以计算出来w和b。通过w和b,我们可以知道那些是模型的支持向量,支持超平面以及超平面都可以知道了。
软间隔 - SVM对于异常点的处理
为了避免少量的异常点导致的街道距离变宽,所以采用了软间隔(相对于上面介绍的硬间隔),就是允许部分异常点在街道里面,同时还能够正确分类这些街道内的值;至于允许多少,SVM中通过一个参数C来进行控制,称之为惩罚系数,这个C越大,意味着惩罚越大,可以理解为比较严格,对于异常点的容忍度也就低;所以街道宽度倾向于窄一些;C小,则意味着SVM设置的相对宽松,允许街道深处存在异常点。
我们可以想象一下,指定了软间隔的svm的街道一定比只是硬间隔的svm的街道要款,只要是软间隔,就一定能够宽容;但是要知道,控制软间隔街道宽度还有一个元素,就是j,优化对象是:
min 1/||w|| + C*∑εi
所以距离是C和j共同的;但是作为超参数,只是提供了C这个接口,我们可以不关ε心,它其实代表的是松弛因子,是每一个元素(样本计算距离的时候都需要考虑的)。
SVM的损失函数
SVM的损失函数称之为合页损失函数(hinge loss function),分类正确且距离大于等于1,那么损失值为0,反之则值是1 - y*(w * x + b);这个计算就是节点到平面1的距离,svm损失函数的目标就是所有的算错的点的到达1的距离最小(这个和感知机的是一样的)
类似的,感知机的损失函数是y *(w*x + b),注意,感知机并没有支持平面,所以也就没有被1减;逻辑回归的损失函数是log[1 - exp(-y * (w*x + b))],上述积累模型的损失函数都是和超平面有关系,可能是因为都是分类模型,最求的都是针对超平面距离最小化的处理吧。
代码处理
在使用scikit learn里面的linearSvc的时候,注意以下三个函数:
C:惩罚系数
loss:损失函数,需要指定为"hinge",默认的不是这个。
dual:特征数量>样本数量,true;反之,false
但是,这个只是线性SVM,因为做分类是线性表达式(平面),那么那些非平面的分类怎么办呢?SVM可是号称全能分类小能手啊。请见下一篇,SVM核函数
参考: