norm代表的是距离,两个向量的距离;下图代表的就是p-norm,其实是对向量里面元素的一种运算;
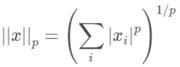
最简单的距离计算(规范)是欧式距离(Euclidean distance),两点间距离是如下来算的,属于L2-norm:
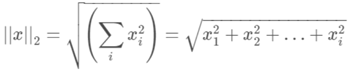
另外一种就是出租车距离(也称之为曼哈顿距离):这是一种1-norm:
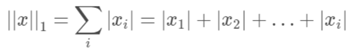
L1-norm对应的就是1-norm,L2-norm对应的是2-norm;
注意上面的x代表的是两个向量的差值,x=v1-v2;x1=v1【1】-v2【1】。
下面的就是岭回归(L2-norm)和Lasso回归(L1-norm)的成本公式:

在健壮性上面(抵御异常值),L1是优于L2的,因为L1是线性的,L2是曲线,后者对于离群值(outlier)的判断是要更加困难的;
在稳定性上面(水平调整的抵抗力,和健壮性相反),L2是优于L1的;
在解决方案层面上,L2只有一个,比如欧氏距离中,因为是多元的,所以当且仅当x和y同时满足才能够实现距离最短(比如线性回归里面的梯度下降,里面就是对x,y同时求导);但是,L1只有则有多个解,下面的就是曼哈顿路线图,可以看到其实是有多条路可以到对角。
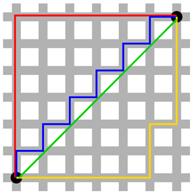
计算困难度上面,L2是要高于L1,毫无疑问,L2是平方计算,L1是一次方计算;
稀疏性(Sparsity)上面,L1要高于L2的;
这里讲述的L1,L2其实是扩展讲述,其实在岭回归以及Lasso回归中重要的应用场景是如果线性回回模型导致了过拟合,此时需要进行正则化,这个时候可以选择岭回归和Lasso回归来进行正则化,所谓的正则化其实就是讲规则公式增加一些噪声,其中就是通过添加L1或者L2的噪声。