解题报告:
题目大意:现有一个蜜蜂房如右图所示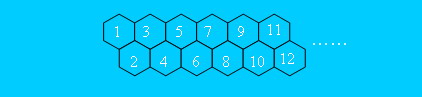 ,每一个蜜蜂房都有编号,现在一只蜜蜂要从a号蜜房爬到b号蜜蜂房,问一共有多少条不同的路线。
,每一个蜜蜂房都有编号,现在一只蜜蜂要从a号蜜房爬到b号蜜蜂房,问一共有多少条不同的路线。
又是一道动态规划题,由于整个蜂房是按照一定的周期排列的,所以我们可以不管a和b到底是多少,只要知道b-a的值就可以了,为了方便,令n=b-a,即要求蜜蜂从1号蜂房走到n号蜂房一共有多少种不同的路线,我们可以将1到n转化为1到n-1和1到n-2的子问题来求出我们所要的解,可以理解为当现在要从一号房爬到n号房,可以假设蜜蜂现在在n-1号房,那么蜜蜂从n-1号房爬到n号房可以有一种走法,另一种是假设蜜蜂现在就在n-2号房,那么从n-2号房走到n号房也是只有一种走法所以只要将这两种子问题的解的种数加起来,便得到走到n号房的路线种数,因为只有从n-1和n-2号这两个蜂房才可以直接走到n号蜂房,所以只需要分析这两种子问题就够了,递推公式是DP[n]=DP[n-1]+DP[n-2]。
 View Code
View Code
1 #include<stdio.h> 2 __int64 DP[55]; 3 void dabiao(void) { 4 DP[1]=1,DP[2]=2; 5 for(int i=3;i<=51;++i) 6 DP[i]=DP[i-1]+DP[i-2]; 7 } 8 int main() { 9 int T,a,b; 10 dabiao(); 11 scanf("%d",&T); 12 while(T--) { 13 scanf("%d%d",&a,&b); 14 printf("%I64d\n",DP[b-a]); 15 } 16 return 0; 17 }
