《自动化技术中的进给电气运动》
阅读内容:第1.3节
知识要点:
本节主要以不可调节电气传动系统为例,介绍了系统在时间域的静态和动态特性以及电气系统对于简单信号的响应。
1.采用微分方程分析系统
对于只有一个输入和输出的线性系统都可表示成如下的微分方程形式。其中u为输入,v为输出,且对于实际系统有m≤n。
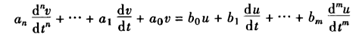
以不可调电气传动系统为例,列出系统的机械和电气微分方程。
(1)JGes=JM+JL
(2)uA-eM=RAiA+LAdiA/dt
(3)eM=cMωM
(4)MM=ML+MB=ML+JGesdωM/dt
(5)MM=cMiA
(6)MB=JGesdwM/dt
经过整合和化简后得到如下简图(实际上一个可以组合成不止一种系统框图,即便是同样的微分方程组):
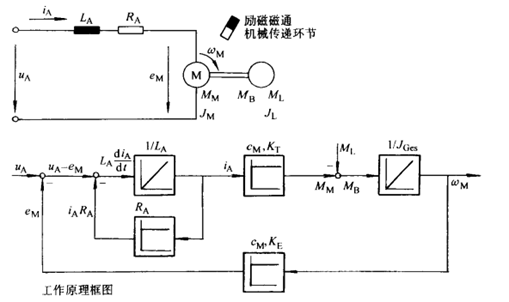
联立(2)(3)(4)(5)并引入传动系统电气时间常数Tel A,并进行定标处理,得到系统的二阶微分方程
(7)
(I)t=0时刻,利用极限研究法推导上微分方程,根据规律得知,此时当出现一个输入量跃变时输入量表现出一个有限的上升速度。即启动瞬时角速度ωM从一个稳定值转变成另一个稳定值。
(2)考虑t趋近于0时,上式中关于t的导数项变为0,得到
(8)
结论:对于一个不可调速系统,系统稳定时一个接入的负载转矩会产生一个角速度的固定偏差。
2.系统的动态响应
这里要注意的是过渡函数的概念,在教材中有关于过渡过程的介绍:当系统中电动机的转矩或者负载转矩发生变化的时候,系统经历的一个稳定运转状态变化到另一个稳定状态的变化过程。而这里过渡函数的概念是针对于输出信号的变化与输入跃变的高度联系在一起行成的。对于阶跃响应,若Tel A远小于Tmech A,ML=0,
(7)式化简为
(9) ,
,
由微积分知识可以得到此方程的解,
(10)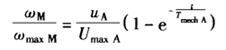
其实按照简化的微分方程式也可以得知此时参数的变化特征是一阶延时系统。
使用过原点的切线求得的时间常数往往不准确,可以采用测量一个瞬时值并带入上式计算的方法求解。
斜坡响应适用于大惯量的系统或者在阶跃信号可能会引发危险性振荡,并且微分特性只能采用斜坡响应测量出来。单位脉冲响应的可以用来测量积分系统,同时可以用来得出简单系统的传递函数。
主要难点:
a.采用微分方程简化的方法分析系统的特性需要一定的数学功底,特别是针对部分必要参数的简化。
b.关注自己研究的参数之间的方程联系,可能只需要等效成一个二阶甚至是一阶系统,但是可能遗漏参数之间的相互影响。
《控制系统设计指南》
阅读内容:第一、二章
知识要点:
这两个章节是控制理论和频域研究方法的简介。控制系统主要分为一个控制律与功率变换器,控制系统一方面按照需要改变系统的状态,另一方面又要克服扰动。采用频域研究的方法避免了对复杂微分方程的求解,使得微分方程组变成了频域分析的工具。我们通常分析的系统都是线性系统,具有均一性、叠加性、时不变性。但是许多元器件并不是线性元件,这时候就需要采用补偿环节以减小非线性环节对系统分析造成的影响。系统主要的性能指标有增益和相位,这些在频域分析的时候通常采用Bode图表示。系统对于不同的频率的输入信号的响应的增益不同,通常来说随着输入信号的频率升高,系统的增益逐渐降低,高出一定的频率范围系统甚至会不再响应。
主要疑点:
Ⅰ.将书中电动机的定子作为转子,转子作为定子是否可行?我觉得这样可以使电动机的惯量变大,增大动态转矩。
Ⅱ.可调电气传动系统与不可调电气传动系统的区别是什么?
Ⅲ.(9)式得来的前提条件是假设ML=0,然而此时ML对于时间的微分项不一定也为0,式子(7)中最后一项为什么可以消去?
Ⅳ.时间域研究系统的启动瞬时和稳定状态时相对简单,但是研究任意瞬时的时候就要考虑求解微分方程,这是不是意味着目前还只能通过实验测定而不能预测复杂系统在某个特定时刻的运行状态?