题目要求:
Find the total area covered by two rectilinear rectangles in a 2D plane.
Each rectangle is defined by its bottom left corner and top right corner as shown in the figure.

Assume that the total area is never beyond the maximum possible value of int.
Credits:
Special thanks to @mithmatt for adding this problem, creating the above image and all test cases.
为了更好说明问题,在这里特地画了几个图:
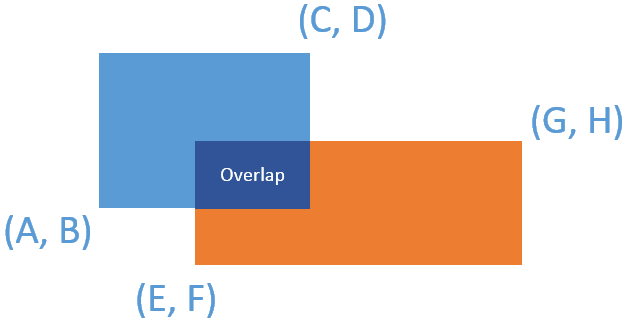
我们要求的面积 = 两个矩形面积和 - 两者重叠部分。
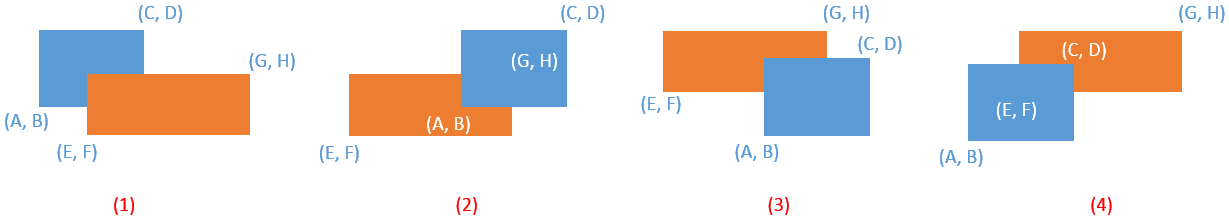
可能出现的四种情况。
根据以上四种可能出现的情况,我们编写程序如下(参考自一博文):
1 class Solution { 2 public: 3 int overlapArea(int A, int B, int C, int D, int E, int F, int G, int H) 4 { 5 int v1 = max(A, E); 6 int v2 = min(C, G); 7 int v = v2 - v1; 8 9 int h1 = max(B, F); 10 int h2 = min(D, H); 11 int h= h2 - h1; 12 13 if(v <= 0 || h <= 0) 14 return 0; 15 else 16 return v * h; 17 } 18 19 int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) { 20 int area1 = (C - A) * (D - B); 21 int area2 = (G - E) * (H - F); 22 int overlapRegion = overlapArea(A, B, C, D, E, F, G, H); 23 return area1 + area2 - overlapRegion; 24 } 25 };