1.Linked List Cycle
题目要求:
Given a linked list, determine if it has a cycle in it.
Follow up:
Can you solve it without using extra space?
刚看到这道题,很容易写出下边的程序:
1 bool hasCycle(ListNode *head) { 2 ListNode *a = head, *b = head; 3 while(a) 4 { 5 b = a->next; 6 while(b) 7 { 8 if(a == b) 9 return true; 10 b = b->next; 11 } 12 a = a->next; 13 } 14 15 return false; 16 }
这个程序最大的问题在于“死循环”,例如在下边这种情况就会进入死循环:

要解决这个问题,我们可以定义两个指针slow、fast,slow每次前进一步,fast每次前进两步。如果链表存在环,则在循环一定次数后,slow与fast一定会重合(找个例子推导下就明白了)。具体从程序如下:
1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode(int x) : val(x), next(NULL) {} 7 * }; 8 */ 9 class Solution { 10 public: 11 bool hasCycle(ListNode *head) { 12 if(head == nullptr || head->next == nullptr) 13 return false; 14 15 ListNode *slow = head, *fast = head; 16 while(fast != nullptr && fast->next != nullptr) 17 { 18 slow = slow->next; 19 fast = fast->next->next; 20 if(slow == fast) 21 return true; 22 } 23 24 return false; 25 } 26 };
2.Linked List Cycle II
题目要求:
Given a linked list, return the node where the cycle begins. If there is no cycle, return null.
Follow up:
Can you solve it without using extra space?
这道题难度还是挺大的。具体解法参考自一博文:
首先看图:
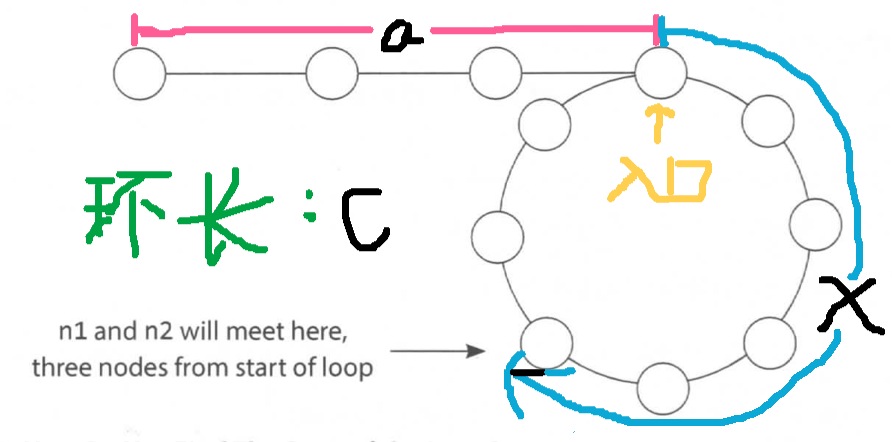
从链表起始处到环入口长度为:a,从环入口到Faster和Slower相遇点长度为:x,整个环长为:c。
假设从开始到相遇,Slower走过的路程长为s,由于Faster的步速是Slower的2倍,那么Faster在这段时间走的路程长为2s。
而对于Faster来说,他走的路程还等于之前绕整个环跑的n圈的路程nc,加上最后这一次遇见Slower的路程s。
所以我们有:
2s = nc + s
对于Slower来说,他走的路程长度s还等于他从链表起始处到相遇点的距离,所以有:
s = a + x
通过以上两个式子代入化简有:
a + x = nc
a = nc - x
a = (n-1)c + c-x
a = kc + (c-x)
那么可以看出,c-x,就是从相遇点继续走回到环入口的距离。上面整个式子可以看出,如果此时有个pointer1从起始点出发并且同时还有个pointer2从相遇点出发继续往前走(都只迈一步),那么绕过k圈以后, pointer2会和pointer1在环入口相遇。这样,换入口就找到了。
具体程序如下:
1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode(int x) : val(x), next(NULL) {} 7 * }; 8 */ 9 class Solution { 10 public: 11 ListNode *detectCycle(ListNode *head) { 12 ListNode* slow = head; 13 ListNode* fast = head; 14 while (true){ 15 if(!fast || !fast->next) 16 return nullptr; 17 18 slow = slow->next; 19 fast = fast->next->next; 20 if (slow == fast) 21 break; 22 } 23 24 slow = head; 25 while (slow != fast){ 26 slow = slow->next; 27 fast = fast->next; 28 } 29 return slow; 30 } 31 };