题目描述
若两个正整数的和为素数,则这两个正整数称之为“素数伴侣”,如2和5、6和13,它们能应用于通信加密。现在密码学会请你设计一个程序,从已有的N(N为偶数)个正整数中挑选出若干对组成“素数伴侣”,挑选方案多种多样,例如有4个正整数:2,5,6,13,如果将5和6分为一组中只能得到一组“素数伴侣”,而将2和5、6和13编组将得到两组“素数伴侣”,能组成“素数伴侣”最多的方案称为“最佳方案”,当然密码学会希望你寻找出“最佳方案”。
输入
有一个正偶数N(N≤100),表示待挑选的自然数的个数。后面给出具体的数字,范围为[2,30000]。
输出
输出一个整数K,表示你求得的“最佳方案”组成“素数伴侣”的对数。
输入描述
1、 输入一个正偶数n
2 、输入n个整数
输出描述
求得的“最佳方案”组成“素数伴侣”的对数。
输入
4
2 5 6 13
输出
2
思路
相关概念
二分图
二分图其实就是在一个图中所有的点可以分为两组,同一组中没有边,所有的边都跨越了两个组。准确的说:把一个图的顶点划分为两个不相交的集合 U 和 V ,且使得每一条边都分别连接 U 、V 中的顶点,如果存在这样的划分,则称此图为二分图。
此外二分图还有一个等价定义是:不含有「含奇数条边的环」的图。
匹配
二分图匹配就是边的集其中任意两条边没有公共顶点。我们定义有:
匹配边、匹配点、非匹配边、非匹配点。
如图:若1—2相连,5—4相连,7—6相连。则显然1—2边、5—4边、7—6边为匹配边,1、2、4、5、6、7为匹配点。剩下的为非匹配点和非匹配边。
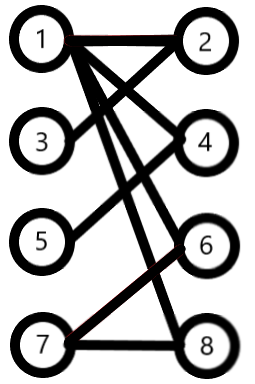
最大匹配
一个图的匹配中所含边数最多的匹配即为此图最大匹配。像上图最大匹配即为:

显然最大匹配可能不只有一种。
完美匹配
如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。上图都是完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
交替路径
从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边……形成的路径叫交替路径。如图2—>1—>8—>7即为一条交替路径。
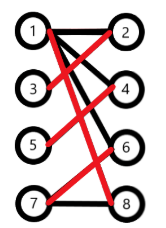
增广路径
从一个未匹配点出发,走交替路径,如果到达另一个未匹配点,则这条交替路径称为增广路径(agumenting path)。如图1—>2—>3—>6—>7—>8即为一条增广路径。
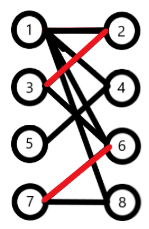
增广路径性质
由增广路的定义可以推出下述三个结论(设当前路径为P,当前匹配为M):
1、P的路径长度必定为奇数,第一条边和最后一条边都不属于M,因为两个端点分属两个集合,且未匹配。
2、P经过取反操作可以得到一个更大的匹配M’。
3、M为G的最大匹配当且仅当不存在相对于M的增广路径。
匈牙利算法:用增广路径求最大匹配
1、置M为空 。
2、找出一条增广路径P,通过取反操作获得更大的匹配M’代替M 3、重复2操作直到找不出增广路径为止 。
寻找增广路径算法
我们采用DFS的办法找一条增广路径,从X部一个未匹配的顶点u开始,找一个未访问的邻接点v(v一定是Y部顶点)。对于v,分两种情况:
1、如果v未匹配,则已经找到一条增广路。
2、如果v已经匹配,则取出v的匹配顶点w(w一定是X部顶点),边(w,v)目前是匹配的,根据“取反”的想法,要将(w,v)改为未匹配,(u,v)设为匹配,能实现这一点的条件是看从w为起点能否新找到一条增广路径P’。如果行,则u-v-P’就是一条以u为起点的增广路径。
代码如下
1 #include<iostream> 2 #include<cstring> 3 #include<vector> 4 using namespace std; 5 const int N = 100, M = 60001; 6 vector<int> g[N]; //二分图 7 int pre[N], nums[N]; //偶数对应的当前奇数匹配点,输入的数 8 bool isPrime[M], flag[N]; //素数对应表,可匹配点是否已匹配 9 //欧拉筛表建立素数对应表 10 void primeTab() { 11 int prime[M], cnt = 0; 12 prime[cnt++] = 2; 13 memset(isPrime, true, sizeof(isPrime)); 14 isPrime[0] = isPrime[1] = false; 15 for (int i = 4; i < M; i += 2) 16 isPrime[i] = false; 17 for (int i = 3; i < M; i += 2) { 18 if (isPrime[i]) 19 prime[cnt++] = i; 20 for (int j = 0; j < cnt && i * prime[j] < M; ++j) { 21 isPrime[i * prime[j]] = false; 22 if (i % prime[j] == 0) 23 break; 24 } 25 } 26 } 27 //深度优先搜索增广路径,从而找到最大匹配 28 bool dfs(int n) { 29 for (int i = 0; i < g[n].size(); ++i) { 30 int x = g[n][i]; 31 if (flag[x]) //若nums[x]是nums[n]已经匹配的点,现在需要将其腾出 32 continue; 33 flag[x] = true; //nums[x]成为nums[n]的匹配点 34 //nums[x]未被匹配||nums[x]已被匹配但可以让其匹配点寻找新的匹配点从而腾出nums[x] 35 if (pre[x] == -1 || dfs(pre[x])) { 36 pre[x] = n; //给nums[n]匹配nums[x] 37 return true; 38 } 39 } 40 return false; 41 } 42 int main() { 43 int n; 44 primeTab(); //建立素数对应表 45 /* 46 pre默认赋为-1而非0,这是因为pre存储的是奇数在nums中的下标。 47 若pre默认赋0则pre[i]=0有两种意义: 48 (1)pre[i]映射到无;(2)pre[i]映射到nums[0]。 49 互相矛盾,故赋-1。 50 */ 51 memset(pre, -1, sizeof(pre)); 52 while (cin >> n) { 53 for (int i = 0; i < n; ++i) 54 cin >> nums[i]; 55 for (int i = 0; i < n - 1; ++i) 56 for (int j = i + 1; j < n; ++j) 57 if (isPrime[nums[i] + nums[j]]) 58 nums[i] & 1 ? g[i].push_back(j) : g[j].push_back(i); //链表法建立二分图,奇数链接偶数可匹配点 59 int ans = 0; 60 for (int j = 0; j < n; ++j) { 61 memset(flag, false, sizeof(flag)); 62 if (dfs(j)) 63 ++ans; 64 } 65 cout << ans << endl; 66 for (int i = 0; i < n; ++i) { //清空二分图映射关系 67 g[i].clear(); 68 } 69 memset(pre, -1, sizeof(pre)); //清空偶数对应的当前奇数匹配点 70 } 71 }