算法初级面试题08——递归和动态规划的精髓、阶乘、汉诺塔、子序列和全排列、母牛问题、逆序栈、最小的路径和、数组累加成指定整数、背包问题

 第八课主要介绍递归和动态规划

 

介绍递归和动态规划

暴力递归：

1，把问题转化为规模缩小了的同类问题的子问题

2，有明确的不需要继续进行递归的条件(base case)

3，有当得到了子问题的结果之后的决策过程

4，不记录每一个子问题的解

 

动态规划

1，从暴力递归中来

2，将每一个子问题的解记录下来，避免重复计算

3，把暴力递归的过程，抽象成了状态表达

4，并且存在化简状态表达，使其更加简洁的可能

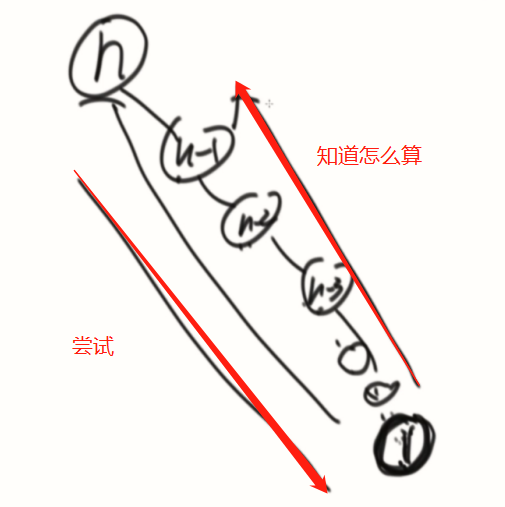
图灵引入的是：我不知道怎么算，但是我知道怎么试。知道怎么暴力破解出来。

要学会，练习懂得怎么尝试。

题目一

求n!的结果

循环是一个知道怎么算的过程（从1乘到n）。

递归是子问题拆分到最小问题的尝试过程。

public class Code_01_Factorial {
    public static long getFactorial1(int n) {
        if (n == 1) {
            return 1L;
        }
        return (long) n * getFactorial1(n - 1);
    }

    public static long getFactorial2(int n) {
        long result = 1L;
        for (int i = 1; i <= n; i++) {
            result *= i;
        }
        return result;
    }

    public static void main(String[] args) {
        int n = 5;
        System.out.println(getFactorial1(n));
        System.out.println(getFactorial2(n));
    }

}

题目二

汉诺塔问题（不能大压小，只能小压大）

打印n层汉诺塔从最左边移动到最右边的全部过程

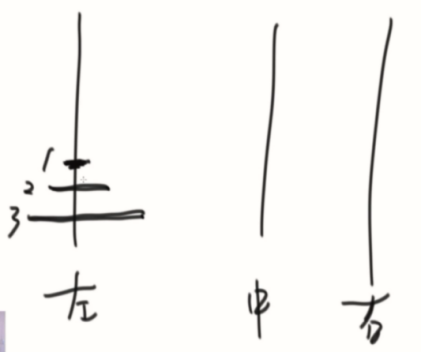
左中右另称为 from、to、help。

划分子问题

1、先把1~n-1从from移动到help

2、把单独的n移动到to

3、1~n-1从help移动到to

时间复杂度就是：

T(n) = T(n-1) + 1 + T(n-1) = 2T(n-1)+1（一个等比公式）

T(n-1)是移动到help

1是从from直接移动到to

T(n-1)是把全部n-1挪回去

总的步数是2的N次方减一

 

这个题目要学会尝试。
也可以写六个移动的递归，来逐一实现步骤。

 

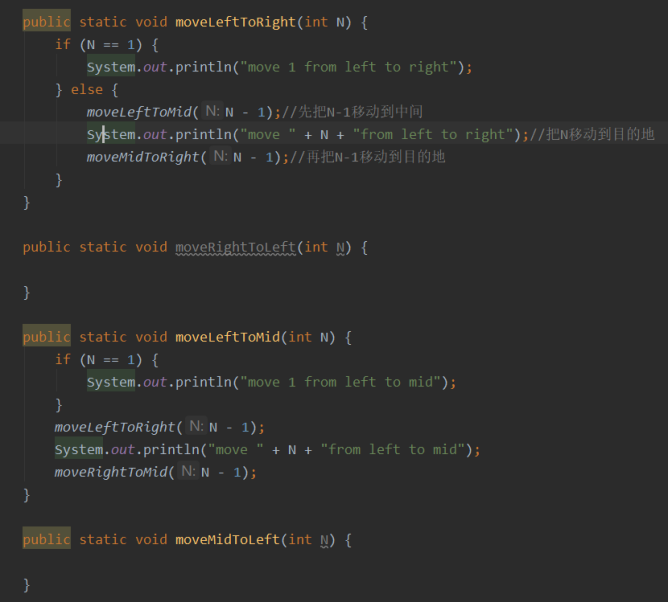
 （该问题最基础的一个模型就是，一个竹竿上放了2个圆盘，需要先将最上面的那个移到辅助竹竿上，然后将最底下的圆盘移到目标竹竿，最后把辅助竹竿上的圆盘移回目标竹竿。）

public class Code_02_Hanoi {

    public static void hanoi(int n) {
        if (n > 0) {
            func(n, n, "left", "mid", "right");
        }
    }

    public static void func(int rest, int down, String from, String help, String to) {
        if (rest == 1) {
            System.out.println("move " + down + " from " + from + " to " + to);
        } else {
            func(rest - 1, down - 1, from, to, help);
            func(1, down, from, help, to);
            func(rest - 1, down - 1, help, from, to);
        }
    }

    //课堂上的代码
    //N 表示当前是 1~N的问题
    //一开始都在from上
    public static void process(int N, String from, String to, String help) {
        if (N == 1) {//就只有一个了，可以直接移动
            System.out.println("Move 1 from " + from + " to " + to);
        } else {//否则就是1~N的问题
            process(N - 1, from, help, to);//把1~N-1个从from移动到help
            System.out.println("Move " + N + " from " + from + " to " + to);//单独把N移动到to
            process(N - 1, help, to, from);//第三步是挪回来,把在help上的挪到to
        }
    }

    public static void moveLeftToRight(int N) {
        if (N == 1) {
            System.out.println("move 1 from left to right");
        } else {
            moveLeftToMid(N - 1);//先把N-1移动到中间
            System.out.println("move " + N + "from left to right");//把N移动到目的地
            moveMidToRight(N - 1);//再把N-1移动到目的地
        }
    }

    public static void moveRightToLeft(int N) {

    }

    public static void moveLeftToMid(int N) {
        if (N == 1) {
            System.out.println("move 1 from left to mid");
        }
        moveLeftToRight(N - 1);
        System.out.println("move " + N + "from left to mid");
        moveRightToMid(N - 1);
    }

    public static void moveMidToLeft(int N) {

    }

    public static void moveRightToMid(int N) {

    }

    public static void moveMidToRight(int N) {
        if (N == 1) {
            System.out.println("move 1 from mid to right");
        }
        moveMidToLeft(N - 1);
        System.out.println("move " + N + "from mid to right");
        moveLeftToRight(N - 1);
    }

    public static void main(String[] args) {
        int n = 3;
        hanoi(n);
    }

}

题目三

打印一个字符串的全部子序列，包括空字符串

怎么把脑里面的尝试变成code，就是写递归的能力

尝试方法：

一开始是空字符串，经过0有两个决定要a和不要a，经过1也要决定要不要b，一直尝试下去，列举所有情况。

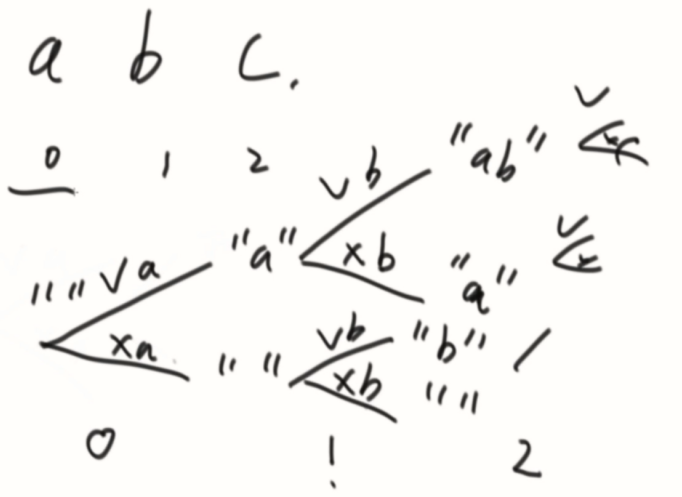
可以画一下你想尝试的图，先来个小规模的，再去写递归就没那么难写了。

 

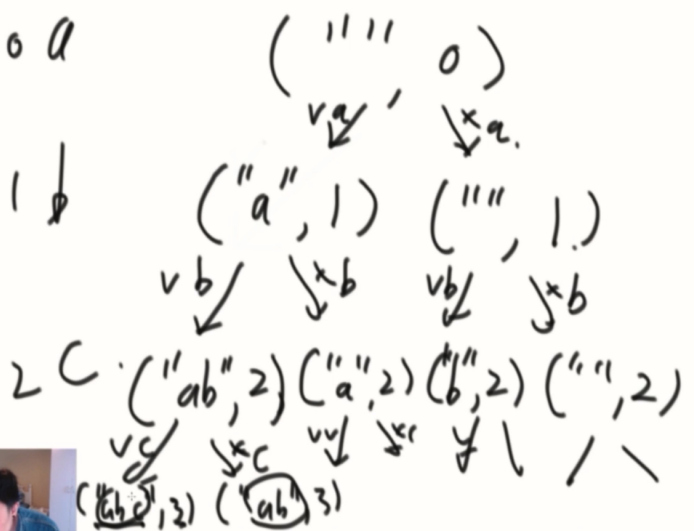
public class Code_03_Print_All_Subsquences {

    public static void printAllSubsquence(String str) {
        char[] chs = str.toCharArray();
        process(chs, 0);
    }

    public static void process(char[] chs, int i) {
        if (i == chs.length) {
            System.out.println(String.valueOf(chs));
            return;
        }
        process(chs, i + 1);
        char tmp = chs[i];
        chs[i] = 0;//用空格代替字符
        process(chs, i + 1);
        chs[i] = tmp;//直接使用字符
    }
    
//    public static void function(String str) {
//        char[] chs = str.toCharArray();
//        process(chs, 0, new ArrayList<Character>());
//    }
//
//    public static void process(char[] chs, int i, List<Character> res) {
//        if(i == chs.length) {
//            printList(res);
//        }
//        List<Character> resKeep = copyList(res);
//        resKeep.add(chs[i]);
//        process(chs, i+1, resKeep);
//        List<Character> resNoInclude = copyList(res);
//        process(chs, i+1, resNoInclude);
//    }
//
//    public static void printList(List<Character> res) {
//        // ...;
//    }
//
//    public static List<Character> copyList(List<Character> list){
//        return null;
//    }

    //课堂上的版本
    public static void printAllSub(char[] str,int i,String res){
        if (i == str.length){//到达字符串的末尾，已经没有选择了
            System.out.println(res);
            return;
        }
        printAllSub(str,i+1,res+" ");//不要当前字符的路
        printAllSub(str,i+1,res+str[i]);//要当前字符的路
    }

    public static void printAllPermutation(){

    }

    public static void main(String[] args) {
        String test = "abc";
        printAllSubsquence(test);
        printAllSub(test.toCharArray(),0,"");
    }

}

题目四

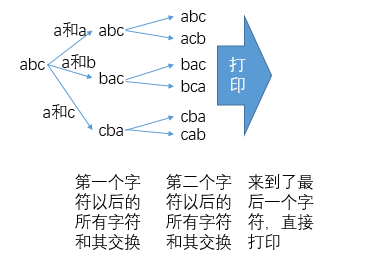
打印一个字符串的全部排列

 

进阶

打印一个字符串的全部排列，要求不要出现重复的排列

public class Code_04_Print_All_Permutations {

    public static void printAllPermutations1(String str) {
        char[] chs = str.toCharArray();
        process1(chs, 0);
    }

    public static void process1(char[] chs, int i) {
        if (i == chs.length) {
            System.out.println(String.valueOf(chs));
        }
        for (int j = i; j < chs.length; j++) {
            swap(chs, i, j);
            process1(chs, i + 1);
            swap(chs, i, j);//回溯
        }
    }

    public static void printAllPermutations2(String str) {
        char[] chs = str.toCharArray();
        process2(chs, 0);
    }

    public static void process2(char[] chs, int i) {
        if (i == chs.length) {
            System.out.println(String.valueOf(chs));
        }
        HashSet<Character> set = new HashSet<>();
        for (int j = i; j < chs.length; j++) {
            if (!set.contains(chs[j])) {
                set.add(chs[j]);
                swap(chs, i, j);
                process2(chs, i + 1);
                //swap(chs, i, j);
            }
        }
    }

    public static void swap(char[] chs, int i, int j) {
        char tmp = chs[i];
        chs[i] = chs[j];
        chs[j] = tmp;
    }

    public static void main(String[] args) {
        String test1 = "abc";
        printAllPermutations1(test1);
        System.out.println("======");
        printAllPermutations2(test1);
        System.out.println("======");

        String test2 = "acc";
        printAllPermutations1(test2);
        System.out.println("======");
        printAllPermutations2(test2);
        System.out.println("======");
    }

}

题目五

母牛每年生一只母牛，新出生的母牛成长三年后也能每年生一只母牛，假设不会死。求N年后，母牛的数量。

一遇到这种递推的题目，不知道怎么试，先列出前几项，递推是有高度结构化的解的。

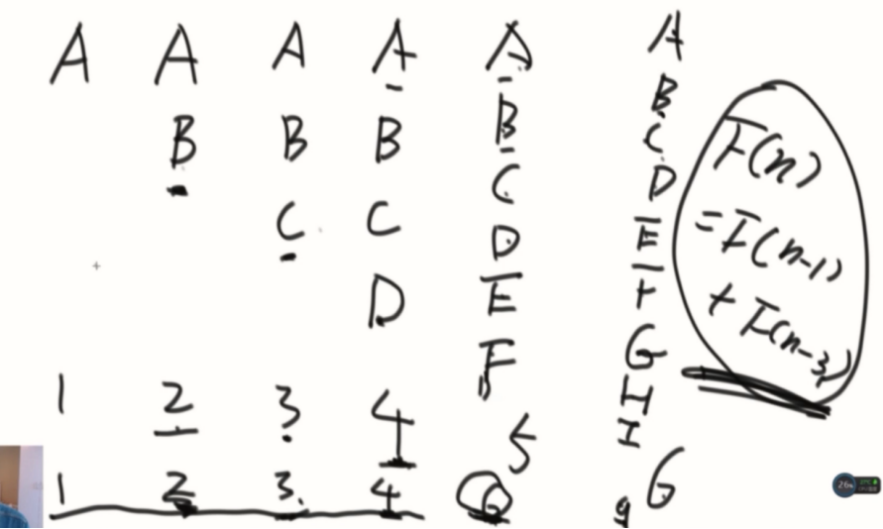
然后要想为什么？

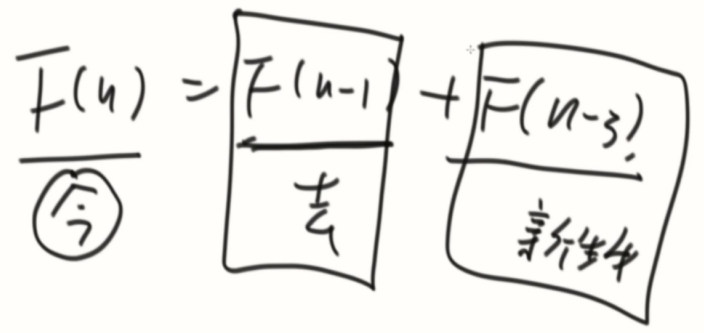
F(n) = F(n-1) + F(n-3)

因为牛都不会死，所以会有去年的牛F(n-1),三年前牛的数量，此时都可以生小牛，所以会有F(n-3)这部分。

 

public class Code_05_Cow {

    public static int cowNumber1(int n) {
        if (n < 1) {
            return 0;
        }
        if (n == 1 || n == 2 || n == 3) {
            return n;
        }
        return cowNumber1(n - 1) + cowNumber1(n - 3);
    }

    //非递归版本
    public static int cowNumber2(int n) {
        if (n < 1) {
            return 0;
        }
        if (n == 1 || n == 2 || n == 3) {
            return n;
        }
        int res = 3;
        int pre = 2;
        int prepre = 1;
        int tmp1 = 0;
        int tmp2 = 0;
        for (int i = 4; i <= n; i++) {
            tmp1 = res;
            tmp2 = pre;
            res = res + prepre;
            pre = tmp1;
            prepre = tmp2;
        }
        return res;
    }

    public static void main(String[] args) {
        int n = 20;
        System.out.println(cowNumber1(n));
        System.out.println(cowNumber2(n));
    }

}

进阶

如果每只母牛只能活10年，求N年后，母牛的数量。

题目六

给你一个栈，请你逆序这个栈，不能申请额外的数据结构，只能使用递归函数。如何实现？

本题考查栈的操作和递归函数的设计，我们需要设计出两个递归函数。

递归函数一：将栈stack 的栈底元素返回并移除。

具体过程就是如下代码中的getAndRemoveLastElement 方法。

如果从stack 的栈顶到栈底依次为3、2、1，这个函数的具体过程如下图所示。

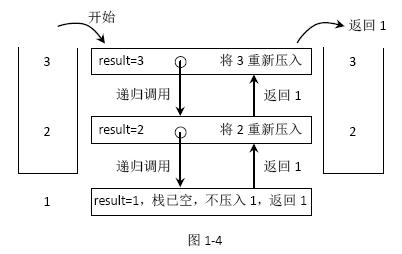
递归函数二：逆序一个栈，就是题目要求实现的方法，具体过程就是如下代码中的reverse方法。该方法使用了上面提到的getAndRemoveLastElement 方法。

如果从stack 的栈顶到栈底依次为3、2、1，reverse 函数的具体过程如图1-5 所示。

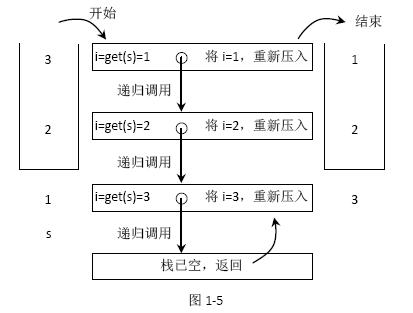
getAndRemoveLastElement 方法在图中简单表示为get 方法，表示移除并返回当前栈底元素。

public class Code_06_ReverseStackUsingRecursive {

    /**
     * 以1，2，3为例，从栈顶到栈底依次为3，2，1
     */
    public static void reverse(Stack<Integer> stack) {
        if (stack.isEmpty()) {
            return;
        }
        int i = getAndRemoveLastElement(stack);//得到栈底元素
        reverse(stack);//递归，所以i依次为1，2，3
        stack.push(i);//回溯，依次压入3，2，1
    }

    //得到栈底元素并它移除，并且其它元素压回栈
    public static int getAndRemoveLastElement(Stack<Integer> stack) {
        int result = stack.pop();
        if (stack.isEmpty()) {
            return result;
        } else {
            int last = getAndRemoveLastElement(stack);
            stack.push(result);//回溯，将其它元素重新压回栈
            return last;//返回栈底元素
        }
    }

    public static void main(String[] args) {
        Stack<Integer> test = new Stack<Integer>();
        test.push(1);
        test.push(2);
        test.push(3);
        test.push(4);
        test.push(5);
        reverse(test);
        while (!test.isEmpty()) {
            System.out.println(test.pop());
        }

    }

}

题目七

给你一个二维数组，二维数组中的每个数都是正数，要求从左上角走到右下角，每一步只能向右或者向下。沿途经过的数字要累加起来。返回最小的路径和。

 

没见过的动态规划有一个统一的套路，写出递归版本尝试版本后，得出来的动态规划的方法是高度套路的。

所有动态规划都是由暴力版本优化来的。

 

问题划分为了：向下或者向右的结果，从中选最小的路径，就是最后的答案。

    //课堂上的代码
    public static int walk(int[][] matrix, int i, int j) {
        int x = matrix.length - 1;
        int y = matrix[0].length - 1;
        if (i == x && j == y) {
            return matrix[i][j];
        }
        if (i == x)//如果i到达行底部，只能向右走。
            return matrix[i][j] + walk(matrix, i, j + 1);

        if (j == y)//如果j到达列边界，只能向下走。
            return matrix[i][j] + walk(matrix, i + 1, j);
        //其他情况，需要对向下和向右进行对比，选出最优解
        int right = walk(matrix, i, j + 1);
        int down = walk(matrix, i + 1, j);
        return matrix[i][j] + Math.min(right, down);

    }

暴力枚举有待优化：有大量的重复解产生，很多部分都重复计算。

把重复计算的部分缓存起来，重复的时候直接调用就能省时间。

 

什么样的尝试版本递归可以改成动态规划？

当把递归过程展开，发现有重复的状态，与到达它的路径是没有关系的，那么它一定能改成动态规划（无后效性问题）。

有后效性的是，汉罗塔、N皇后问题（前面的举动会影响后面的结果）。

 

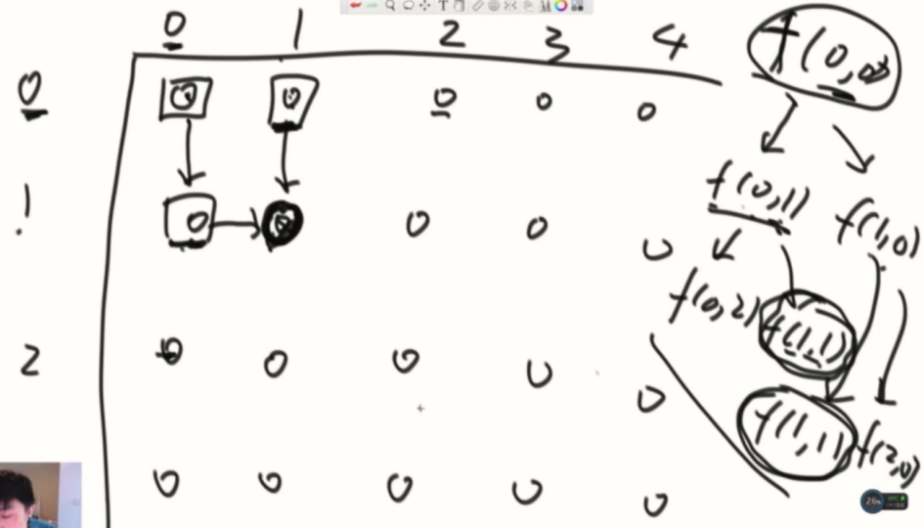
准备一个dp表

1、把需要的位置点出来

2、回到base case中把不被依赖的位置设置好（这题是最后一行/列），然后分析普遍位置是怎么依赖的（需要哪些位置的帮助），反过去就是整个计算顺序。 依次计算，推到顶部就是答案。

 

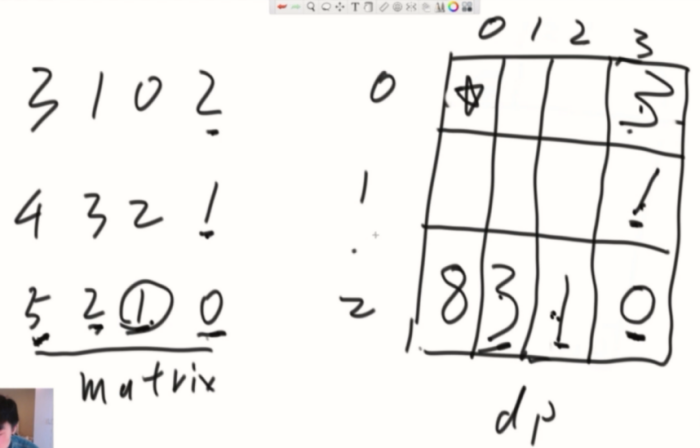
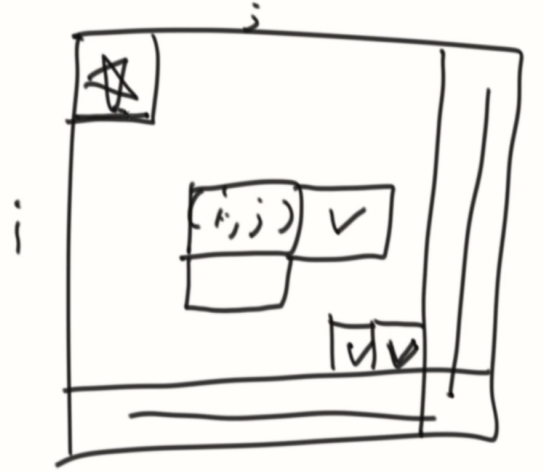
类似一个搭积木的过程，堆积到一定条件就能出现答案。

public class Code_07_MinPath {

    public static int minPath1(int[][] matrix) {
        return process1(matrix, matrix.length - 1, matrix[0].length - 1);
    }

    //从{i,j}出发，到达最右下角位置，最小路径和是多少？
    public static int process1(int[][] matrix, int i, int j) {
        int res = matrix[i][j];
        if (i == 0 && j == 0) {
            return res;
        }
        if (i == 0 && j != 0) {
            return res + process1(matrix, i, j - 1);
        }
        if (i != 0 && j == 0) {
            return res + process1(matrix, i - 1, j);
        }
        return res + Math.min(process1(matrix, i, j - 1), process1(matrix, i - 1, j));
    }
    
    //动态规划
    public static int minPath2(int[][] m) {
        if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
            return 0;
        }
        int row = m.length;
        int col = m[0].length;
        int[][] dp = new int[row][col];
        dp[0][0] = m[0][0];
        //第一列赋值
        for (int i = 1; i < row; i++) {
            dp[i][0] = dp[i - 1][0] + m[i][0];
        }
        //第一行赋值
        for (int j = 1; j < col; j++) {
            dp[0][j] = dp[0][j - 1] + m[0][j];
        }
        //最优赋值
        for (int i = 1; i < row; i++) {
            for (int j = 1; j < col; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + m[i][j];
            }
        }
        return dp[row - 1][col - 1];
    }

    // for test
    public static int[][] generateRandomMatrix(int rowSize, int colSize) {
        if (rowSize < 0 || colSize < 0) {
            return null;
        }
        int[][] result = new int[rowSize][colSize];
        for (int i = 0; i != result.length; i++) {
            for (int j = 0; j != result[0].length; j++) {
                result[i][j] = (int) (Math.random() * 10);
            }
        }
        return result;
    }

    //课堂上的代码
    public static int walk(int[][] matrix, int i, int j) {
        int x = matrix.length - 1;
        int y = matrix[0].length - 1;
        if (i == x && j == y) {
            return matrix[i][j];
        }
        if (i == x)//如果i到达行底部，只能向右走。
            return matrix[i][j] + walk(matrix, i, j + 1);

        if (j == y)//如果j到达列边界，只能向下走。
            return matrix[i][j] + walk(matrix, i + 1, j);
        //其他情况，需要对向下和向右进行对比，选出最优解
        int right = walk(matrix, i, j + 1);
        int down = walk(matrix, i + 1, j);
        return matrix[i][j] + Math.min(right, down);

    }


    public static void main(String[] args) {
        int[][] m = {{1, 3, 5, 9}, {8, 1, 3, 4}, {5, 0, 6, 1}, {8, 8, 4, 0}};
        System.out.println(minPath1(m));
        System.out.println(minPath2(m));

        m = generateRandomMatrix(6, 7);
        System.out.println(minPath1(m));
        System.out.println(minPath2(m));
    }
}

题目八

给你一个数组arr，和一个整数aim。如果可以任意选择arr中的数字，能不能累加得到aim，返回true或者false

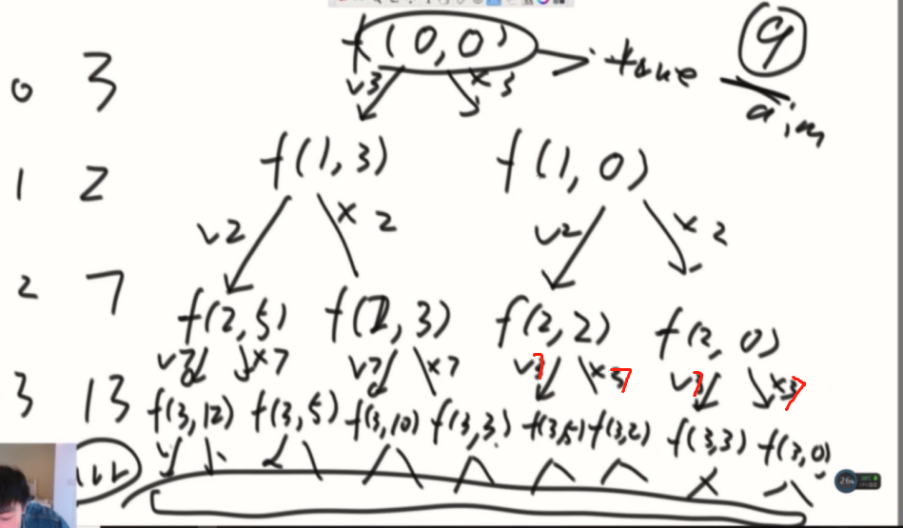
这是一个无后效性问题。可以使用dp，不管之前做了什么选择，只要是之前的累加和、步数是固定的，返回值一定确定。

i就是数组长度，sum的范围是全部数的和。

 

首先查看递归的base case，分析出最后一行，只有aim对应的列是T其余全是F，通过查看递归的规律，普遍的位置依赖的是两种情况，[i+1,sum]和[i+1,sum+arr[i]]，逐个计算把整个dp数组填满。如果aim超出sum，那肯定是计算不出来的，因为sum是数组全部数加起来的和。

最后计算出[0,0]的位置，可以直接返回。

和题意没关系了。（从暴力递归中总结出来）

有负数怎么办？要设计一下

 

public class Code_08_Money_Problem {

    public static boolean money1(int[] arr, int aim) {
        return process1(arr, 0, 0, aim);
    }

    public static boolean process1(int[] arr, int i, int sum, int aim) {
        if (sum == aim)
            return true;

        // sum != aim
        if (i == arr.length)
            return false;

        return process1(arr, i + 1, sum, aim) || process1(arr, i + 1, sum + arr[i], aim);
    }

    public static boolean money2(int[] arr, int aim) {
        boolean[][] dp = new boolean[arr.length + 1][aim + 1];
        for (int i = 0; i < dp.length; i++) {
            dp[i][aim] = true;//以目标金额为列的肯定为true
        }
        for (int i = arr.length - 1; i >= 0; i--) {//从最后一行开始
            for (int j = aim - 1; j >= 0; j--) {//aim往后的都超过，没必要看
                dp[i][j] = dp[i + 1][j];//通过直接的下方的判断。
                if (j + arr[i] <= aim) {//如果该数加上arr[i](当前可以累加的数)少于等于目标数。
                    // 有可能可行，通过查看加上了arr[i](当前可以累加的数)的状态来判断
                    dp[i][j] = dp[i][j] || dp[i + 1][j + arr[i]];
                }
            }
        }
        return dp[0][0];
    }

    public static boolean check(int[] arr,int i,int sum,int aim){
        if (i == arr.length){//判断是否走到最后一步
            return sum == aim;
        }
        return check(arr,i+1,sum,aim) || check(arr,i+1,sum+arr[i],aim);
    }



    public static void main(String[] args) {
        int[] arr = { 1, 4, 8 };
        int aim = 12;
//        System.out.println(money1(arr, aim));
//        System.out.println(money2(arr, aim));

        System.out.println(check(arr,0,0,aim));

    }

}

题目九

给定两个数组w和v，两个数组长度相等，w[i]表示第i件商品的重量，v[i]表示第i件商品的价值。 再给定一个整数bag，要求你挑选商品的重量加起来一定不能超过bag，返回满足这个条件下，你能获得的最大价值。

public class Code_09_Knapsack {

    public static int maxValue1(int[] c, int[] p, int bag) {
        return process1(c, p, 0, 0, bag);
    }

    public static int process1(int[] weights, int[] values, int i, int alreadyweight, int bag) {
        if (alreadyweight > bag) {
            return 0;
        }
        if (i == weights.length) {
            return 0;
        }
        //每次就两种情况：1、不拿商品 2、拿商品承担重量
        return Math.max(
                process1(weights, values, i + 1, alreadyweight, bag),
                values[i] + process1(weights, values, i + 1, alreadyweight + weights[i], bag));
    }
    //carat 克拉/重量  price 价值
    public static int maxValue2(int[] c, int[] p, int bag) {
        int[][] dp = new int[c.length + 1][bag + 1];
        for (int i = c.length - 1; i >= 0; i--) {
            for (int j = bag; j >= 0; j--) {//超过bag将毫无意义
                dp[i][j] = dp[i + 1][j];
                if (j + c[i] <= bag) {
                    dp[i][j] = Math.max(dp[i][j], p[i] + dp[i + 1][j + c[i]]);
                }
            }
        }
        return dp[0][0];
    }

    public static void main(String[] args) {
        int[] c = { 3, 2, 4, 7 };
        int[] p = { 5, 6, 3, 19 };
        int bag = 11;
        System.out.println(maxValue1(c, p, bag));
        System.out.println(maxValue2(c, p, bag));
    }

}