算法进阶面试题01——KMP算法详解、输出含两次原子串的最短串、判断T1是否包含T2子树、Manacher算法详解、使字符串成为最短回文串

1、KMP算法详解与应用

 

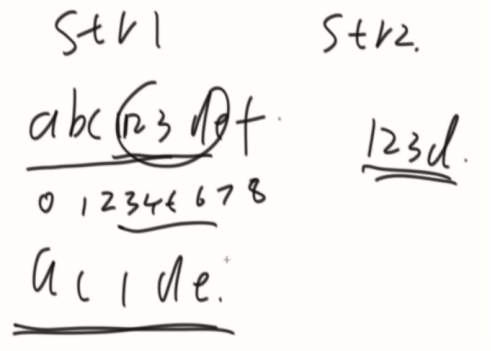
子序列：可以连续可以不连续。

子数组/串：要连续

 

暴力方法：逐个位置比对。

 

 

KMP：让前面的，指导后面。

概念建设：

d的最长前缀与最长后缀的匹配长度为3。（前缀不能到最后一个，后缀也不能到第一个）

 

 

先计算出str2的全部匹配信息。

 

 

一路相等，直到X与Y不匹配，根据X位置的最长前后缀信息加速。

 

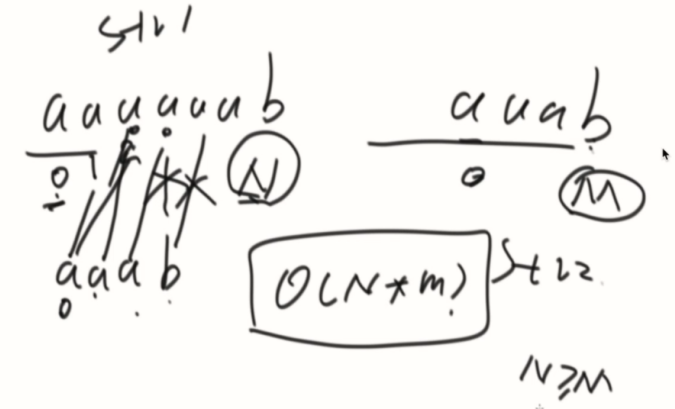
例子：

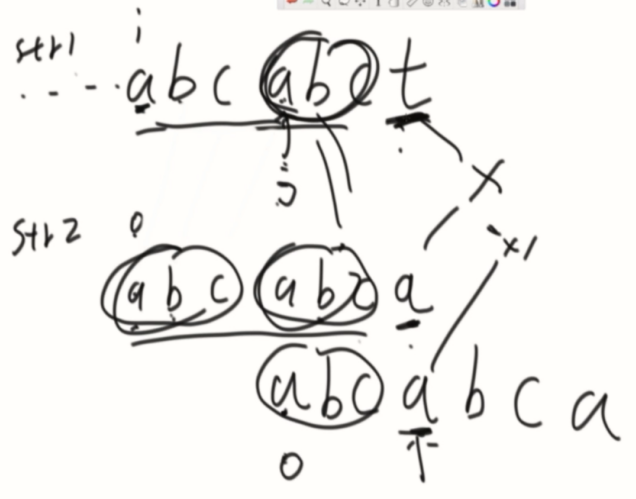
用str1的第一个不同的位置（t）从str2最长前缀的下标位置（a）开始比对。

 

（加强）再说说流程，举例子：

j是推到和后缀等量的位置，如果碰到一个字符最长前后缀为0（该位置没得加速），那么匹配字符就只挪动一位，再继续逐一比对。

 

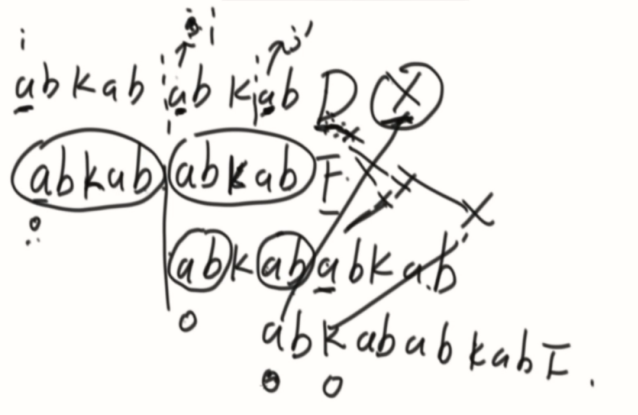
代码里面的实现：匹配到了甲乙位置，甲不动，乙根据Y最长前后缀的值去到前面。和甲继续比对。由于有等量的东西，所以就跳过了一部分值的比对。

 

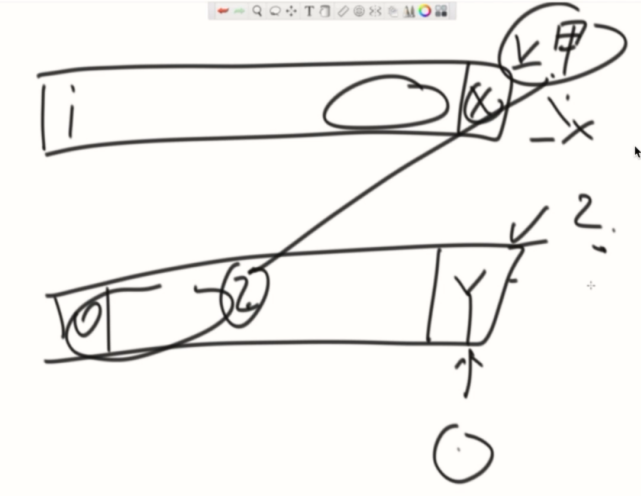
实质：

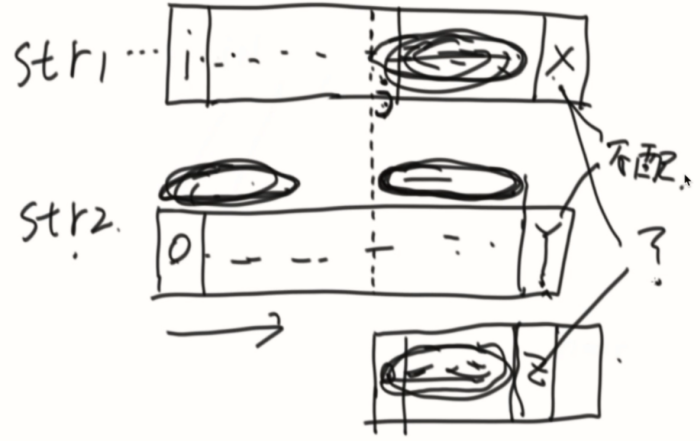
为什么i~j这些位置可以判断出，配不出str2？

 

假设可以从k出发配出全部str2，那么k~x应该和str2的前段等量相等（Y的前缀），k~x也对应着str2中的另一部分（Y的后缀），导致和之前找出的最长前后缀不一致，所以在之前的最长前后缀正确的情况下，是不可能的。

 

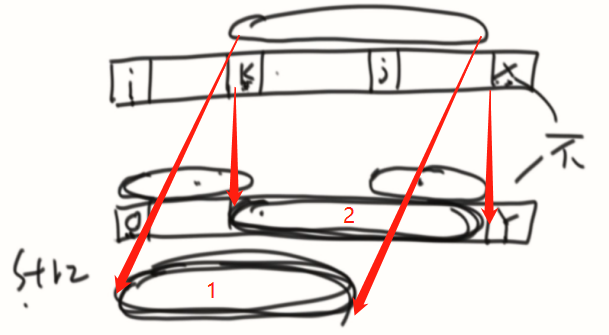
next数组怎么求？

数学归纳法，例如：a的位置，根据判断a的前一个b，和b的最长前缀后的一个是否相等来决定。

 

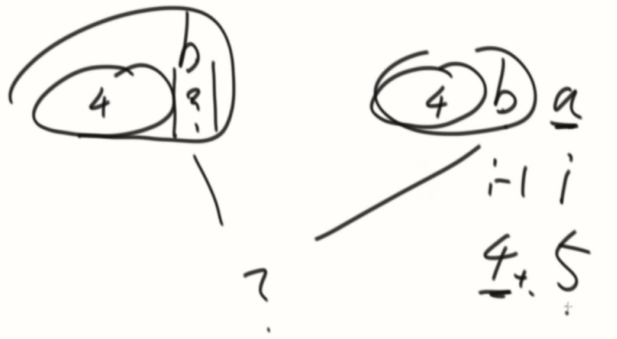
如果不等，就拿b最长前缀的下一个c的最长前缀的下一个来比对，一样就c的+1，不一样就继续拆分来看，一直到拆分不了才设置为0。

 

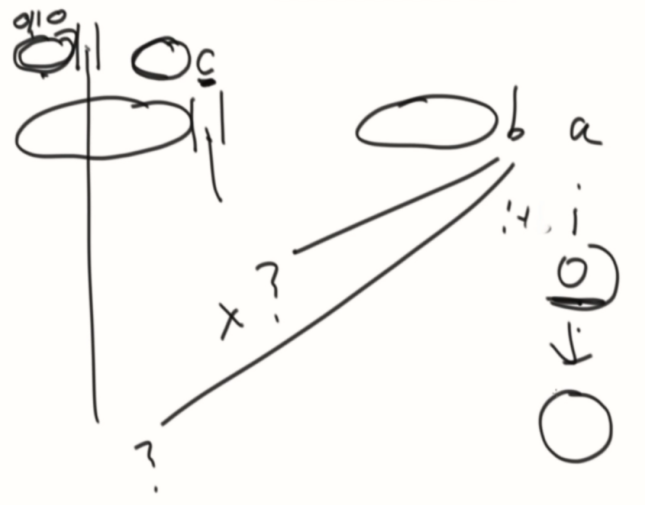
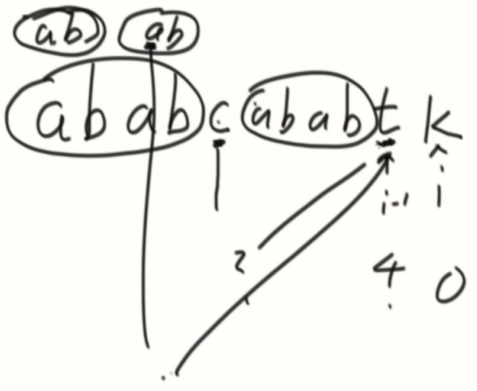
例子：

 

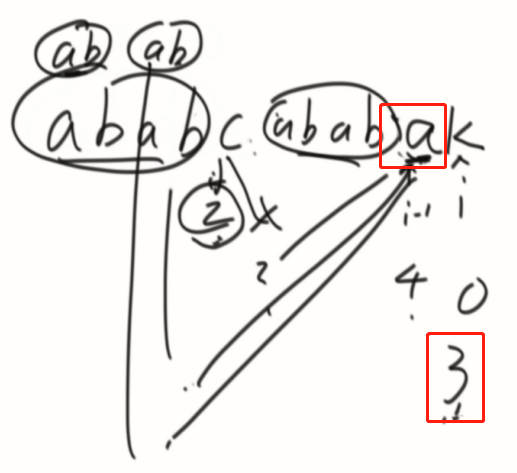
变换一下，把t变为a的情况：

 

分析代码....

public class Code_01_KMP {

    public static int getIndexOf(String s, String m) {
        if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {
            return -1;
        }
        char[] ss = s.toCharArray();
        char[] ms = m.toCharArray();
        //匹配下标
        int i1 = 0;
        int i2 = 0;
        int[] next = getNextArray(ms);
        while (i1 < ss.length && i2 < ms.length) {
            if (ss[i1] == ms[i2]) {
                i1++;
                i2++;
            } else if (next[i2] == -1) {//-1标志数组第一个字符
                i1++;//开头都配不上，就++
            } else {
                i2 = next[i2];//根据next的指引，往前跳，继续比对
            }
        }
        return i2 == ms.length ? i1 - i2 : -1;
    }

    public static int[] getNextArray(char[] str2) {
        if (str2.length == 1) {
            return new int[] { -1 };
        }
        int[] next = new int[str2.length];
        next[0] = -1;
        next[1] = 0;
        int pos = 2;
        int cn = 0;//跳到的位置
        while (pos < next.length) {
            if (str2[pos - 1] == str2[cn]) {
                next[pos++] = ++cn;
            } else if (cn > 0) {
                cn = next[cn];
            } else {
                next[pos++] = 0;
            }
        }
        return next;
    }

    public static void main(String[] args) {
        String str = "abcabcababaccc";
        String match = "ababa";
        System.out.println(getIndexOf(str, match));

    }

}

KMP应用。

2017秋招京东原题：

输出包含两次原子串的最短字符串

例如：

输入：aba

输出：ababa

 

计算输入字符的next数组，计算到最后一个位置，看看前面有多少是已经叠加复用的，不够再往后添加上字符。

 

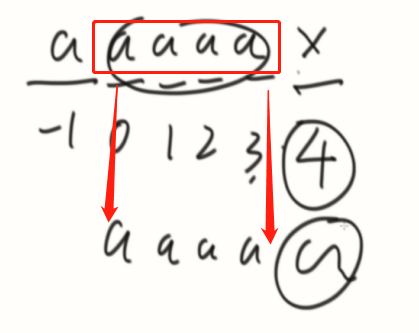
public class Code_02_KMP_ShortestHaveTwice {

    public static String answer(String str) {
        if (str == null || str.length() == 0) {
            return "";
        }
        char[] chas = str.toCharArray();
        if (chas.length == 1) {
            return str + str;
        }
        if (chas.length == 2) {
            return chas[0] == chas[1] ? (str + String.valueOf(chas[0])) : (str + str);
        }
        int endNext = endNextLength(chas);
        //该子字符串始于指定索引处的字符，一直到此字符串末尾。
        return str + str.substring(endNext);
    }

    public static int endNextLength(char[] chas) {
        int[] next = new int[chas.length + 1];
        next[0] = -1;
        next[1] = 0;
        int pos = 2;
        int cn = 0;
        while (pos < next.length) {
            if (chas[pos - 1] == chas[cn]) {
                next[pos++] = ++cn;
            } else if (cn > 0) {
                cn = next[cn];
            } else {
                next[pos++] = 0;
            }
        }
        return next[next.length - 1];
    }

    public static void main(String[] args) {
        String test1 = "a";
        System.out.println(answer(test1));

        String test2 = "aa";
        System.out.println(answer(test2));

        String test3 = "ab";
        System.out.println(answer(test3));

        String test4 = "abcdabcd";
        System.out.println(answer(test4));

        String test5 = "abracadabra";
        System.out.println(answer(test5));
    }

}

题目二：

在T1中找是否包含T2子树。

 

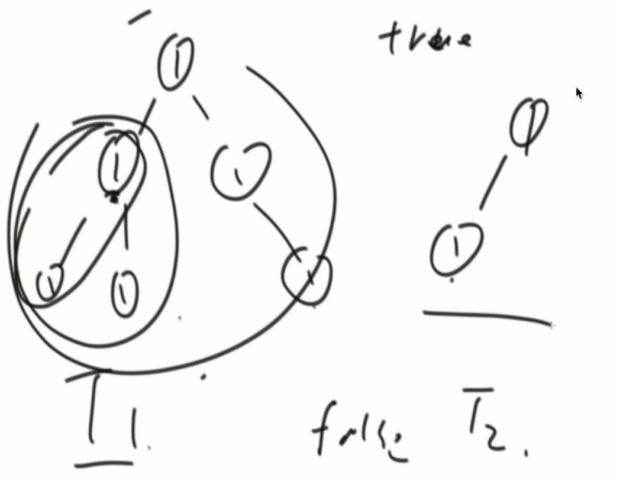
把T1和T2都序列化为串，判断是否为子串。

 

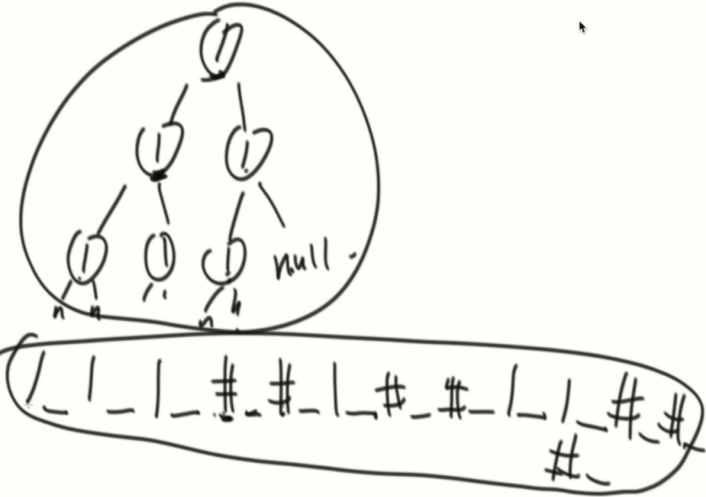
public class Code_03_KMP_T1SubtreeEqualsT2 {

    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }

    public static boolean isSubtree(Node t1, Node t2) {
        String t1Str = serialByPre(t1);
        String t2Str = serialByPre(t2);
        return getIndexOf(t1Str, t2Str) != -1;
    }

    public static String serialByPre(Node head) {
        if (head == null) {
            return "#!";
        }
        String res = head.value + "!";
        res += serialByPre(head.left);
        res += serialByPre(head.right);
        return res;
    }

    // KMP
    public static int getIndexOf(String s, String m) {
        if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {
            return -1;
        }
        char[] ss = s.toCharArray();
        char[] ms = m.toCharArray();
        int[] nextArr = getNextArray(ms);
        int index = 0;
        int mi = 0;
        while (index < ss.length && mi < ms.length) {
            if (ss[index] == ms[mi]) {
                index++;
                mi++;
            } else if (nextArr[mi] == -1) {
                index++;
            } else {
                mi = nextArr[mi];
            }
        }
        return mi == ms.length ? index - mi : -1;
    }

    public static int[] getNextArray(char[] ms) {
        if (ms.length == 1) {
            return new int[] { -1 };
        }
        int[] nextArr = new int[ms.length];
        nextArr[0] = -1;
        nextArr[1] = 0;
        int pos = 2;
        int cn = 0;
        while (pos < nextArr.length) {
            if (ms[pos - 1] == ms[cn]) {
                nextArr[pos++] = ++cn;
            } else if (cn > 0) {
                cn = nextArr[cn];
            } else {
                nextArr[pos++] = 0;
            }
        }
        return nextArr;
    }

    public static void main(String[] args) {
        Node t1 = new Node(1);
        t1.left = new Node(2);
        t1.right = new Node(3);
        t1.left.left = new Node(4);
        t1.left.right = new Node(5);
        t1.right.left = new Node(6);
        t1.right.right = new Node(7);
        t1.left.left.right = new Node(8);
        t1.left.right.left = new Node(9);

        Node t2 = new Node(2);
        t2.left = new Node(4);
        t2.left.right = new Node(8);
        t2.right = new Node(5);
        t2.right.left = new Node(9);

        System.out.println(isSubtree(t1, t2));

    }

}

题目三：

怎么判断一个字符串，不是由一个子字符串得到的。

123123123123、aabaabaabaabaab

KMP的应用，最后的结束位的前缀和后缀，会呈整数倍的关系。每次划分位置都是相等的整数倍。

 

KMP要好好消化。

 

二、Manacher算法详解与应用

最长回文子串。

暴力方式：o(n²)

全部加上#后，逐个计算回文（通过从当前字符每次比对临近左右两个数来计算），取出最大的回文数再除以2即答案。

 

 概念建设：

1、回文半径数组（存放每个位置对应的回文半径）

2、回文最右边界。（实际字符串有虚轴#）

 

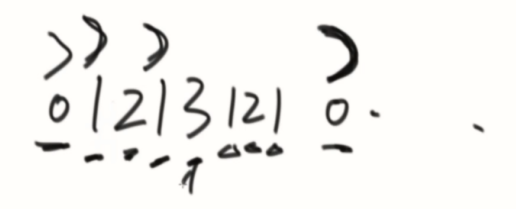
3、回文最右边界的中心

 

可能性：

1、不在最右边界里面，暴力扩充就行。

　   2、3、4是i在右边界里面的情况扩充。

2、i的回文半径在右边界里面。

 

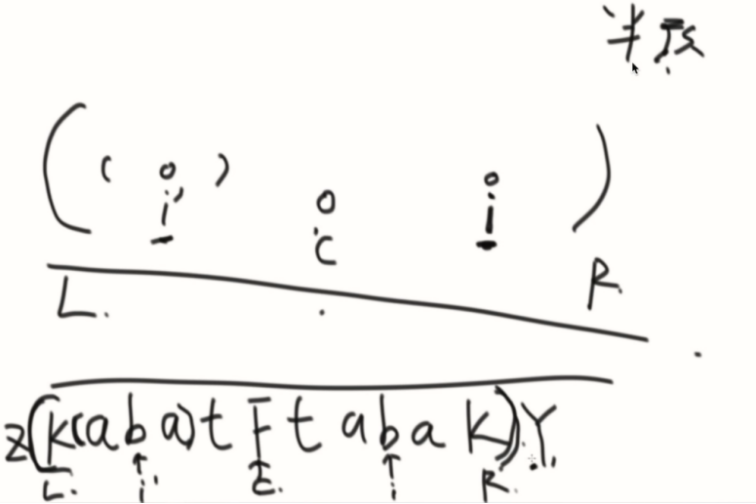
这种情况i不用计算，直接和i’一样。

证明：

 

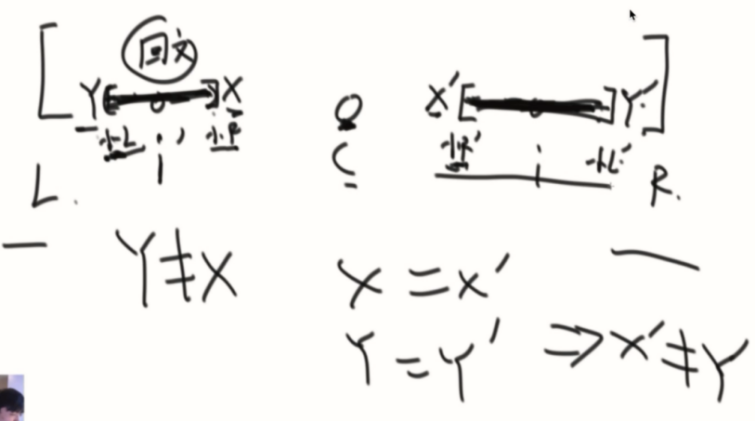
3、左边界没扩住i’的情况。i的回文半径是i~R

 

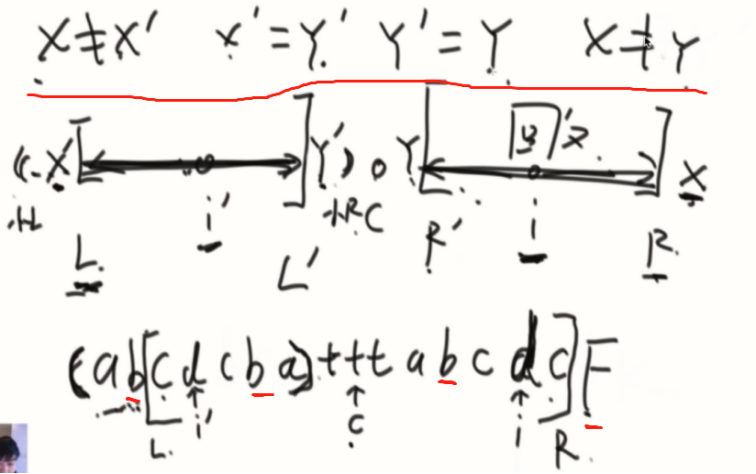
4、与L压线

从i~R是不用验证的，过了R之后还是要继续扩充验证。

 

 

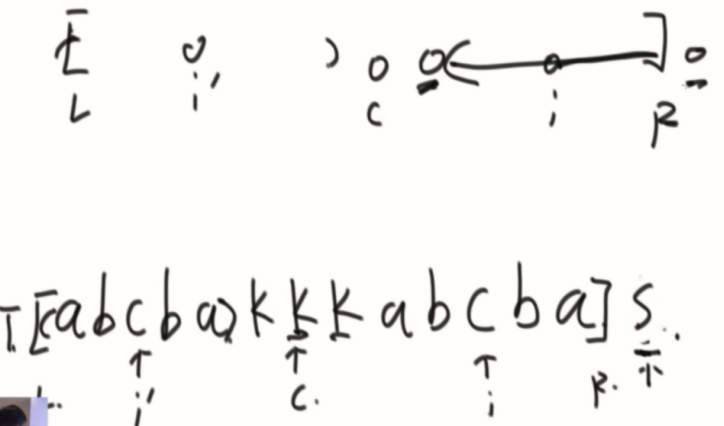
复杂度

 

 

再画一下各种情况

i在R内部。

①在内，直接等于i’的

 

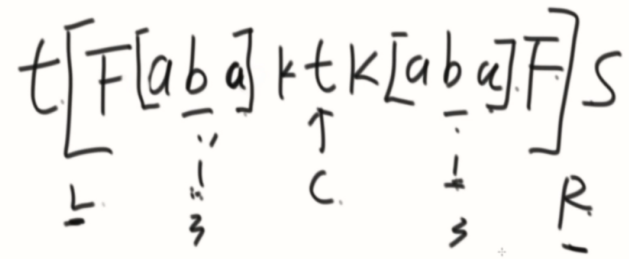
②L外，i~R

 

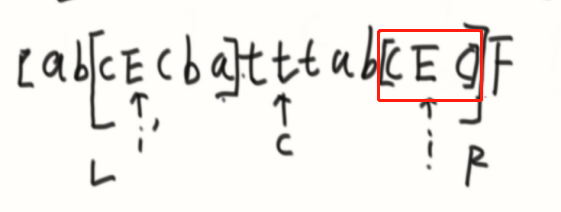
③压线，要继续向外扩充判断。

 

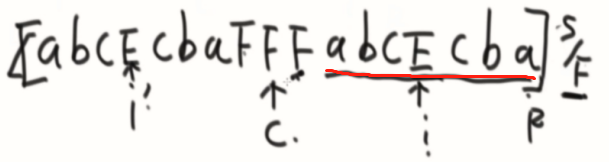
public class Code_04_Manacher {

    public static char[] manacherString(String str) {
        char[] charArr = str.toCharArray();
        char[] res = new char[str.length() * 2 + 1];
        int index = 0;
        for (int i = 0; i != res.length; i++) {
            res[i] = (i & 1) == 0 ? '#' : charArr[index++];
        }
        return res;
    }

    public static int maxLcpsLength(String str) {
        if (str == null || str.length() == 0) {
            return 0;
        }
        char[] charArr = manacherString(str);
        //回文半径数组
        int[] pArr = new int[charArr.length];
        int C = -1;
        int R = -1;
        int max = Integer.MIN_VALUE;
        for (int i = 0; i != charArr.length; i++) {
            //i'的回文和i~R的距离，谁更近就是i的瓶颈
            //2 * C - i --> i'的位置
            //pArr[2 * C - i]  i'的回文半径
            //R - i --> i到R的距离
            //R > i i在R的边界里面
            pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;
            //全部情况都往外扩，虽然情况2、3扩充一次后会直接失败，但统一简化了代码
            //检查是否越界
            while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {
                if (charArr[i + pArr[i]] == charArr[i - pArr[i]])
                    pArr[i]++;
                else {
                    break;
                }
            }
            //如果扩充区域超过了R，做相应的更新
            if (i + pArr[i] > R) {
                R = i + pArr[i];
                C = i;
            }
            //记录全局最大值
            max = Math.max(max, pArr[i]);
        }
        return max - 1;
    }

    public static void main(String[] args) {
        String str1 = "abc1234321ab";
        System.out.println(maxLcpsLength(str1));
    }

}

应用：如果只能在字符串最后添加字符，怎么让字符成为回文字符串？要求添加字符最少。

 

思路：就是在求必须包含最后一个字符串的情况下，最长回文串是多少，前面不是的部分逆序过来添上去。

 

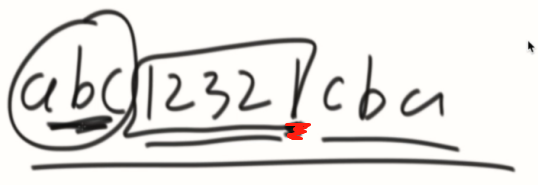
改写Manacher：

获得第一个达到最后边界的位置，知道了LR边界，把L边界前面的逆序，添加到总体字符串的后面，既是答案。

 

例子：

 

 

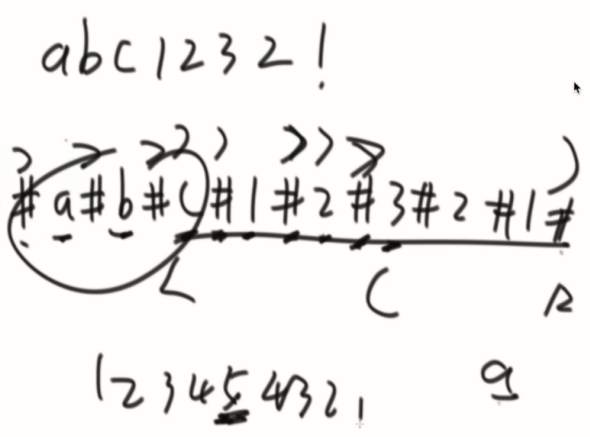
加#解决偶回文的问题

 

public class Code_05_Manacher_ShortestEnd {

    public static char[] manacherString(String str) {
        char[] charArr = str.toCharArray();
        char[] res = new char[str.length() * 2 + 1];
        int index = 0;
        for (int i = 0; i != res.length; i++) {
            res[i] = (i & 1) == 0 ? '#' : charArr[index++];
        }
        return res;
    }

    public static String shortestEnd(String str) {
        if (str == null || str.length() == 0) {
            return null;
        }
        char[] charArr = manacherString(str);
        int[] pArr = new int[charArr.length];
        int index = -1;
        int pR = -1;
        int maxContainsEnd = -1;
        for (int i = 0; i != charArr.length; i++) {
            pArr[i] = pR > i ? Math.min(pArr[2 * index - i], pR - i) : 1;
            while (i + pArr[i] < charArr.length && i - pArr[i] > -1) {
                if (charArr[i + pArr[i]] == charArr[i - pArr[i]])
                    pArr[i]++;
                else {
                    break;
                }
            }
            if (i + pArr[i] > pR) {
                pR = i + pArr[i];
                index = i;
            }
            if (pR == charArr.length) {
                maxContainsEnd = pArr[i];
                break;
            }
        }
        //原串 - 回文串 + 1 = 后补的长度
        char[] res = new char[str.length() - maxContainsEnd + 1];
        for (int i = 0; i < res.length; i++) {
            res[res.length - 1 - i] = charArr[i * 2 + 1];
        }
        return String.valueOf(res);
    }

    public static void main(String[] args) {
        String str2 = "abcd123321";
        System.out.println(shortestEnd(str2));

    }

}

要多练练，算法相伴随的衍生题目，提高敏感度。

 

代码解读：

取最近距离。

 

I’在区域内的情况：

 

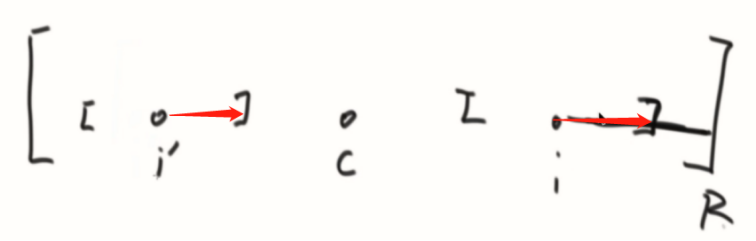
I’在区域外的情况：