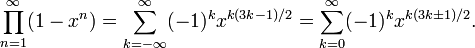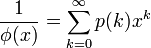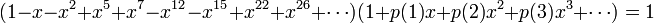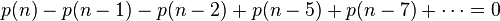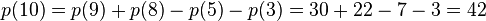2013 Multi-University Training Contest 5 Partition

思路：五边形数定理！！！

五边形数定理是一个由欧拉发现的数学定理，描述欧拉函数展开式的特性。欧拉函数的展开式如下：

亦即

欧拉函数展开后，有些次方项被消去，只留下次方项为1, 2, 5, 7, 12, ...的项次，留下来的次方恰为广义五边形数。

若将上式视为幂级数，其收敛半径为1，不过若只是当作形式幂级数（formal power series）来考虑，就不会考虑其收敛半径。

欧拉函数的倒数是分割函数的母函数，亦即：

其中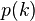为k的分割函数。

上式配合五边形数定理，可以得到

考虑项的系数，在 n>0 时，等式右侧的系数均为0，比较等式二侧的系数，可得

因此可得到分割函数p(n)的递归式

以n=10为例

这就是所求的了，当n<0时，p(n)=0;

p(n)的其他性质：

当限定将表示成刚好个正整数之和时，可以表示为。显然，。

• 对于，
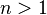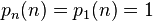
• (OEIS:A004526)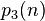
• = 最接近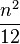的正整数。(OEIS:A069905)
• 
• 

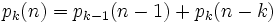
代码如下：

 

#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<iomanip>
#include<cmath>
#include<string>
#include<vector>
#define ll __int64
#define pi acos(-1.0)
#define MAX 100001
using namespace std;
const int mod=1000000007;
int an[MAX],n,t;
void init(){
    int i,j;
    an[0]=an[1]=1;
    an[2]=2;an[3]=3;an[4]=5;
    an[5]=7;
    for(i=6;i<MAX;i++){
        an[i]=0;
        for(j=1;;j++){
            int g=j*(3*j-1)/2;
            if(i-g<0) break;
            if(j&1) an[i]+=an[i-g];
            else an[i]-=an[i-g];
            an[i]=an[i]%mod;
            while(an[i]<0) an[i]+=mod;
            g=j*(3*j+1)/2;
            if(i-g<0) break;
            if(j&1) an[i]+=an[i-g];
            else an[i]-=an[i-g];
            an[i]=an[i]%mod;
            while(an[i]<0) an[i]+=mod;
        }
        an[i]%=mod;
    }
}
int main(){
    init();
    scanf("%d",&t);
    while(t--){
        scanf("%d",&n);
        printf("%d
",an[n]);
    }
    return 0;
}