五、过程式编程和调试技巧 返回目录页
1、循环
2、判断
3、模块化
4、循环+判断
5、调试技巧
MMA支持所有标准的过程式编程(Procedural programming)结构,但往往通过集成把它们扩展到更为普遍的符号编程环境中。
-------------------------------------------------------------------------
1、循环
MMA支持多种循环,常用的是Do循环与While循环。
----------------------------------------
特殊形式的赋值
i++ i 加 1
i-- i 减 1
++i 先给 i 加 1
--i 先给 i 减 1
i+=di i 加 di
i-=di i 减 di
x*=c x 乘以 c
x/=c x 除以 c
x=y=value 对 x 和 y 赋同一值
{x,y}={value,value} 对 x 和 y 赋不同的值
{x,y}={y,x} 交换 x 和 y 的值
----------------------------------------
迭代器。
没啥新鲜的,以前在用Table函数时,就已经用到过。
最后一行指控制多重循环。
----------------------------------------
语句块
因为在MMA中,只有表达式(唯一的例外是序列,但序列不能单独使用),所以语句块,也是表达式块。
语句块的作用,是将多个语句组合起来,而形成一个语句(表达式)。
在MMA中,没有专用的语句块符号,如Pascal语言中的Begin/End,如C语言中的{}。
如果实在要用,就用()。而且有时候是必须的,而有时候又不是必须的。
test[n_, i_] := (t = 2^n; Plus[t, i])
test[2, 2]
前一行中,()是必须的。()内两个语句,第一句运行没输出。第二句运行也没输出,但计算结果作为函数的返回值返回了——从而在函数被调用的时候,产生输出。
Do[
(Print[a];
Print[b];
Print[c];
Print[d]),
{1}]
这个()是多余的,不是必须。用上与没用上效果一样。
但用上了之后,代码的可读性似乎增加了。
语句块是支持嵌套的:
(((a; b; c); (d; e)); (f; g))
但不常用,基本上见不到这种用法。(倒是让人想到了Lisp语言家族的表达式)
----------------------------------------
Do 循环。
Do循环的构成非常简洁:
Do[expr,迭代器]
Do[Print[你好], {2}]
Table[你好, {2}]
在语法上,Do函数与Table很像。Table函数创造出表,Do函数运行表达式数次。
expr部分,可以是单条语句,也可以是语句块。
Do[Print[你好吗]; Print[很好], {2}]
这个语句块中的()不是必须,但如果用上也行。
Do[(Print[你好吗]; Print[很好]), {2}]
因为步长可以是负值,实现“Down to”就很容易。
Do[Print[i], {i, 10, 8, -1}]
迭代器实际上是很灵活的,不一定用整数,可以用符号值。
Do[Print[n], {n, x, x + 3 y, y}]
实际多重循环,也是易如反掌:
Do[Print[{i, j}], {i, 3}, {j, i - 1}]
在MMA中,循环又叫迭代。
t = x; Do[t = 1/(1 + t), {5}]; t
Nest[1/(1 + #) &, x, 5]
这两行语句的效果是一样的。
Do[Print[RandomInteger[{1, 30}]], {10}]
输出10个1到30之内的伪随机数。
其实有内置函数来做这事:
RandomSample[Range[30], 20]
内置函数不熟悉的话,就是比较吃亏。
要注意的一点是,Do函数本身没有返回值(即返回Null)。
Null
是一个符号,用来指明一个表达式或结果不存在。 在普通输出中它不显示。
当 Null 显示为一个完全输出表达式时,没有任何输出显示。
Null
得:无输出。
所以为了观察循环体内的运算过程,我们用了很多Print输出。
----------------------------------------
While 循环。
基本格式也极其简洁:
While[test,body]
重复计算 test,然后是 body,直到 test 第一次不能给出 True。
body部分,可以是单条语句,也可以是语句块。语句块用不用(),均可。
n = 1; While[n < 3, Print[n]; n++; Print[hello]]
n = 1; While[n < 3, (Print[n]; n++; Print[hello];)]
最后一个分号,写不写上均可。
n = 1; While[n < 4, Print[n]; n++]
写成以下这样,效果都一样:
n = 1; While[n < 4, (Print[n]; n++;)]
n = 1; While[n < 4, n++; Print[n - 1];]
n = 1; While[n++ < 4, Print[n - 1]]
{a, b} = {27, 6};
While[b != 0, {a, b} = {b, Mod[a, b]}];
a
辗转相除法求最大公约数。
类似的方法,可以求出一系列的Fib数。
{a, b} = {0, 1}; n = 0;
While[n++ < 10, {a, b} = {b, a + b}; Print[b]]
Break 退出 While:
{a, b} = {0, 1}; n = 0;
While[True, n++; If[n > 10, Break[]]; {a, b} = {b, a + b}; Print[b]]
While 返回的最后结果是 Null。
-------------------------------------------------------------------------
2、判断
判断指一些条件函数(conditional function),依据条件(condition)的不同返回值(True/False/不确定)而返回不同表达式的值。
----------------------------------------
IF 判断。
If[condition,t]
如果 condition 计算为 True 给出 t,如果它计算为 False,则给出 Null。
If[condition,t,f]
如果 condition 计算为 True 给出 t,如果它计算为 False 给出 f。
If[condition,t,f,u]
如果 condition 计算既不为 True 也不为 False 给出 u。
奇怪哈,居然条件计算结果有第三种可能?
这就是符号计算的特色了。看:
a =.; b =.;
If[a == b, t, f, u]
得u
因为a、b只是符号,还不知道是啥值,所以a与b是不是相等?不知道。
condition部分,可以是语句块。()不是必须。
If[(a = 1; b = 2; a == b), t, f, u]
If[a = 1; b = 2; a == b, t, f, u]
分号、逗号一大堆,加上清楚好多。
当然,顺理成章,t/f/u部分,都可以是语句块。
a =.; b =.;
If[a == b, t, f]
得:If[a == b, t, f]
如果 condition 计算既不为 True 也不为 False,If[condition,t,f] 保持不计算。
abs[x_] := If[x < 0, -x, x]
abs /@ {-1, 0, 1}
If[TrueQ[2 < 4], 1, 0]
得:1
If[TrueQ[2 < 1], 1]
得:Null(无输出)
If支持嵌套。
如果x为1,得a,x为2,得b,x为3,得c,x为其他,得other。用If嵌套这样写:
x = 20;
If[x == 1, a,
If[x == 2, b,
If[x == 3, c, other]]]
其实这样写也可以。但用以下函数Which更好。
----------------------------------------
Which
看程序就很明白了。
x=2;
Which[x==1,a,x==2,b,x==3,c,True,other]
----------------------------------------
Switch
一样,看程序:
Switch[x, 1, a, 2, b, 3, c, _, other]
-------------------------------------------------------------------------
3、模块化
MMA一般假设变量是全局变量。即每次使用 x 等名字时,MMA总认为在调用同一对象。
然而在编程时,不需要将所有变量都作为全局变量。很多时候,我们希望用局部变量,比如在自定义函数体内。
在MMA中,可以用Module函数定义局部变量,可以用With函数定义局部常量。
----------------------------------------
Module
Module[{x,y,...},body] 具有局部变量 x,y,...的模块
t = 1;
Module[{t=t+2}, t=t+2; Print[t]];
t
这个程序很能说明问题了。
全局变量t,可以到Module的{}中去,而局部变量t是仅模块内可用的。
仔细观察可以看到,两个t的颜色是不同的。
如图,在“偏好设置”中,把三种变量设置成不同的颜色,是很重要的。
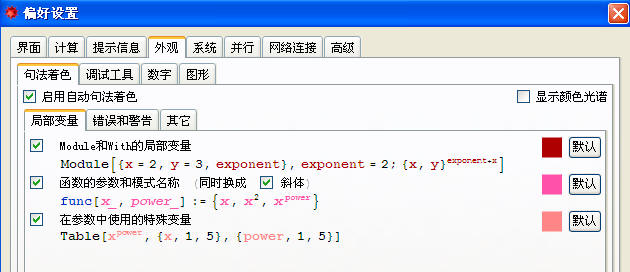
Module函数是有返回值的,即body表达式的返回值。
t = 1;
x = Module[{t = t + 2}, (t = t + 2; Print[t]; t + 2)];
t
x
body可以是语句块,这个语句块可以加上(),也可以不加。
----------------------------------------
With
在 Module 中可以定义局部变量,这样我们可以对其赋值并且改变其值。
然而,通常我们所需要的是局部常量,对其我们仅需要赋值一次。
With 结构可以建立局部常量。
With[{x=x0,y=y0...},body] 定义局部常量 x,y,...
这样是不可以的,因为局部常量不可以在body中再改变。
t = 1;
With[{t = t + 2}, t = t + 2; Print[t]];
t
这样就可以了:
t = 1;
With[{t = t + 2 + 2}, Print[t]];
t
可以将 With 理解为 /. 运算的推广:
t = 1;
t /. t -> t + 2 + 2
t
With 类似于局部变量仅赋值一次的 Module 的特殊形式。
With函数有返回值,即返回body表达式的输出值。
t = 1;
x = With[{t = t + 2 + 2}, Print[t]; t + 2];
t
x
还有个模块函数叫块(Block)。因为Block与Module有细微差别,这里不展开,有兴趣的小朋友可以研究帮助文档。
-------------------------------------------------------------------------
4、循环+判断
过程式编程,用循环+判断,可以解决很多问题。
如果要自定义函数,则要结合模块。
这里举几个栗子。
----------------------------------------
fib[n_] := Module[{f},
f[1] = f[2] = 1;
f[i_] := f[i] = f[i - 1] + f[i - 2];
f[n]
]
fib[5]
----------------------------------------
对最大公约数(GCD)使用初始化局部变量的欧几里德(Euclid)算法。
通常叫辗转相除法。
gcd[m0_, n0_] := Module[{m = m0, n = n0},
While[n != 0, {m, n} = {n, Mod[m, n]}];
m
]
gcd[120, 48]
----------------------------------------
筛法求素数。
primes2[n_] :=
Module[{primes = Range[n], p = 2},
Print["Start: primes = ", primes, ", p=", p];
While[p != n + 1, Do[primes[[i]] = 1, {i, 2 p, n, p}];
p = p + 1;
While[p != n + 1 && primes[[p]] == 1, p = p + 1];
Print["In loop: primes=", primes, ", p= ", p];];
Select[primes, (# != 1) &]]
primes2[12]
这个程序输出了中间过程,帮助理解筛法的思路。
以下程序加了中文注释,是不可以运行的,只能用于理解:
primes2[n_] :=
Module[{primes = Range[n], p = 2},
Print["Start: primes = ", primes, ", p=", p]; 输出初始表,及p值
While[p != n + 1,
Do[primes[[i]] = 1, {i, 2 p, n, p}]; 置1是在这里进行的,i从2p到n,步长为p
p = p + 1;
While[p != n + 1 && primes[[p]] == 1, p = p + 1]; 如果越界,或者p位置上已经是1,跳过,再p+1
Print["In loop: primes=", primes, ", p= ", p]; 输出循环时的表及p值
];
Select[primes, (# != 1) &]] 将置1的值从表中删除,剩下的就是素数
primes2[12]
把中间过程去掉:
primes[n_] :=
Module[{primes = Range[n], p = 2},
While[p != n + 1, Do[primes[[i]] = 1, {i, 2 p, n, p}];
p = p + 1;
While[p != n + 1 && primes[[p]] == 1, p = p + 1];];
Select[primes, (# != 1) &]]
primes[100]
这里有两个primes,名称相同,意义完全不同(一个是全局变量、另一个是局部变量)。在程序中,显示的颜色也不同。
如果用内置函数,一句就行:
Prime[Range[25]]
-------------------------------------------------------------------------
5、调试技巧
MMA中,有自带的调试器,菜单中:计算/调试,就可以打开调试器。这里不展开。
这里说一些小技巧。
A、如果发现莫名其妙的结果,多数是某个名称在前面被取绰号了,赶紧用Clear试试。
B、如果函数名记不全,有自动完成功能,很好用,可以先输入一两个字母(注意,大小写敏感的)。
C、多按F1,查帮助文档。MMA的帮助文档,可能是史上最强大的。
D、表达式的计算过程很难理解的时候,或者表达式很长的时候,用绰号来拆分。
E、用Trace函数来跟踪输出。
F、在程序中加入Abort函数来终止程序执行。加入到不同部分,可以分步调试。
G、很重要的一点是,用Print函数来输出中间结果,从而观察中间结果。输出中间结果是万精油,各种语言都可以通过此大法来调试。
H、长时间调试程序容易疲倦。疲倦时就休息,坚持下去经常效率并不高。
I、程序长时间运行,得不出结果,很可能进入死循环了,按 Alt+. 终止程序执行。
J、MMA是很庞大的系统,短时间内不精通不用心急。先掌握简单的。
K、越扯越远。。打住
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
23:44 2016-10-29
+++++++++++++++++++++++++++