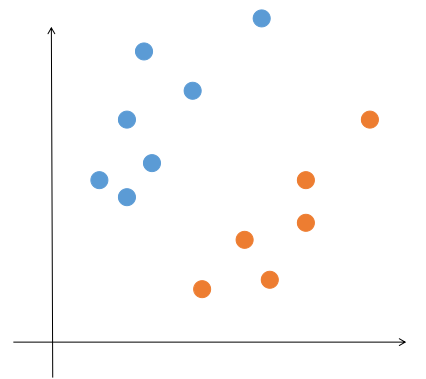
在上篇博客中提到,如果想要拟合一些空间中的点,可以用最小二乘法,最小二乘法其实是以样例点和理论值之间的误差最小作为目标。那么换个场景,如果有两类不同的点,而我们不想要拟合这些点,而是想找到一条直线把点区分开来,就像下图一样,那么我们应该怎么做呢?这个是一个最简单的分类问题。
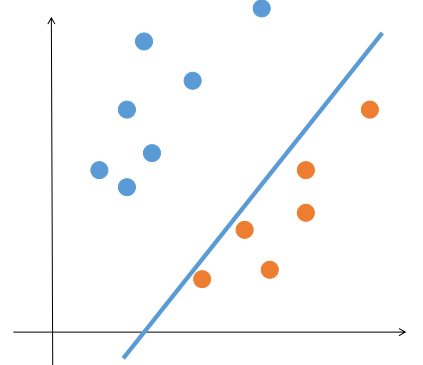
- 随机给定 w, b
- 找到当前这条直线 (ax_{1}+bx_{2}+c=0) 的情况下,找到所有分错的点(x_no,y_no)
- 把直线写作矩阵的形式:(wx+c=0),其中(w=(w_{1},w_{2})), (x=(x_{1},x_{2})^ mathrm{ T }),然后通过找到的误分点用梯度下降法进行参数调优。
(frac{partial L(w, b)}{partial w}=sum_{i=1}^{n} y_{i}x_{i})
(frac{partial L(w,b)}{partial b}=sum_{i=1}^{n} y_{i})
(w:=w+alpha*sum_{i=1}^{n} y_{i}x_{i})
(b:=b+alpha*sum_{i=1}^{n} y_{i})
其中 (alpha) 是学习率。 - 重复 2, 3 步。直到找不到错分的点或者到达迭代上限为止。
经过实验发现这种目标函数收敛比*方的那个的要快,而且对于点刚好在直线上时,*方法中求出来的 a, b 的梯度都是 0,就无法处理了,所以只能认为刚好在直线上也是分对了。而这种方法由于有 (y_{i}) 的先验知识,b 的梯度至少不会是0,可以处理这种情况。当然还可以用点到直线的距离来代替用来计数的函数:, 同样用 (y_{i}) 去绝对值,但是没有必要,徒增了很多复杂度。
如果初始值是线性不可分的,就会出现不收敛,一直在交叉的点之间震荡的情况。
这个就是传说中的感知机算法,这里的例子都是二维的,但是对于多维的情况也是一样的。无非就是直线变成一个超*面 $wx+b=0 ,x = (x0,x1,...,xn), w = (w0,w1,...,wn) $了。感知机算法本身还有很多内容,比如如何证明算法是收敛的,用对偶方法提高速度等等,这些跟主线无关~,以后再写吧。
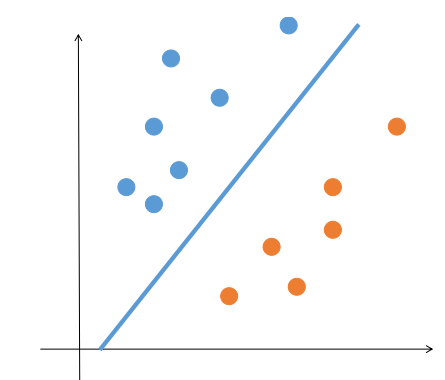
感知机算法虽然能够将线性可分的数据集区分开,但是比较没追求...只要能找到一条能把两类点完全分开的直线就满足了。但是这样的直线是有无穷多条的,我们希望能根据训练数据找到一条“最优”的,这样有利于算法的泛化能力,也更加充分的利用了数据的信息。比如下图:
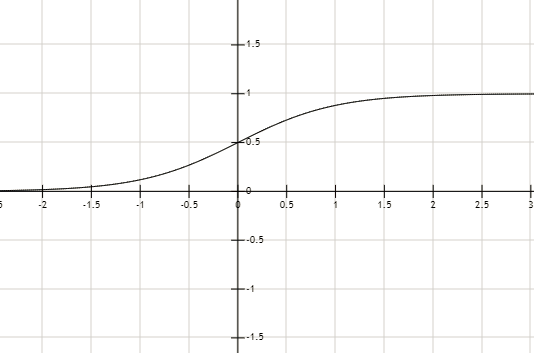
而感知机中用的是阶跃函数,相对比较粗糙。
其中用 sigmoid 函数作为激活函数的就算法就叫 logistic 回归了,也是最常用的。sigmod 函数在 x > 0 的时候 y > 0.5, x< 0 的时候 y<0.5。这样函数就能与 0.5 进行比较,从而自动识别出点是否分对,以及分对(或分错)的程度了。
那么这个怎么转化为需要最大化的目标函数呢?其实这个还是用直线进行划分,我们还是假设 {a, b} 两类,其中让 a 类带入直线大于 0, b 类小于零(之前已经解释,这样做是没有问题的) 那么对于某个点,如果它是 a 类,我们就让 p 尽量大 ,如果是 b 类我们是要让 1 - p 尽量大。把这个目标写成式子就是:对于某个点,我们要 ((y_{i} - a) p_{i} + (y_{i} - b) (1 - p_{i})) 尽量大。为了方便,我们就取 a、b 为 0, 1,式子就变成 $y_{i}p_{i} + (y_{i} - 1) (1 - p_{i}) $了。所以对于整个数据集目标就是最大化 (sum y_{i}p_{i} + (y_{i} - 1)(1-p_{i}))。可以对它直接求偏导进行参数优化。在最优化问题的,一般习惯上喜欢最小化某个函数,而那个函数就叫损失函数。所以这里可以把 (-sum y_{i}p_{i} + (y_{i} - 1)(1-p_{i}))作为损失函数,要让它最小。这样做是没问题的,但是比较朴素,效果也不好。
其实对于 sigmoid 函数而言,它已经把最后的输出值限制在 [0, 1] 的范围内,并且是以 0.5 为界。那么我们就可以把输出值看做一个概率,把分对、分错的程度(确信度)用一个概率值表示出来当分对的概率大于 0.5 的时候,我们就可以认为确实分对了。这样就有很多更好的损失函数的公式可以直接用进来,比如交叉熵,极大似然估计等。
比如用交叉熵,交叉熵的公式是:(H(p,q)=-sum_{x} p(x)logq(x)),其中p(x)表示训练样本的标签,q(x) 表示模型预测的值,它其实是衡量了预测的值的分布和真实标签分布之间的距离,具体参看 wiki 百科。
这里带入交叉熵公式得到的损失函数是:$-sum_{i=1}^{n} y_{i}p(x_{i}) + (y_{i} - 1)(1-p(x_{i})) $ 其中 n 为训练样本数。用的时候一般需要对 n 做个归一化,得到$-frac{1}{n}sum_{i=1}^{n} y_{i}p(x_{i}) + (y_{i} - 1)(1-p(x_{i})) $ 。
然后用梯度下降法优化就行了,步骤是:
- 获取 n 个训练样本 (x_{1}, x_{2}, y) , y 属于({0,1})
- 对于直线 (wx+b=0),需要 $min L(w, b) = -frac{1}{n}sum_{i=1}^{n} y_{i} sigmoid(x_{i}))) + (y_{i} - 1)(1-sigmoid(x_{i}))) (,对参数求梯度: )frac{partial L(w,b)}{w}=-frac{1}{n}sum_{i=1}^{n} x_{i}(y_{i}-sigmoid(wx_{i}+b))( )frac{partial L(w,b)}{b}=-frac{1}{n}sum_{i=1}^{n} y_{i}-sigmoid(wx_{i}+b)( )w := w - alpha frac{partial L(w,b)}{w}( )b := b - alpha frac{partial L(w,b)}{b}$
- 重复 1,2,直到 w, b 的梯度小于某个很小的值,或者达到循环上限。
如果用极大似然估计,由于在极大似然估计中需要取对数操作,为了方便,可以把 (y_{i} p + (1 - y_{i}) (1-p)) 改写为 (p^{y_{i}} (1-p)^{1 - y_{i}}),这两个是完全等价的。极大似然估计写出来的式子是:
然后为了计算方便,取对数。为了把这个 max 变成 min,需要进行取反,这都是极大似然估计的标准步骤:
最后发现两种方法得到的表达式是一样的,所以后面的优化步骤都一样。
这个就是 logistic 回归的思路了。这里还是用二维的举例,对于高维的情况几乎是一样的,就是参数从 ((w_{1},w_{2}))变为 ((w_{1},w_{2},...,w_{n}))了而已。由于 logistic 回归是基于全部点去定义、优化目标函数,所以已经解决了只能处理二分类的问题。logistic 回归可以很容易的扩展成能多分类的 softmax 算法,softmax 算法对于 n 类,就用 n-1 个超*面把它们分开。这个就是另外一个方法了。
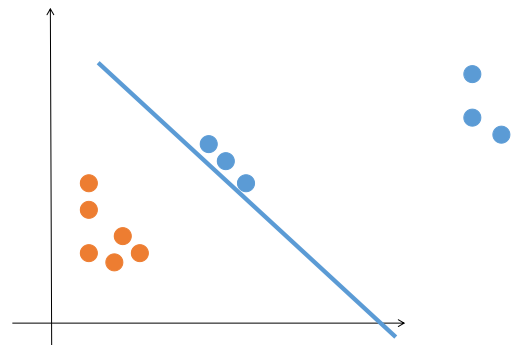
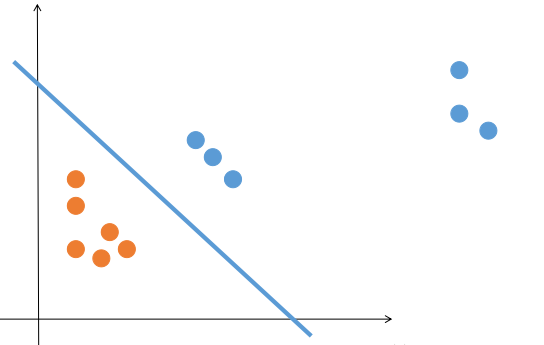
那么 logistic 回归就是完美的了吗,它至少还有两个缺点:1. 还是只能解决数据线性可分的问题 2. 考虑所有的点得到的最优直线还是会带来一些问题,比如:

参考链接:
如需转载,请注明出处.
出处:http://www.cnblogs.com/xinchen1111/p/8762186.html