介绍:
数据:就是21世纪的石油,而数据分析就是可以让我们发挥这些信息功能的重要手段。
数据分析可以做什么?
例子:
1.淘宝可以观察用户的购买记录,搜索记录以及人们在社交媒体上发布的内容选择商品推荐。
2.股票可以根据相应的数据选择买进卖出
3.今日头条可以将数据分析应用到新闻推送排行算法当中
4.爱奇艺可以为用户提供个性化电影推荐服务
为什么用python进行数据分析
1.python的代码语法简单易学
2.python可以很容易的整合C、C++等语言的代码
3.python有大量用于科学计算的库
4.python不仅可以用于研究和原型构建,同时也适用于构建生产系统
Ipython:
安装:pip install ipython
jupyter notebook
安装和启动有两种方式
一:命令行安装:
pip install jupyter
启动:
C:Usersoldboy>jupyter notebook
缺点:
必须手动安装数据分析包
二:anaconda
Anaconda是Python的一个开源的发行版本,里面包含了很多科学计算相关的包,它和Python的关系就像linux系统中centos和Ubuntu的关系一样,不冲突,你可以同时在电脑上安装这两个东西。那至于为什么我已经在电脑上安装了pycharm还要安装这个Anaconda呢,主要有以下几点原因: (1)Anaconda附带了一大批常用数据科学包,它附带了conda、Python和 150 多个科学包及其依赖项。因此你可以用Anaconda立即开始处理数据。 (2)管理包。Anaconda 是在 conda(一个包管理器和环境管理器)上发展出来的。在数据分析中,你会用到很多第三方的包,而conda(包管理器)可以很好的帮助你在计算机上安装和管理这些包,包括安装、卸载和更新包。 (3)管理环境。为什么需要管理环境呢?比如你在A项目中用到了Python2,而新的项目要求使用Python3,而同时安装两个Python版本可能会造成许多混乱和错误。这时候conda就可以帮助你为不同的项目建立不同的运行环境。还有很多项目使用的包版本不同,比如不同的pandas版本,不可能同时安装两个pandas版本。你要做的应该是在项目对应的环境中创建对应的pandas版本。这时候conda就可以帮你做到。 总结:Anaconda解决了官方Python的两大痛点: (1)提供了包管理功能,Windows平台安装第三方包经常失败的场景得以解决 (2)提供环境管理功能,解决了多版本Python并存、切换的问题。
下载:https://www.anaconda.com/distribution/#download-section

按照上面的路径点击下载,下载完成后就可以一路点击下一步完成安装,如果中间需要修改安装路径可以自己改一下。安装成功之后我们会发现,多出来几个应用
- Anaconda Navigtor :用于管理工具包和环境的图形用户界面,后续涉及的众多管理命令也可以在 Navigator 中手工实现。
- Jupyter notebook :基于web的交互式计算环境,可以编辑易于人们阅读的文档,用于展示数据分析的过程。
- qtconsole :一个可执行 IPython 的仿终端图形界面程序,相比 Python Shell 界面,qtconsole 可以直接显示代码生成的图形,实现多行代码输入执行,以及内置许多有用的功能和函数。
- spyder :一个使用Python语言、跨平台的、科学运算集成开发环境
配置环境变量
windows环境需要在控制面板系统和安全系统高级系统设置环境变量用户变量PATH当中添加anaconda的安装目录的Scripts文件夹。
验证:
打开命令行输入conda --version,如果能输出版本号就对了
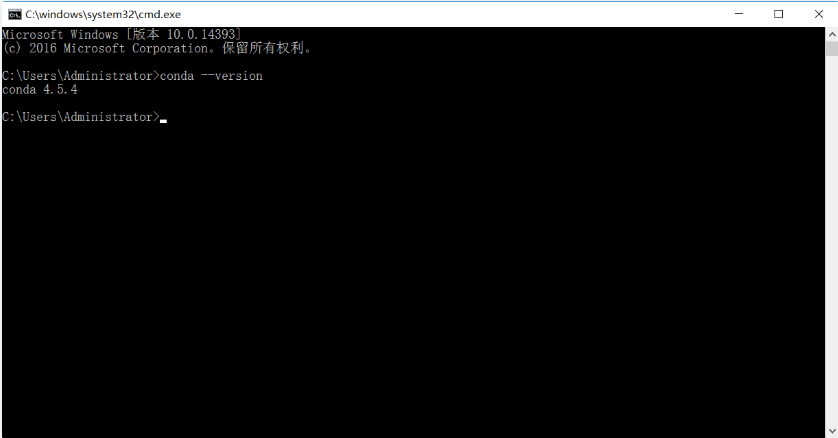
运行Anaconda
打开安装的Anaconda文件
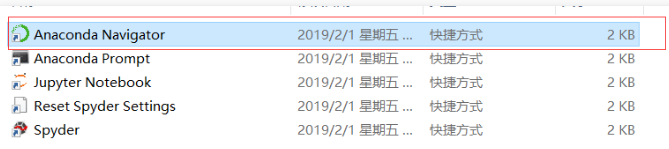
点击Anaconda Navigator运行
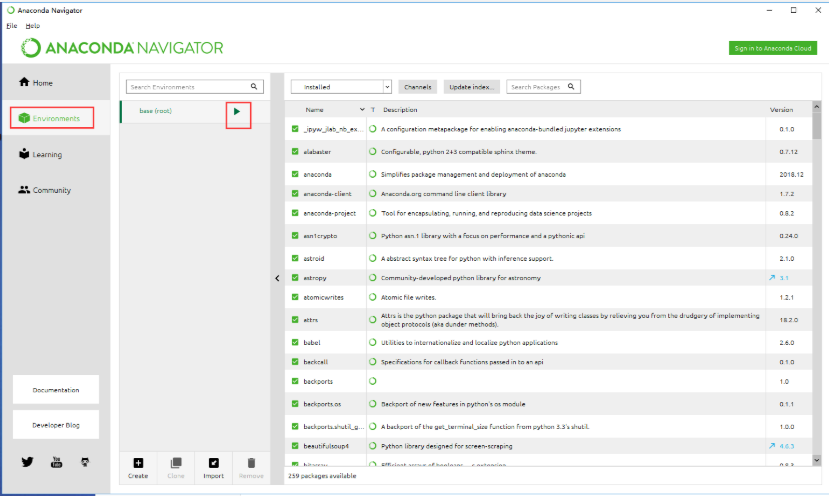
选择图中圈起来的按钮,会弹出来四个选择,选择最后一个Jupyter Notebook就可以打开代码编辑工具,如果不是用谷歌浏览器打开的,先尝试修改默认浏览器,或者按照第七条的补充内容进行修改
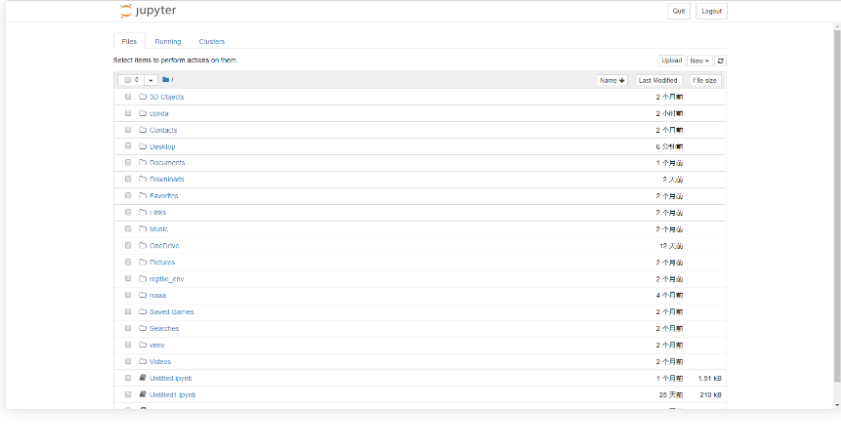
以上就是我们本机的根目录,就类似于windows系统的User目录,接下来就可以点击右上角的New按钮选择创建一个Python3文件,这个文件的后缀名是.ipynd.
接下来我们所有的程序都要在这个上面进行编写:
Numpy的用法
简介
Numpy是高性能科学计算和数据分析的基础包。它也是pandas等其他数据分析的工具的基础,基本所有数据分析的包都用过它。NumPy为Python带来了真正的多维数组功能,并且提供了丰富的函数库处理这些数组。它将常用的数学函数都支持向量化运算,使得这些数学函数能够直接对数组进行操作,将本来需要在Python级别进行的循环,放到C语言的运算中,明显地提高了程序的运算速度。
引用方法
import numpy as np
这是官方认证的导入方式,可能会有人说为什么不用from numpy import *,是因为在numpy当中有一些方法与Python中自带的一些方法,例如max、min等冲突,为了避免这些麻烦大家就约定俗成的都使用这种方法。
ndarray-多维数组对象
Numpy的核心特征就是N-维数组对——ndarray.
为什么用ndarray?
需求:
已知若干家跨国公司的市值(美元),将其换算为人民币
按照Python当中的方法
第一种:是将所有的美元通过for循环依次迭代出来,然后用每个公司的市值乘以汇率
第二种:通过map方法和lambda函数映射
这些方法相对来说也挺好用的,但是再来看通过ndarray对象是如何计算的

通过ndarray这个多维数组对象可以让这些批量计算变得更加简单,当然这只它其中一种优势,接下来就通过具体的操作来发现。
创建ndarray对象
np.array()
ndarray是一个多维数组列表
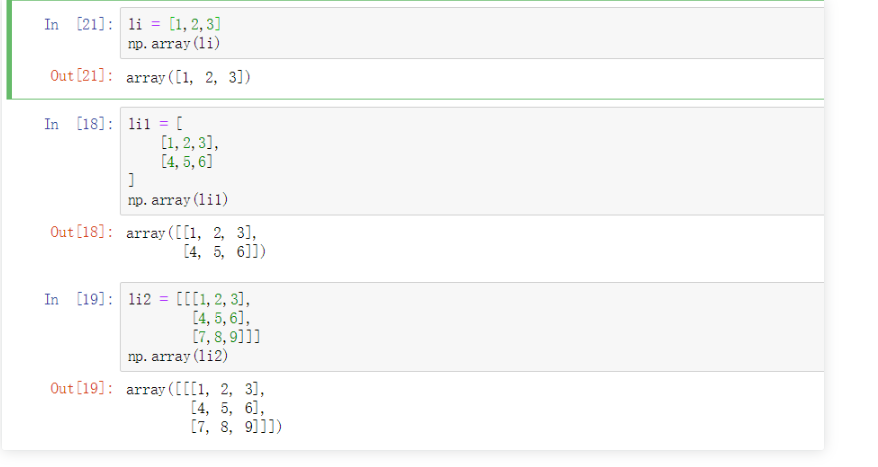
有的人可能会说了,这个数组跟Python中的列表很像啊,它和列表有什么区别呢?
- 数组对象内的元素类型必须相同
- 数组大小不可修改
常用属性
属性 描述
T 数组的转置
dtype 数组的数据类型
size 数组元素的个数
ndim 数组的维数
shape 数组的维度大小(以元组的形式)
T:转置 li1 = [ [1,2,3], [4,5,6] ] a = np.array(li1) a.T 执行结果: array([[1, 4], [2, 5], [3, 6]]) 就相当于是将行变成列,列变成行,它也是一个比较常用的方法
数据类型
类型 描述
布尔型 bool_
整型 int_ int8 int16 int32 int 64
无符号整型 uint8 uint16 uint32 uint64
浮点型 float_ float16 float32 float64
复数型 complex_ complex64 complex128
int32只能表示(-2**31,2**31-1),因为它只有32个位,只能表示2**32个数
无符号整型:
只能用来存正数,不能用来存负数
补充:
astype()方法可以修改数组的数据类型
ndarray创建
方法 描述
array() 将列表转换为数组,可选择显式指定dtype
arange() range的numpy版,支持浮点数
linspace() 类似arange(),第三个参数为数组长度
zeros() 根据指定形状和dtype创建全0数组
ones() 根据指定形状和dtype创建全1数组
empty() 根据指定形状和dtype创建空数组(随机值)
eye() 根据指定边长和dtype创建单位矩阵
1、arange(): np.arange(1.2,10,0.4) 执行结果: array([1.2, 1.6, 2. , 2.4, 2.8, 3.2, 3.6, 4. , 4.4, 4.8, 5.2, 5.6, 6. , 6.4, 6.8, 7.2, 7.6, 8. , 8.4, 8.8, 9.2, 9.6]) # 在进行数据分析的时候通常我们遇到小数的机会远远大于遇到整数的机会,这个方法与Python内置的range的使用方法一样 ----------------------------------------------------------------- 2、linspace() np.linspace(1,10,20) 执行结果: array([ 1. , 1.47368421, 1.94736842, 2.42105263, 2.89473684, 3.36842105, 3.84210526, 4.31578947, 4.78947368, 5.26315789, 5.73684211, 6.21052632, 6.68421053, 7.15789474, 7.63157895, 8.10526316, 8.57894737, 9.05263158, 9.52631579, 10. ]) # 这个方法与arange有一些区别,arange是顾头不顾尾,而这个方法是顾头又顾尾,在1到10之间生成的二十个数每个数字之间的距离相等的,前后两个数做减法肯定相等 ---------------------------------------------------------------- 3、zeros() np.zeros((3,4)) 执行结果: array([[0., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]]) # 会用0生成三行四列的一个多维数组 --------------------------------------------------------------------- 4、ones() np.ones((3,4)) 执行结果: array([[1., 1., 1., 1.], [1., 1., 1., 1.], [1., 1., 1., 1.]]) # 会用1生成三行四列的一个多维数组 ------------------------------------------------------------------------ 5、empty() np.empty(10) 执行结果: array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]) # 这个方法只申请内存,不给它赋值 ----------------------------------------------------------------------- 6、eye() np.eye(5) 执行结果: array([[1., 0., 0., 0., 0.], [0., 1., 0., 0., 0.], [0., 0., 1., 0., 0.], [0., 0., 0., 1., 0.], [0., 0., 0., 0., 1.]])
索引和切片
li1 = [ [1,2,3], [4,5,6] ] a = np.array(li1) a * 2 运行结果: array([[ 2, 4, 6], [ 8, 10, 12]])
索引
# 将一维数组变成二维数组 arr = np.arange(30).reshape(5,6) # 后面的参数6可以改为-1,相当于占位符,系统可以自动帮忙算几列 arr # 将二维变一维 arr.reshape(30) # 索引使用方法 array([[ 0, 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10, 11], [12, 13, 14, 15, 16, 17], [18, 19, 20, 21, 22, 23], [24, 25, 26, 27, 28, 29]]) 现在有这样一组数据,需求:找到20 列表写法:arr[3][2] 数组写法:arr[3,2] # 中间通过逗号隔开就可以了
切片
arr数组 array([[ 0, 1, 2, 3, 4, 5], [ 6, 7, 8, 9, 10, 11], [12, 13, 14, 15, 16, 17], [18, 19, 20, 21, 22, 23], [24, 25, 26, 27, 28, 29]]) arr[1:4,1:4] # 切片方式 执行结果: array([[ 7, 8, 9], [13, 14, 15], [19, 20, 21]])
切片不会拷贝,直接使用的
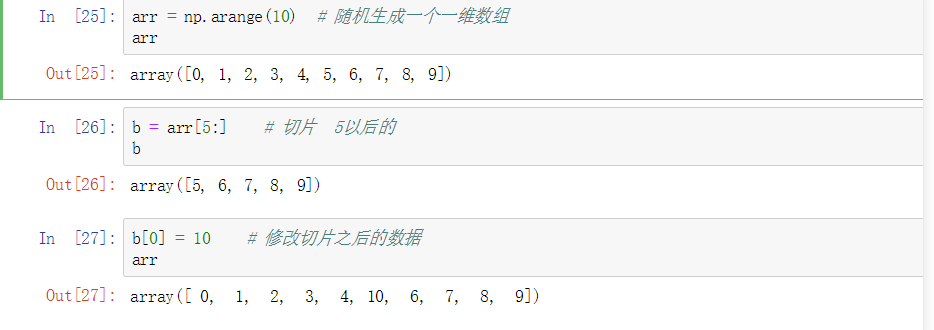
布尔型索引
li = [random.randint(1,10) for _ in range(30)] a = np.array(li) a[a>5] 执行结果: array([10, 7, 7, 9, 7, 9, 10, 9, 6, 8, 7, 6]) ---------------------------------------------- 原理: a>5会对a中的每一个元素进行判断,返回一个布尔数组 a > 5的运行结果: array([False, True, False, True, True, False, True, False, False, False, False, False, False, False, False, True, False, True, False, False, True, True, True, True, True, False, False, False, False, True]) ---------------------------------------------- 布尔型索引:将同样大小的布尔数组传进索引,会返回一个有True对应位置的元素的数组
花式索引
就是数组里面套数组,然后里面的数组存放索引。
通用函数
能对数组中所有元素同时进行运算的函数就是通用函数。
一元函数
函数 功能
abs 分别是计算整数和浮点数的绝对值
sqrt 计算各元素的平方根
square 计算各元素的平方
exp 计算各元素的指数e**x
log 计算自然对数
sign 计算各元素的正负号
cell 计算各元素的ceiling值
floor 计算各元素floor值,即小于等于该值的最大整数
rint 计算各元素的值四舍五入到最接近的整数,保留dtype
modf 将数组的小数部分和整数部分以两个独立数组的形式返回,与Python的divmod方法类似
isnan 计算各元素的正负号
isinf 表示那些元素是无穷的布尔型数组
cos,min,tan 普通型和双曲型三角函数
二元函数
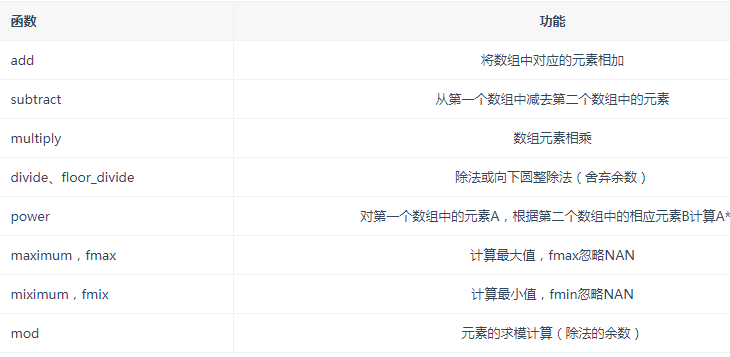
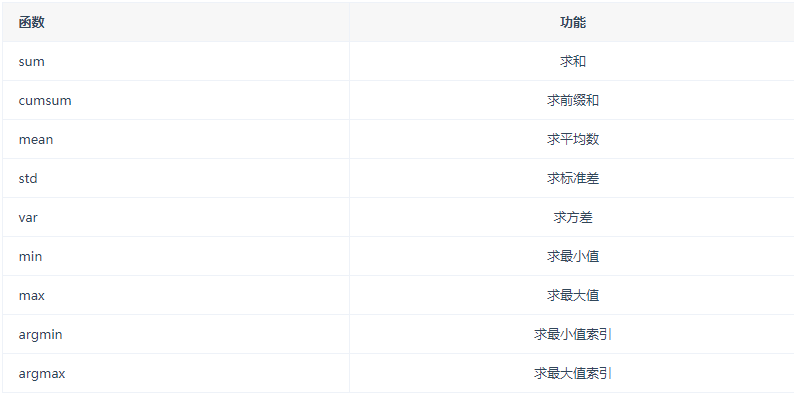
数学统计方法
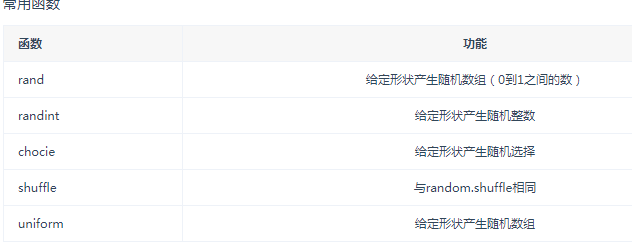
随机数
随机数生成函数在np.random的子包当中