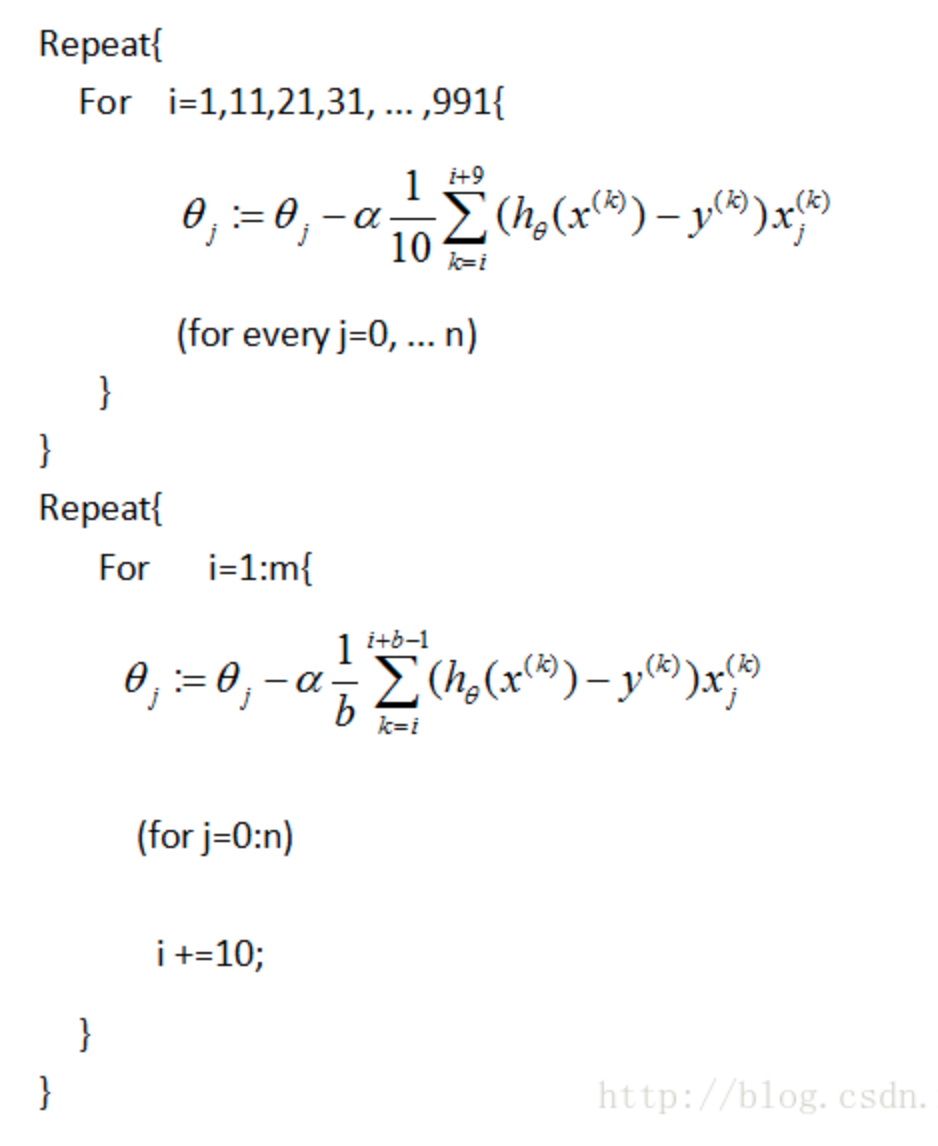吴恩达机器学习笔记 —— 2 单变量线性回归

第一章讲述了基本的机器学习的概念以及分类，这里从单变量的线性回归入手，吴恩达讲解了机器学习中的几个重要因素，如模型、损失函数、优化方法等

更多内容参考 机器学习&深度学习

首先以房价预测入手：

房子的面积	每平米的房价
2104	460
1416	232
1534	315
852	178

其中：

• m 为 样本的数量
• x 是样本的特征
• y 是预测的值
• ((x,y)) 就是一条样本数据
• (({ x }^{ (i) },{ y }^{ (i) })) 是第i条样本

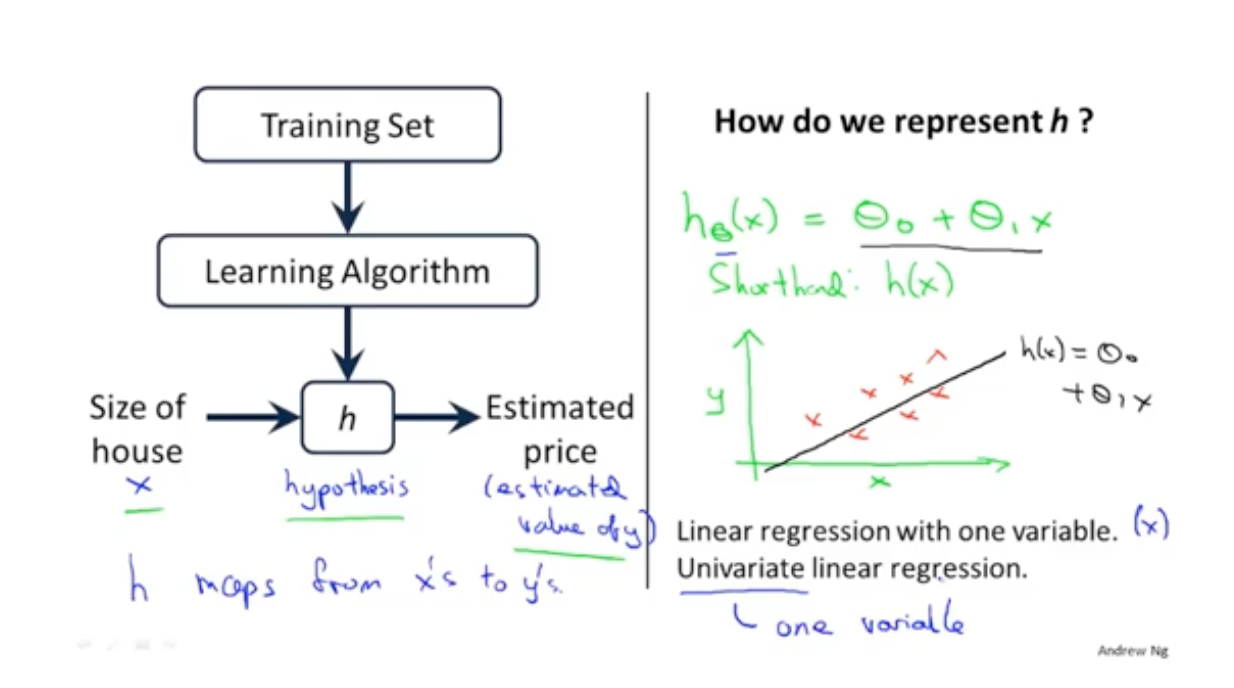
机器学习的过程就是通过上面的例子学习一个模型，当再次有数据x进来的时候，能给出对应的y值

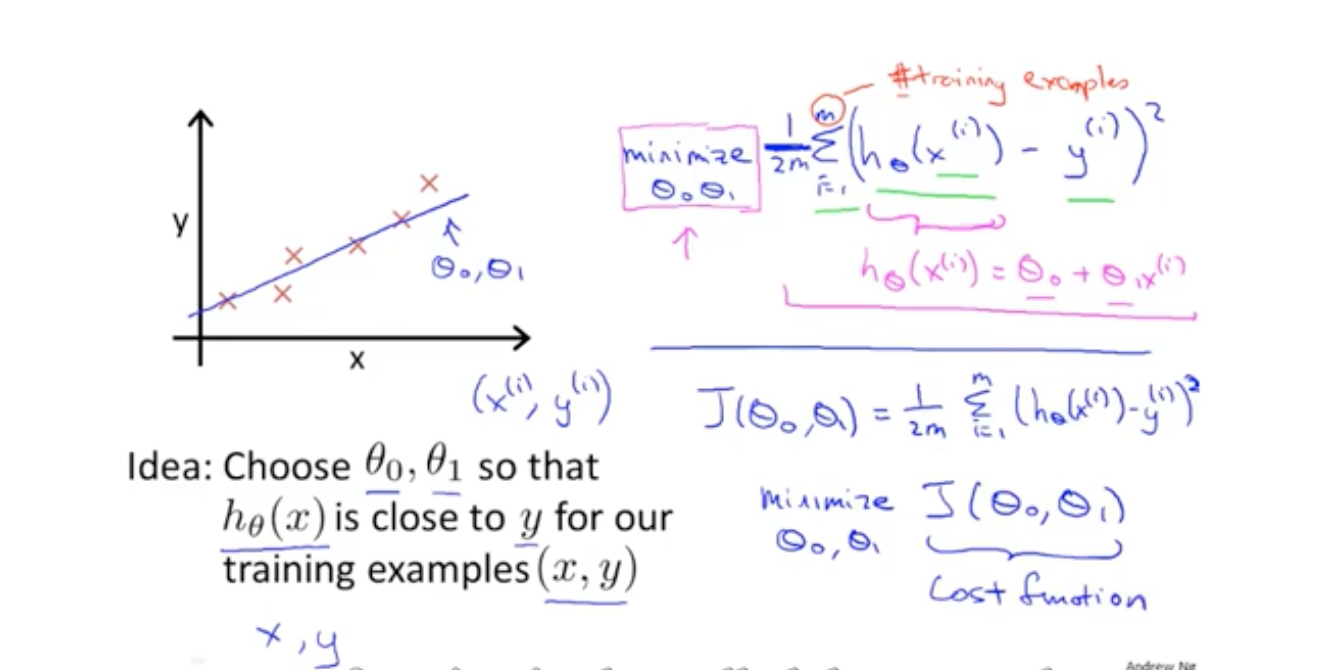
代价函数就是真实的值与我们预测的值之间的偏差，由于偏差有可能正，有可能负，因此使用均方差来表示。

不同的参数对应的损失值是不一样的，最终机器学习的目的就是寻找这个损失之最低的方法。



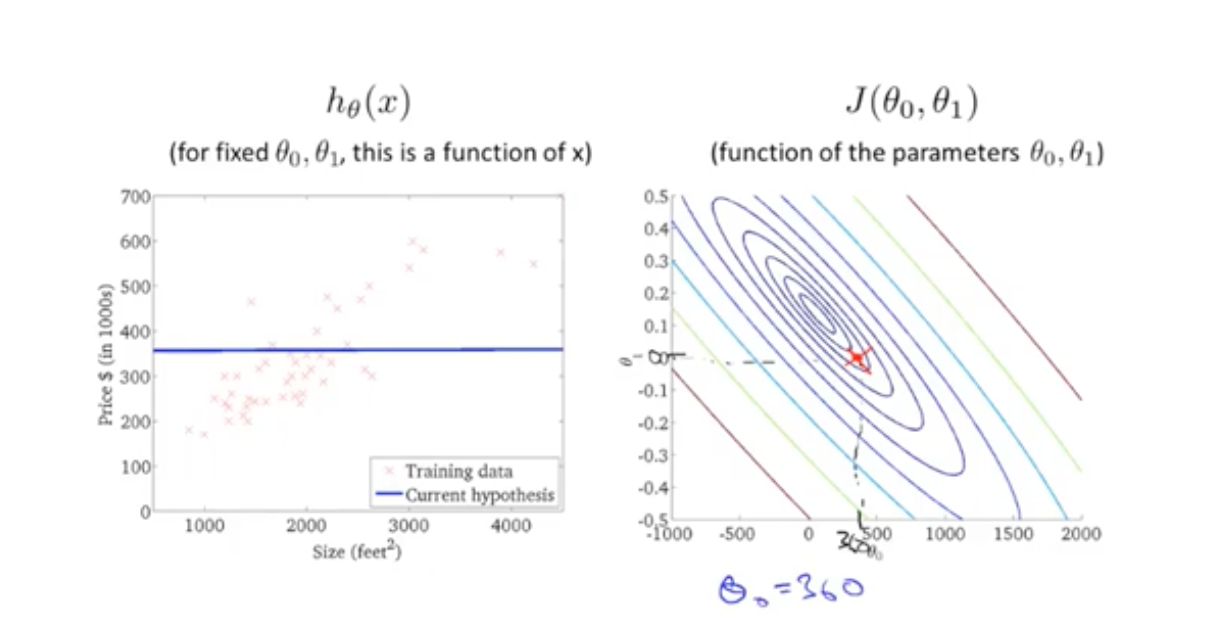
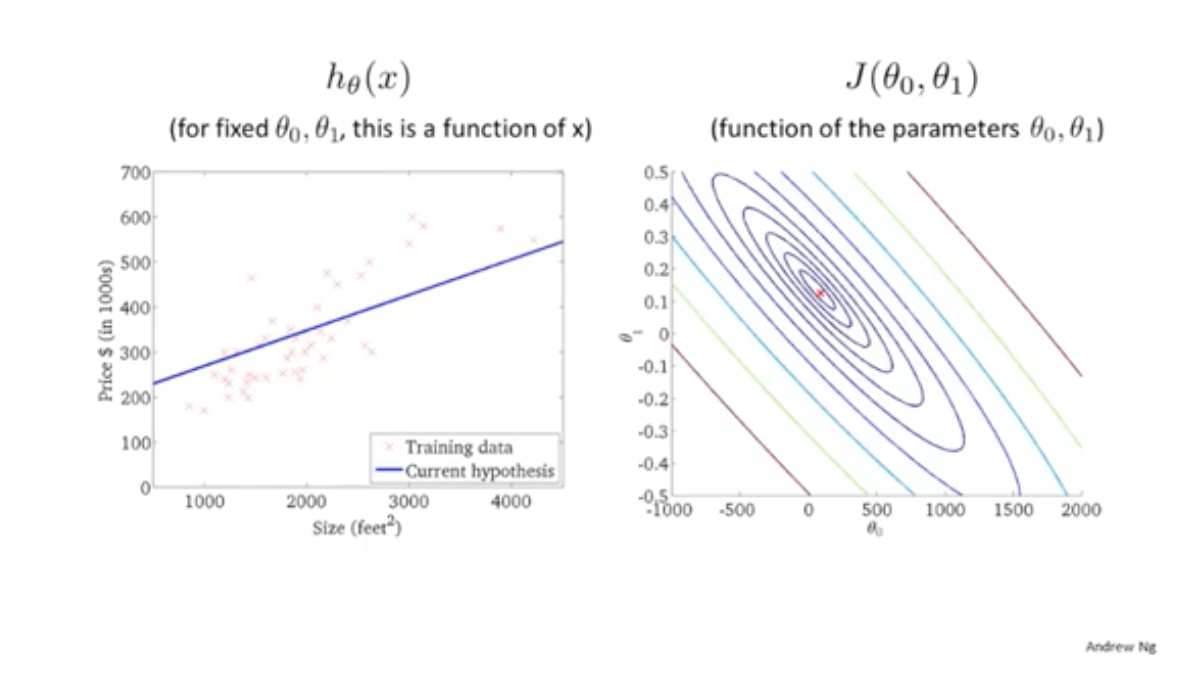
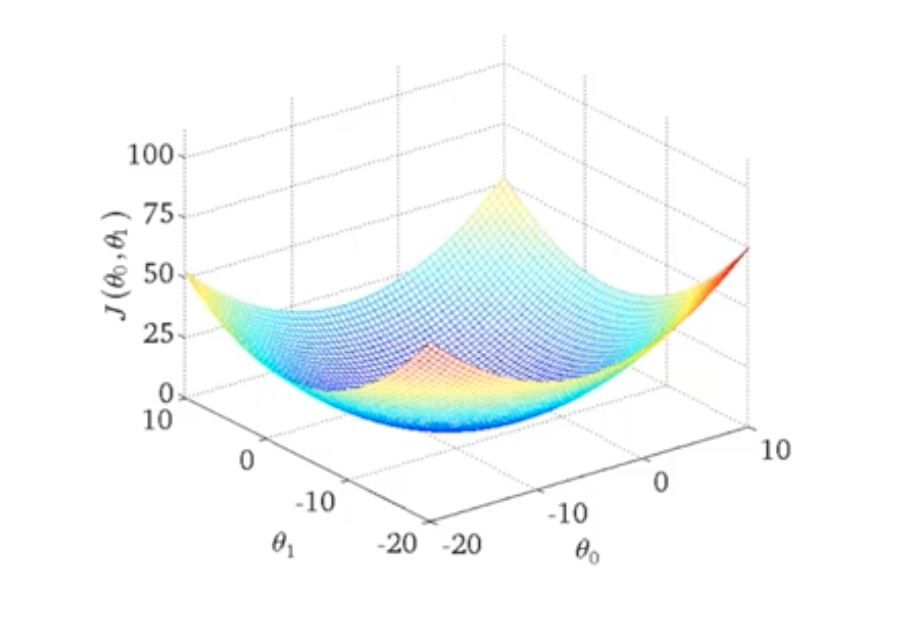
在二维特征下，可以看成一个关于损失函数的等高线图。同一个线圈，损失函数的值是相同的。在越来越靠近中心点时，可以看到预测的直线越来越贴近样本值。证明在等高线最中心的位置（最低点），损失值是最小的。

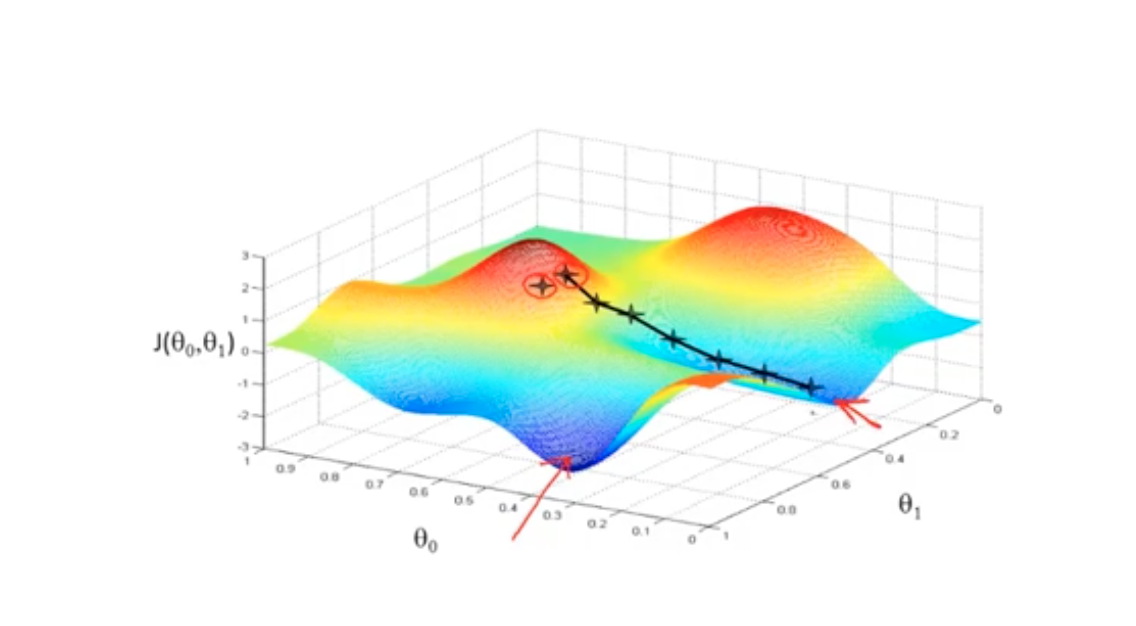
梯度下降可能找到是一个局部最优解，而不是全局最优解。

1. 参数随着每次迭代而改变
2. α是学习率，可以控制每次步长的变化
3. 每次改变的长度是基于偏导求解的
4. 在修改参数时，应该统一计算修改的值，再统一进行调整

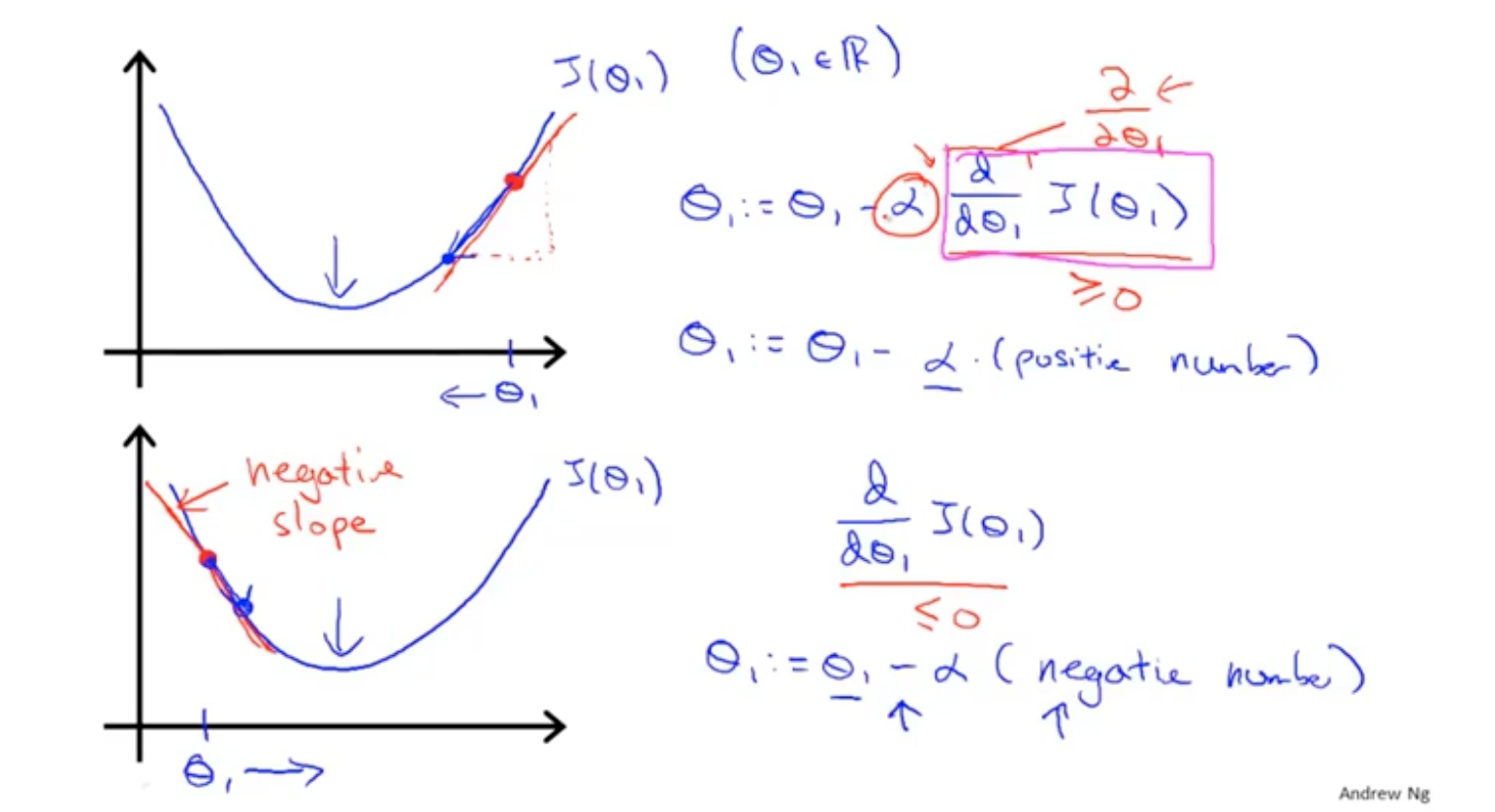
无论在最低点的哪一侧，公式都能保证θ是朝着最低点的位置在变化。

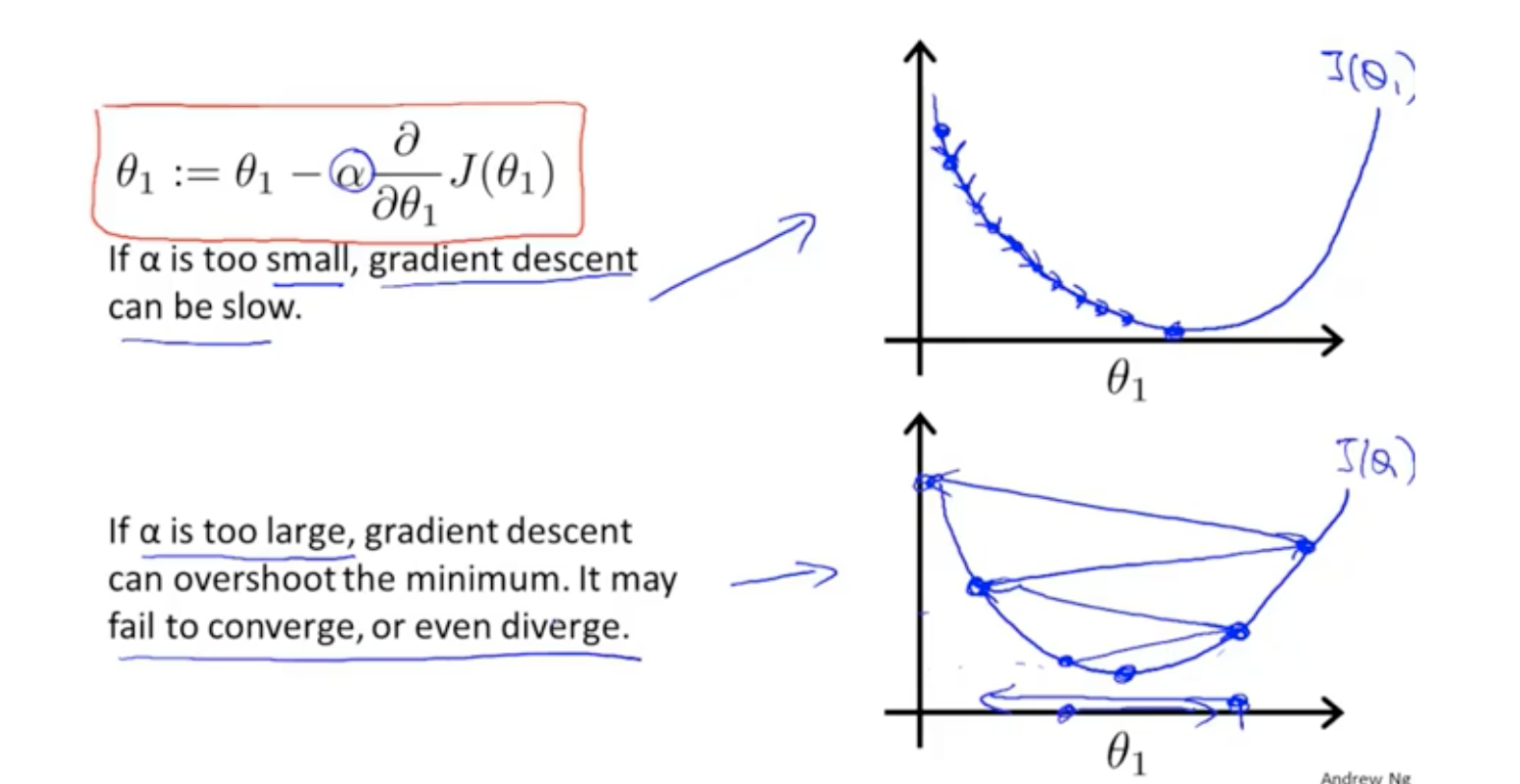
学习率的大小决定了能否快速找到最优解。

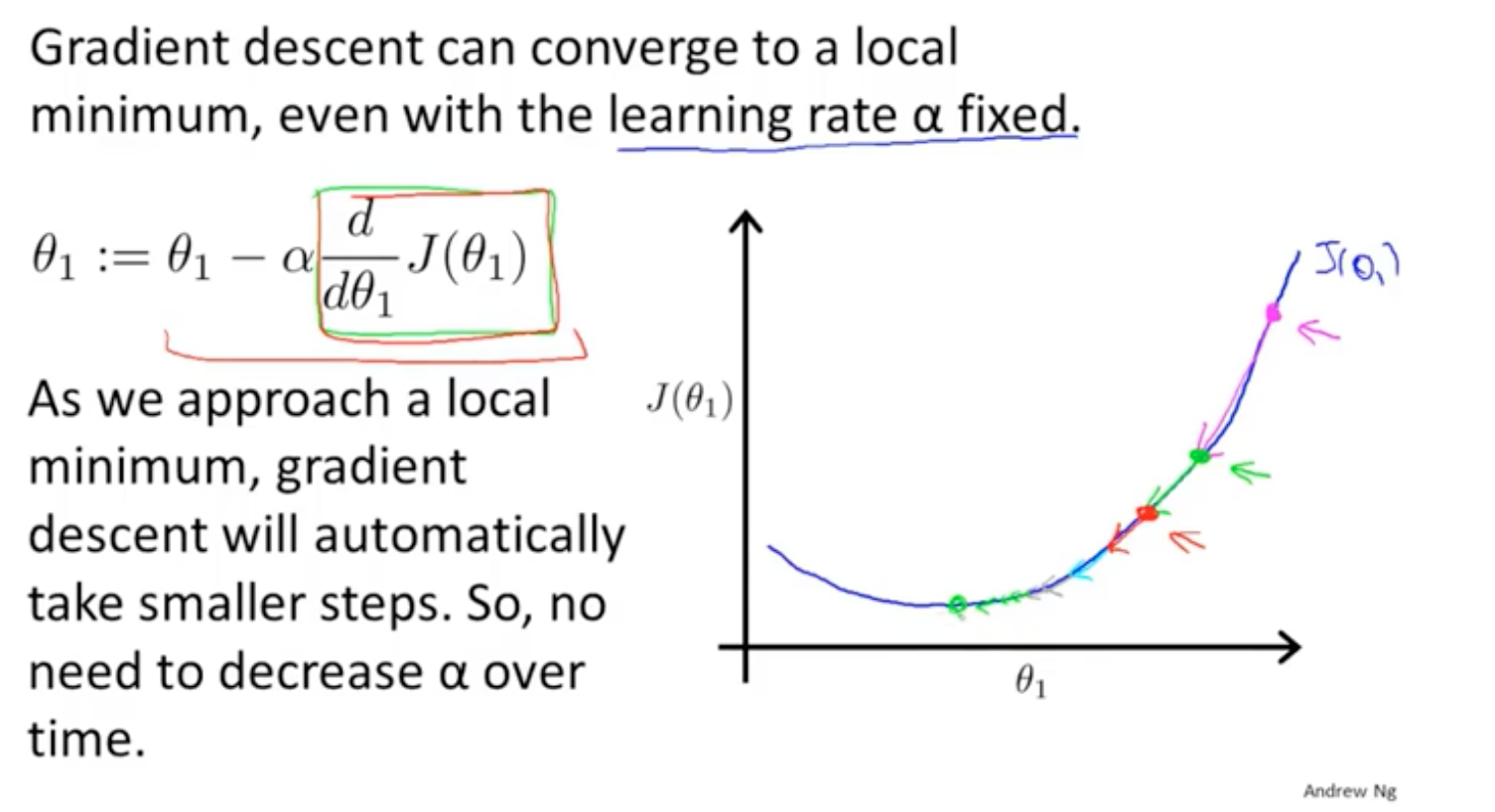
随机梯度下降在靠近最优解的时候，步长将会变得越来越小。

线性回归中，梯度下降是上面这样的。

针对优化的方法，有batch梯度下降、随机梯度下降、mini-batch梯度下降等等

batch梯度下降

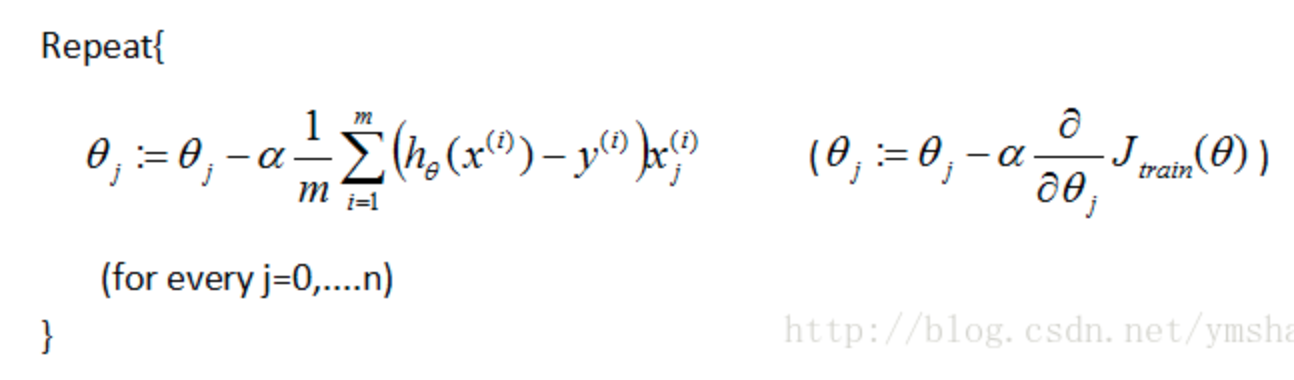
随机梯度下降

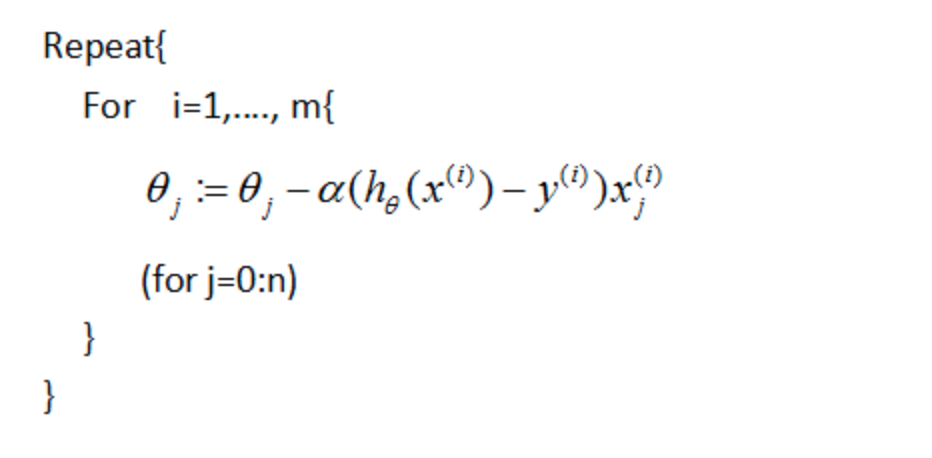
mini-batch梯度下降

参考：https://blog.csdn.net/ymshan92/article/details/54790657