ecjtu-summer training #9

A Robot

Description

The Robot Moving Institute is using a robot in their local store to transport different items. Of course the robot should spend only the minimum time necessary when travelling from one place in the store to another. The robot can move only along a straight line (track). All tracks form a rectangular grid. Neighbouring tracks are one meter apart. The store is a rectangle N x M meters and it is entirely covered by this grid. The distance of the track closest to the side of the store is exactly one meter. The robot has a circular shape with diameter equal to 1.6 meter. The track goes through the center of the robot. The robot always faces north, south, west or east. The tracks are in the south-north and in the west-east directions. The robot can move only in the direction it faces. The direction in which it faces can be changed at each track crossing. Initially the robot stands at a track crossing. The obstacles in the store are formed from pieces occupying 1m x 1m on the ground. Each obstacle is within a 1 x 1 square formed by the tracks. The movement of the robot is controlled by two commands. These commands are GO and TURN.
The GO command has one integer parameter n in {1,2,3}. After receiving this command the robot moves n meters in the direction it faces.

The TURN command has one parameter which is either left or right. After receiving this command the robot changes its orientation by 90o in the direction indicated by the parameter.

The execution of each command lasts one second.

Help researchers of RMI to write a program which will determine the minimal time in which the robot can move from a given starting point to a given destination.

Input

The input consists of blocks of lines. The first line of each block contains two integers M <= 50 and N <= 50 separated by one space. In each of the next M lines there are N numbers one or zero separated by one space. One represents obstacles and zero represents empty squares. (The tracks are between the squares.) The block is terminated by a line containing four positive integers B1 B2 E1 E2 each followed by one space and the word indicating the orientation of the robot at the starting point. B1, B2 are the coordinates of the square in the north-west corner of which the robot is placed (starting point). E1, E2 are the coordinates of square to the north-west corner of which the robot should move (destination point). The orientation of the robot when it has reached the destination point is not prescribed. We use (row, column)-type coordinates, i.e. the coordinates of the upper left (the most north-west) square in the store are 0,0 and the lower right (the most south-east) square are M - 1, N - 1. The orientation is given by the words north or west or south or east. The last block contains only one line with N = 0 and M = 0.

Output

The output contains one line for each block except the last block in the input. The lines are in the order corresponding to the blocks in the input. The line contains minimal number of seconds in which the robot can reach the destination point from the starting point. If there does not exist any path from the starting point to the destination point the line will contain -1.

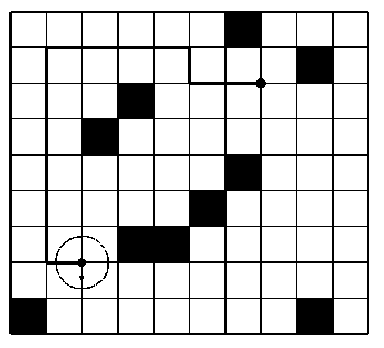
Sample Input

9 10
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 1 0
7 2 2 7 south
0 0

Sample Output

12

一个机器人，执行每一个命令耗时1，有两个命令，1、向左向右转90度。2、向前走1、2或3步，求从起点到终点的最少耗时时间。

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
#define ll long long
using namespace std;
const int MAX = 55;
const int INF = 1<<30;
const int dir[4][2]{{-1,0},{0,1},{1,0},{0,-1}};

struct Nod{
    int x;
    int y;
    int t;
    int d;
    bool operator < (const Nod &a) const{
        return t > a.t;
    }
};
int g[MAX][MAX], n, m, mark[MAX][MAX][4];
int bfs(int bx, int by, int ex, int ey, int f) {
    priority_queue<Nod> que;
    Nod nod;
    mark[bx][by][f] = 0;
    que.push((Nod){bx,by,0,f});
    while(!que.empty()) {
        nod = que.top();
        que.pop();
        int x = nod.x, y = nod.y;
        if(x == ex && y == ey) return nod.t;
        int d = nod.d;
        if(mark[x][y][(d+1)%4] == -1 || mark[x][y][(d+1)%4] > nod.t + 1){
            mark[x][y][(d+1)%4] = nod.t+1;
            que.push((Nod){x,y,nod.t+1,(d+1)%4});
        }
        if(mark[x][y][(d-1+4)%4] == -1 || mark[x][y][(d-1+4)%4] > nod.t + 1){
            mark[x][y][(d-1+4)%4] = nod.t + 1;
            que.push((Nod){x,y,nod.t+1,(d-1+4)%4});
        }
        int nx = x, ny = y;
        for(int i = 1; i <= 3; i ++) {
            nx += dir[d][0];
            ny += dir[d][1];
            if(nx <= 0 || nx >= m || ny <= 0 || ny >= n)break;
            if(g[nx][ny] == 1 || g[nx-1][ny] == 1 || g[nx][ny-1] == 1 || g[nx-1][ny-1] == 1) break;
            ///上行必须要用四个判断，因为机器人是在线上的，而障碍物是块，比如在(7,2)这个点，判断这个点
            //是否可以走，就要判断(7,2),(7,1),(6,1),(6,2)这个四个点有没有块
            if(mark[nx][ny][d] == -1 || mark[nx][ny][d] > nod.t+1){
                mark[nx][ny][d] = nod.t+1;
                que.push((Nod){nx,ny,nod.t+1,d});
            }
        }
    }
    return -1;
}
int main() {
    int bx, by, ex, ey, d, ans;
    char str[20];
    while(scanf("%d%d",&m,&n)&&(n+m)) {
        for(int i = 0; i < m; i ++) {
            for(int j = 0; j < n; j ++) {
                scanf("%d",&g[i][j]);
            }
        }
        scanf("%d %d %d %d %s",&bx,&by,&ex,&ey,str);
        if(str[0] == 'n') d = 0;
        else if(str[0] == 'e') d = 1;
        else if(str[0] == 's') d = 2;
        else if(str[0] == 'w') d = 3;
        memset(mark,-1,sizeof(mark));
        ans = bfs(bx,by,ex,ey,d);
        printf("%d
",ans);
    }
    return 0;
}

B 湫湫系列故事——消灭兔子

Problem Description

　　湫湫减肥
　　越减越肥！
　　
　　最近，减肥失败的湫湫为发泄心中郁闷，在玩一个消灭免子的游戏。
　　游戏规则很简单，用箭杀死免子即可。
　　箭是一种消耗品，已知有M种不同类型的箭可以选择，并且每种箭都会对兔子造成伤害，对应的伤害值分别为Di（1 <= i <= M），每种箭需要一定的QQ币购买。
　　假设每种箭只能使用一次，每只免子也只能被射一次，请计算要消灭地图上的所有兔子最少需要的QQ币。

 

Input

输入数据有多组，每组数据有四行；
第一行有两个整数N，M（1 <= N, M <= 100000），分别表示兔子的个数和箭的种类；
第二行有N个正整数，分别表示兔子的血量Bi（1 <= i <= N）；
第三行有M个正整数，表示每把箭所能造成的伤害值Di（1 <= i <= M）；
第四行有M个正整数，表示每把箭需要花费的QQ币Pi（1 <= i <= M）。

特别说明：
1、当箭的伤害值大于等于兔子的血量时，就能将兔子杀死；
2、血量Bi，箭的伤害值Di，箭的价格Pi，均小于等于100000。

 

Output

如果不能杀死所有兔子，请输出”No”，否则，请输出最少的QQ币数，每组输出一行。

 

Sample Input

3 3

1 2 3

2 3 4

1 2 3

3 4

1 2 3

1 2 3 4

1 2 3 1

 

Sample Output

6

4

 

优先队列+贪心。一开始贪心思路出错，然后有想了个办法，可以用线段树做，每个箭的伤害当成一个区间坐标，QB当成它的值，

兔子的血从高往低排序，每次射一个兔子时选它的血当 l，区间的最大值当r，去找[l,r]这个区间的最小值然后把它标记为INF就行了。

可惜没有写出来，而这种思路正好可以用优先队列做。糊涂了，绕了这么多弯。

 

#include <iostream>
#include <stdio.h>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
#define ll long long
const int MAX = 100010;
int b[MAX];
struct Nod{
    int d,q;
}nod[MAX];
bool cmp(Nod a, Nod b) {
    return a.d < b.d;
}
int main() {
    int n,m;
    while(scanf("%d%d",&n,&m)!=EOF){
        for(int i = 0; i < n; i ++) scanf("%d",&b[i]);
        for(int i = 0; i < m; i ++) scanf("%d",&nod[i].d);
        for(int i = 0; i < m; i ++) scanf("%d",&nod[i].q);
        if(n > m) {
            printf("No
");
            continue;
        }
        sort(b,b+n);
        sort(nod,nod+m,cmp);
        priority_queue<int, vector<int>, greater<int> >que;
        int k = m-1;
        bool flag = true;
        ll ans = 0;
        for(int i = n-1; i >= 0; i --) {
            while(k >= 0 && nod[k].d >= b[i]){
                que.push(nod[k].q);
                k--;
            }
            if(que.empty()){
                flag = false;
                break;
            }
            ans += que.top();
            que.pop();
        }
        if(flag)printf("%lld
",ans);
        else printf("No
");
    }
    return 0;
}

C. Timofey and a tree

昨天的原题。

#include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
const int N = 1e5+10;
int x[N], y[N], h[N], c[N];
int main() {
    int n;
    scanf("%d",&n);
    for(int i = 1; i < n; i ++) scanf("%d %d",&x[i],&y[i]);
    for(int i = 1; i <= n; i ++) scanf("%d",&c[i]);
    int m = 0;
    for(int i = 1; i < n; i ++) {
        if(c[x[i]] != c[y[i]]){
            m++;
            h[x[i]]++;h[y[i]]++;
        }
    }
    for(int i = 1; i <= n; i ++){
        if(h[i] == m){
            return 0*printf("YES
%d
",i);
        }
    }
    printf("NO
");
    return 0;
}

D Collecting Bugs

Description

Ivan is fond of collecting. Unlike other people who collect post stamps, coins or other material stuff, he collects software bugs. When Ivan gets a new program, he classifies all possible bugs into n categories. Each day he discovers exactly one bug in the program and adds information about it and its category into a spreadsheet. When he finds bugs in all bug categories, he calls the program disgusting, publishes this spreadsheet on his home page, and forgets completely about the program.
Two companies, Macrosoft and Microhard are in tight competition. Microhard wants to decrease sales of one Macrosoft program. They hire Ivan to prove that the program in question is disgusting. However, Ivan has a complicated problem. This new program has s subcomponents, and finding bugs of all types in each subcomponent would take too long before the target could be reached. So Ivan and Microhard agreed to use a simpler criteria --- Ivan should find at least one bug in each subsystem and at least one bug of each category.
Macrosoft knows about these plans and it wants to estimate the time that is required for Ivan to call its program disgusting. It's important because the company releases a new version soon, so it can correct its plans and release it quicker. Nobody would be interested in Ivan's opinion about the reliability of the obsolete version.
A bug found in the program can be of any category with equal probability. Similarly, the bug can be found in any given subsystem with equal probability. Any particular bug cannot belong to two different categories or happen simultaneously in two different subsystems. The number of bugs in the program is almost infinite, so the probability of finding a new bug of some category in some subsystem does not reduce after finding any number of bugs of that category in that subsystem.
Find an average time (in days of Ivan's work) required to name the program disgusting.

Input

Input file contains two integer numbers, n and s (0 < n, s <= 1 000).

Output

Output the expectation of the Ivan's working days needed to call the program disgusting, accurate to 4 digits after the decimal point.

Sample Input

1 2

Sample Output

3.0000


题意：有n种bug和s种子系统，bug的数量是无限的，一个程序员每天都可以发现一个bug，现在求的是发现n中bug并存在
于s个子系统中的平均天数（期望）。题意有点难懂，读了好几遍了。
假设dp[i][j]表示已经发现了i种bug并存在于j个子系统中（注意是已经发现了），那么dp[n][s] 就是 0了。
从dp[i][j]经过一天会出现4中情况
1、dp[i+1][j+1],出现一个新的bug并存在一个新的子系统中，概率是(n-i)*(s-j)/(n*s)
2、dp[i][j+1],在一个子系统中出现一个bug，不过这个bug种类是之前出现过的，概率是(s-j)*i/(n*s)
3、dp[i+1][j],出现一个新的bug，但是在子系统的已经出现过了，概率是(n-i)*j/(n*s)
4、dp[i][j],在已经发现过的bug中发现一个bug，概率是i*j/(n*s)
然后根据E(aA+bB+cC+dD+...)=aEA+bEB+....;//a,b,c,d...表示概率,A,B,C...表示状态
所以dp[i][j]=p1*dp[i+1][j+1]+p2*dp[i+1][j]+p3*dp[i][j+1]+p4*dp[i][j]+1;//dp[i][j]表示的就是到达状态i,j的期望 
=>dp[i][j]=(p1*dp[i+1][j+1]+p2*dp[i+1][j]+p3*dp[i][j+1]+1)/(1-p4);

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#define ll long long
using namespace std;
const int MAX = 1010;
double dp[MAX][MAX];
int main() {
    int n,s;
    while(scanf("%d%d",&n,&s)!=EOF){
        memset(dp,0,sizeof(dp));
        for(int i = n; i >= 0; i --) {
            for(int j = s; j >= 0; j --) {
                if(i == n && j == s)continue;
                dp[i][j] = (i*(s-j)*dp[i][j+1]+(n-i)*j*dp[i+1][j]+(n-i)*(s-j)*dp[i+1][j+1]+n*s)/(n*s-i*j);
            }
        }
        //printf("+++
");
        printf("%.4f
",dp[0][0]);
    }
    return 0;
}

E An old Stone Game

Description

There is an old stone game.At the beginning of the game the player picks n(1<=n<=50000) piles of stones in a line. The goal is to merge the stones in one pile observing the following rules:
At each step of the game,the player can merge two adjoining piles to a new pile.The score is the number of stones in the new pile.
You are to write a program to determine the minimum of the total score.

Input

The input contains several test cases. The first line of each test case contains an integer n, denoting the number of piles. The following n integers describe the number of stones in each pile at the beginning of the game.
The last test case is followed by one zero.

Output

For each test case output the answer on a single line.You may assume the answer will not exceed 1000000000.

Sample Input

1
100
3
3 4 3
4
1 1 1 1
0

Sample Output

0
17
8

一条线上有n堆石头，每堆石头都有一个数量，可以合并相邻的两堆石头，每次合并会产生一个值，是两堆石头的总数，求合并成一堆石头时，总值是多少。
GarsiaWachs算法。做法就是，比如序列是a[n],从前往后寻找，找到k满足a[k]<a[k+2],然后合并a[k]和a[k+1]，替换为新值s,然后从k往前寻找，
找到第一个大于s的数，并把s插到那个数的后面。

#include <iostream>
#include <stdio.h>
#include <string.h>
#define ll long long
using namespace std;
const int MAX = 5e4+5;
int num, n, a[MAX];
ll ans;
void dfs(int now) {
    int j;
    int temp = a[now-1] + a[now];
    ans += (ll)temp;
    for(int i = now; i < num -1; i ++) a[i] = a[i+1];
    num--;
    for(j = now-1; j > 0&& a[j-1] < temp; j --) a[j] = a[j-1];
    a[j] = temp;
    while(j >= 2 && a[j-2] <= a[j]){
        int d = num - j;
        dfs(j-1);
        j = num-d;
    }
}
int main() {
    while(scanf("%d",&n)&&n){
        for(int i = 0; i < n; i ++) scanf("%d",&a[i]);
        num = 1;
        ans = 0;
        for(int i = 1; i < n; i ++) {
            a[num++] = a[i];
            while(num >= 3 && a[num-3] <= a[num-1]) dfs(num-2);
        }
        while(num > 1) dfs(num-1);
        printf("%lld
",ans);    
    }
    return 0;
}