斐波那契数列的定义如下:
F(0) = 0
F(1) = 1
F(n) = F(n - 1) + F(n - 2) (n >= 2)
(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...)
给出n,求F(n),由于结果很大,输出F(n) % 1000000009的结果即可。
Input
输入1个数n(1 <= n <= 10^18)。
Output
输出F(n) % 1000000009的结果。
Input示例
11
Output示例
89
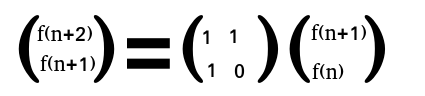
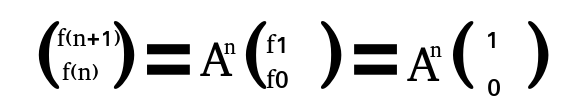
所以求出A^n就可以求出f(n)了。
1 #include <iostream> 2 #include <stdio.h> 3 #include <string.h> 4 #include <vector> 5 #define ll long long 6 using namespace std; 7 typedef vector<ll> vec; 8 typedef vector<vec> mat; 9 const ll Mod = 1000000009; 10 11 mat mul(mat &A, mat &B) { 12 mat C(A.size(), vec(B[0].size())); 13 for(int i = 0; i < A.size(); i ++) { 14 for(int k = 0; k < B.size(); k ++) { 15 for(int j = 0; j < B[0].size(); j ++) { 16 C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % Mod; 17 } 18 } 19 } 20 return C; 21 } 22 mat pow(mat A, ll n) { 23 mat B(A.size(), vec(A.size())); 24 for(int i = 0; i < A.size(); i ++) { 25 B[i][i] = 1; 26 } 27 while(n > 0) { 28 if(n&1) B = mul(B,A); 29 A = mul(A,A); 30 n >>= 1; 31 } 32 return B; 33 } 34 int main() { 35 ll n; 36 cin >> n; 37 mat A(2, vec(2)); 38 A[0][0] = 1; A[0][1] = 1; 39 A[1][0] = 1; A[1][1] = 0; 40 A = pow(A, n); 41 printf("%lld ",A[1][0]); 42 return 0; 43 }