Top-model Izabella participates in the competition. She wants to impress judges and show her mathematical skills.
Her problem is following: for given string, consisting of only 0 and 1, tell if it's possible to remove some digits in such a way, that remaining number is a representation of some positive integer, divisible by 64, in the binary numerical system.
In the only line given a non-empty binary string s with length up to 100.
Print «yes» (without quotes) if it's possible to remove digits required way and «no» otherwise.
100010001
yes
100
no
In the first test case, you can get string 1 000 000 after removing two ones which is a representation of number 64 in the binary numerical system.
You can read more about binary numeral system representation here: https://en.wikipedia.org/wiki/Binary_system
1后面有6个0就yes
1 #include <bits/stdc++.h> 2 using namespace std; 3 char str[110]; 4 int main() { 5 int flag = 0, ans = 0; 6 cin >> str; 7 for(int i = 0; str[i]; i ++) { 8 if(str[i] == '1') flag = 1; 9 if(str[i] == '0' && flag) ans++; 10 } 11 if(ans >= 6) printf("yes "); 12 else printf("no "); 13 return 0; 14 }
Absent-minded Masha got set of n cubes for her birthday.
At each of 6 faces of each cube, there is exactly one digit from 0 to 9. Masha became interested what is the largest natural x such she can make using her new cubes all integers from 1 to x.
To make a number Masha can rotate her cubes and put them in a row. After that, she looks at upper faces of cubes from left to right and reads the number.
The number can't contain leading zeros. It's not required to use all cubes to build a number.
Pay attention: Masha can't make digit 6 from digit 9 and vice-versa using cube rotations.
In first line integer n is given (1 ≤ n ≤ 3) — the number of cubes, Masha got for her birthday.
Each of next n lines contains 6 integers aij (0 ≤ aij ≤ 9) — number on j-th face of i-th cube.
Print single integer — maximum number x such Masha can make any integers from 1 to x using her cubes or 0 if Masha can't make even 1.
3
0 1 2 3 4 5
6 7 8 9 0 1
2 3 4 5 6 7
87
3
0 1 3 5 6 8
1 2 4 5 7 8
2 3 4 6 7 9
98
In the first test case, Masha can build all numbers from 1 to 87, but she can't make 88 because there are no two cubes with digit 8.
求1-x x中的每一位是可以从给定的每组数据中找到。
直接写。
1 #include <bits/stdc++.h> 2 using namespace std; 3 set<int> st[4]; 4 bool ok(int x) { 5 int cnt = 0, b[4]; 6 while(x) { 7 b[cnt++] = x%10; 8 x /= 10; 9 } 10 switch(cnt){ 11 case 1: 12 for(int i = 1; i <= 3; i ++) { 13 if(st[i].count(b[0])) return true; 14 } 15 return false; 16 break; 17 case 2: 18 for(int i = 1; i <= 3; i ++) { 19 for(int j = 1; j <= 3; j ++) { 20 if(i == j) continue; 21 if(st[i].count(b[0]) && st[j].count(b[1])) return true; 22 } 23 } 24 return false; 25 break; 26 case 3: 27 for(int i = 1; i <= 3; i ++) { 28 for(int j = 1; j <= 3; j ++) { 29 for(int k = 1; k <= 3; k ++) { 30 if(i == j || i == k || i == k) continue; 31 if(st[i].count(b[0]) && st[j].count(b[1]) && st[k].count(b[2])) return true; 32 } 33 } 34 } 35 return false; 36 break; 37 } 38 } 39 int main() { 40 int n, x; 41 cin >> n; 42 for(int i = 1; i <= n; i ++) { 43 for(int j = 1; j <= 6; j ++) { 44 cin >> x; 45 st[i].insert(x); 46 } 47 } 48 for(int i = 1; ; i ++) { 49 if(!ok(i)) return 0*printf("%d ",i-1); 50 } 51 return 0; 52 }
During the breaks between competitions, top-model Izabella tries to develop herself and not to be bored. For example, now she tries to solve Rubik's cube 2x2x2.
It's too hard to learn to solve Rubik's cube instantly, so she learns to understand if it's possible to solve the cube in some state using 90-degrees rotation of one face of the cube in any direction.
To check her answers she wants to use a program which will for some state of cube tell if it's possible to solve it using one rotation, described above.
Cube is called solved if for each face of cube all squares on it has the same color.
In first line given a sequence of 24 integers ai (1 ≤ ai ≤ 6), where ai denotes color of i-th square. There are exactly 4 occurrences of all colors in this sequence.
Print «YES» (without quotes) if it's possible to solve cube using one rotation and «NO» (without quotes) otherwise.
2 5 4 6 1 3 6 2 5 5 1 2 3 5 3 1 1 2 4 6 6 4 3 4
NO
5 3 5 3 2 5 2 5 6 2 6 2 4 4 4 4 1 1 1 1 6 3 6 3
YES
In first test case cube looks like this:
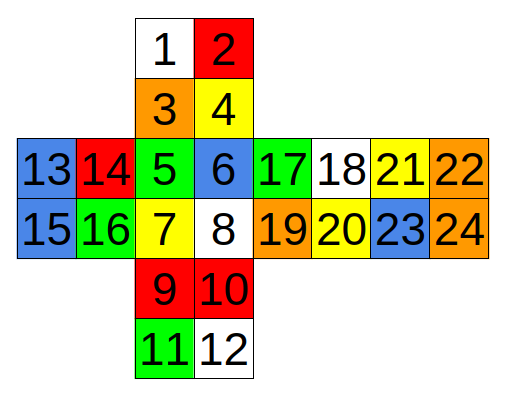
In second test case cube looks like this:
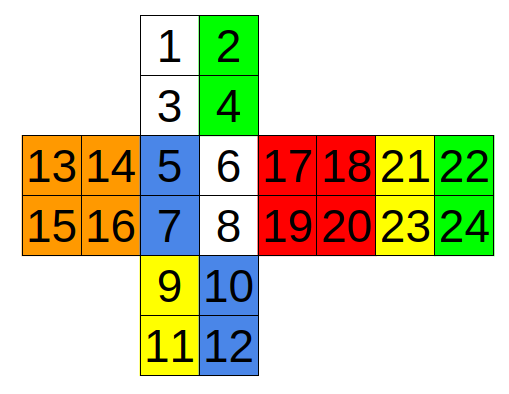
It's possible to solve cube by rotating face with squares with numbers 13, 14, 15, 16.
给定的二阶魔方中 是否可以旋转90还原魔方。6中情况。都用if判断下了 就是麻烦了点、
1 #include <bits/stdc++.h> 2 using namespace std; 3 int a[25]; 4 5 bool ok1() { 6 if(a[13]==a[14]&&a[14]==a[15]&&a[15]==a[16]&&a[17]==a[18]&&a[18]==a[19]&&a[19]==a[20]) { 7 if(a[21]==a[23]&&a[23]==a[9]&&a[9]==a[11]&&a[22]==a[24]&&a[24]==a[2]&&a[2]==a[4]) { 8 if(a[1]==a[3]&&a[3]==a[6]&&a[6]==a[8]&&a[5]==a[7]&&a[7]==a[10]&&a[10]==a[12]) { 9 return true; 10 } 11 } 12 } 13 return false; 14 } 15 bool ok2() { 16 if(a[13]==a[14]&&a[14]==a[15]&&a[15]==a[16]&&a[17]==a[18]&&a[18]==a[19]&&a[19]==a[20]) { 17 if(a[6]==a[8]&&a[8]==a[9]&&a[9]==a[11]&&a[10]==a[12]&&a[12]==a[22]&&a[22]==a[24]) { 18 if(a[21]==a[23]&&a[23]==a[1]&&a[1]==a[3]&&a[2]==a[4]&&a[4]==a[5]&&a[5]==a[7]) { 19 return true; 20 } 21 } 22 } 23 return false; 24 } 25 bool ok3() { 26 if(a[1]==a[2]&&a[2]==a[3]&&a[3]==a[4]&&a[9]==a[10]&&a[10]==a[11]&&a[11]==a[12]) { 27 if(a[13]==a[14]&&a[14]==a[7]&&a[7]==a[8]&&a[5]==a[6]&&a[6]==a[19]&&a[19]==a[20]) { 28 if(a[17]==a[18]&&a[18]==a[23]&&a[23]==a[24]&&a[21]==a[22]&&a[22]==a[15]&&a[15]==a[16]) { 29 return true; 30 } 31 } 32 } 33 return false; 34 } 35 bool ok4() { 36 if(a[1]==a[2]&&a[2]==a[3]&&a[3]==a[4]&&a[9]==a[10]&&a[10]==a[11]&&a[11]==a[12]) { 37 if(a[13]==a[14]&&a[14]==a[23]&&a[23]==a[24]&&a[5]==a[6]&&a[6]==a[15]&&a[15]==a[16]) { 38 if(a[17]==a[18]&&a[18]==a[7]&&a[7]==a[8]&&a[21]==a[22]&&a[22]==a[19]&&a[19]==a[20]) { 39 return true; 40 } 41 } 42 } 43 return false; 44 } 45 bool ok5() { 46 if(a[5]==a[6]&&a[6]==a[7]&&a[7]==a[8]&&a[21]==a[22]&&a[22]==a[23]&&a[23]==a[24]) { 47 if(a[1]==a[2]&&a[2]==a[17]&&a[17]==a[19]&&a[18]==a[20]&&a[20]==a[9]&&a[9]==a[10]) { 48 if(a[11]==a[12]&&a[12]==a[14]&&a[14]==a[16]&&a[13]==a[15]&&a[15]==a[3]&&a[3]==a[4]) { 49 return true; 50 } 51 } 52 } 53 return false; 54 } 55 bool ok6() { 56 if(a[5]==a[6]&&a[6]==a[7]&&a[7]==a[8]&&a[21]==a[22]&&a[22]==a[23]&&a[23]==a[24]) { 57 if(a[1]==a[2]&&a[2]==a[14]&&a[14]==a[16]&&a[18]==a[20]&&a[20]==a[3]&&a[3]==a[4]) { 58 if(a[11]==a[12]&&a[12]==a[17]&&a[17]==a[19]&&a[13]==a[15]&&a[15]==a[9]&&a[9]==a[10]) { 59 return true; 60 } 61 } 62 } 63 return false; 64 } 65 bool ok() { 66 if(ok1() || ok2() || ok3() || ok4() || ok5() || ok6()) return true; 67 return false; 68 } 69 int main() { 70 for(int i = 1; i <= 24; i ++) cin >> a[i]; 71 if(ok()) printf("YES "); 72 else printf("NO "); 73 return 0; 74 }