2017-2018 ACM-ICPC, Asia Daejeon Regional Contest

C

有n个节点和m边条，求一条最长的路径，该路径(c1,c2,c3...cn)满足 不出现重复的节点，c_i 和c_i+1是邻居节点，且 c_i 的邻居节点数量小于c_i+1的邻居节点数量。

记忆DFS遍历，每次递归计算的值都保存在数组里，这样复杂度相当于O(m)

#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define ll long long
using namespace std;
const int N = 1e5+10;
vector<int> vs[N];
int MAX, ans[N];
int dfs(int v) {
    if(ans[v]!=0) return ans[v];
    int cnt = 0;
    for(auto u : vs[v]) {
        if(vs[u].size() > vs[v].size()) {
            cnt = max(cnt, dfs(u));
        }
    }
    ans[v] = cnt+1;
    return cnt+1;
}
int main() {
    int n, m, v, u;
    cin >> n >> m;
    for(int i = 1; i <= m; i ++) {
        cin >> v >> u;
        vs[v].push_back(u);
        vs[u].push_back(v);
    }
    for(int i = 0; i < n; i ++) {
        dfs(i);
        MAX = max(MAX, ans[i]);
    }
    cout << MAX << endl;
    return 0;
}

D

给定一个数字x，问一直使用x = f(x)这个函数是否可以将x变成1.

f(x) 的定义是对每一位数进行平方求和。签到题

#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define ll long long
using namespace std;
map<int,int> mp;
int f(int x) {
    int ans = 0;
    while(x) {
        int y = x%10;
        ans += y*y;
        x /= 10;
    }
    return ans;
}
int main() {
    int n;
    cin >> n;
    while(true) {
        n = f(n);
        if(n == 1) return 0*printf("HAPPY
");
        if(mp.count(n)) break;
        mp[n] = 1;
    }
    printf("UNHAPPY
");
    return 0;
}

F

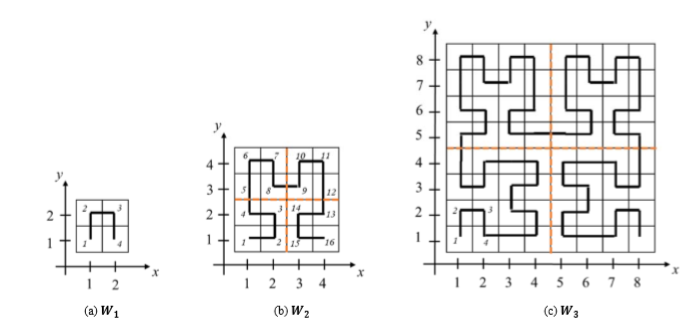
已知边长和走的步数，求当前的位置。

分而治之。对于当前边长为n的图，可以分为四份。

如果在左下角，顺时针旋转了90°，相当于x和y值交换下。

如果在右下角，逆时针旋转了90°，相当于x和y值交换下，对称看。

如果在左上角，y值加n/2。

如果在右上角，x值和y值都加n/2。

#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define ll long long
using namespace std;
const int N = 1e5+10;
struct Point{
    int x, y;
};
Point dfs(int n, int m) {
    Point a;
    if(n == 2) {
        if(m == 0) a.x = 1, a.y = 1;
        else if(m == 1) a.x = 1, a.y = 2;
        else if(m == 2) a.x = 2, a.y = 2;
        else if(m == 3) a.x = 2, a.y = 1;
        return a;
    }
    int ans = n*n/4;
    int cnt = m%ans;
    a = dfs(n/2, cnt);
    if(m < ans) {
        swap(a.x, a.y);
    } else if(m < 2*ans) {
        a.y += n/2;    
    } else if(m < 3*ans) {
        a.x += n/2;
        a.y += n/2;
    } else {
        int x = n+1-a.y;
        int y = n/2+1 - a.x;
        return (Point){x, y};
    }
    return a;
}

int main() {
    int n, m;
    cin >> n >> m;
    Point p = dfs(n, m-1);
    printf("%d %d
",p.x,p.y);
    return 0;
}

H

有两个字符串，只有三个字符，R(石头)、S(剪刀)和P(布)，求第二个在第一个在哪里开始比赛赢的数数最多，求数量。

12 4

RSPPSSSRRPPR

RRRR

第二个字符串从第4或第5位置开始可以赢3把，所以答案是3。

题目可以转成成从哪里开始，位置一一对应是相同的数量。将第二个字符串反转，使用fft套模板就出答案了。

主要是想到为什么对第二个字符进行反转，假设有两个字符串

1 2 3 456

RRRSSS

SSPR

1 2 3 4

RPSS

从第一个位置开始，一一对应是1+4,2+3,3+2,4+1，都是5 

从第二个位置开始，一一对于是2+4,3+3,4+2,5+1，都是6

这样就知道为什么反转了。只要对两个数组求卷积就行。

#include <iostream>
#include <algorithm>
#include <math.h>
#define INF 0x3f3f3f3f
#define ll long long
using namespace std;
const int N = 1e5+10;
char s1[N], s2[N];
const double PI = acos(-1.0);
struct complex {
    double r,i;
    complex(double _r = 0,double _i = 0) {
        r = _r; i = _i;
    }
    complex operator +(const complex &b) {
        return complex(r+b.r,i+b.i);
    }
    complex operator -(const complex &b) {
        return complex(r-b.r,i-b.i);
    }
    complex operator *(const complex &b) {
        return complex(r*b.r-i*b.i,r*b.i+i*b.r);
    }
};
void change(complex y[],int len) {
    int i,j,k;
    for(i = 1, j = len/2;i < len-1;i++) {
        if(i < j)swap(y[i],y[j]);
        k = len/2;
        while( j >= k) {
            j -= k;
            k /= 2;
        }
        if(j < k)j += k;
    }
}
void fft(complex y[],int len,int on) {
    change(y,len);
    for(int h = 2;h <= len;h <<= 1) {
        complex wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
        for(int j = 0;j < len;j += h) {
            complex w(1,0);
            for(int k = j;k < j+h/2;k++) {
                complex u = y[k];
                complex t = w*y[k+h/2];
                y[k] = u+t;
                y[k+h/2] = u-t;
                w = w*wn;
            }
        }
    }
    if(on == -1)
        for(int i = 0;i < len;i++)
            y[i].r /= len;
}

const int MAXN = 400040;
complex x1[MAXN], x2[MAXN];
int a[MAXN/4], n, m;
ll num[MAXN], ans[MAXN];
void slove(char ch) {
    int len = 1;
    while(len < 2*n || len < 2*m)len <<= 1;
    for(int i = 0;i < n;i++)
        x1[i] = complex(s1[i]==ch,0);
    for(int i = n;i < len;i++)
        x1[i] = complex(0,0);
    for(int i = 0;i < m;i++)
        x2[i] = complex(s2[i]==ch,0);
    for(int i = m;i < len;i++)
        x2[i] = complex(0,0);
    fft(x1,len,1);
    fft(x2,len,1);
    for(int i = 0;i < len;i++)
        x1[i] = x1[i]*x2[i];
    fft(x1,len,-1);
    for(int i = 0;i < len;i++)
        num[i] = (long long)(x1[i].r+0.5);
       for(int i = 0; i < len; i ++) 
           ans[i] += num[i];
}
int main() {
    cin >> n >> m;
    cin >> s1 >> s2;
    for(int i = 0; i < n; i ++) {
        if(s1[i] == 'R') s1[i] = 'P';
        else if(s1[i] == 'P') s1[i] = 'S';
        else if(s1[i] == 'S') s1[i] = 'R';
    }
    for(int i = 0; i < m/2; i ++) swap(s2[i], s2[m-i-1]);
    slove('R');
    slove('S');
    slove('P');
    ll MAX = 0;
    for(int i = m-1; i < n+m-1; i ++) MAX = max(MAX, ans[i]);
    cout << MAX << endl;
    return 0;
}