作者：桂。
时间：2017-05-06 08:39:37
链接：http://www.cnblogs.com/xingshansi/p/6815772.html
前言
还是李航的《统计学习方法》，主要是决策树的内容，主要包括ID3、C4.5以及对应的剪枝方法。内容为自己的学习记录，可能读起来会前言不搭后语。
一、决策树概念
决策就是选择：
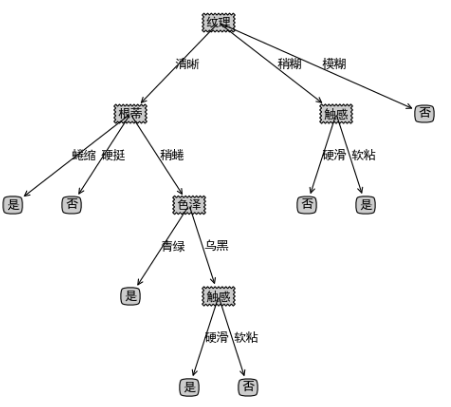
二、特征选择
根据决策树可以看出，根蒂、触感、色泽等都是特征，就像生活中很多事情要处理，不能同时兼顾，一些人给出了坐标轴的思路：
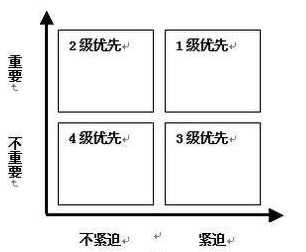
这也是一个决策树，并给出了感性的评价准则，从而决定了特征（待办事项）的先后顺序。特征的选择也依赖一定的准则，只不过不再是感性而是可以量化的，两种常用的准则分别是：信息增益、信息增益比，信息增益对应ID3算法，信息增益比队医C4.5算法。
三、决策树基本算法
A-ID3算法
首先给出熵的定义，X是一个取值有效的离散随机变量，其概率密度：
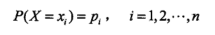
对应的熵：
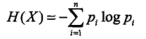
熵衡量的是不确定性，越不确定信息量就越大。
在给出变量Y在给定X时的条件熵：
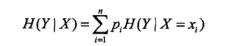
这就引出了信息增益的概念：
想一想：原始的信息量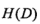
，减去基于先验知识A的信息量
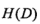，得到的就是信息增益。比如一开始选工作一片茫然，工作的信息量就非常大，一旦确定了所学的专业（A），很多人考虑的工作面就窄了。这个缩小的工作面就是信息增益，如果A是自己的身高呢，工作面缩小的可能小，如果A是家庭、所学专业，工作面缩小的就大一些，可见不同特征（A）的重要程度不同，它的直接体现就是信息增益。
信息增益的求解算法：
利用求解的信息增益，也就是重要程度，先做重要事情，这个时候特征就有了不同的优先级，决策树也就一步步构建出来了。
基于信息增益的ID3算法：
B-C4.5算法
C4.5是基于信息增益比，为什么要引入信息增益比呢？
原因：如果一个特征，决定的选择分支很多（如上文图中的纹理：3个），有些决定的相对较少（如触感：2个），这个差别有的更大，即使影响较小，但由于波及类别多，显得信息增益大，这是不合理的。因此希望对它进行一个的约束。
回顾一下谱聚类的思路：
直接图割的话，准则函数：
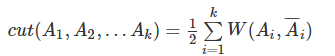图割中也有最小割的问题：
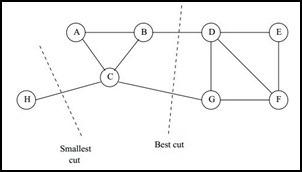
一个自然的想法就是，类似为了防止过拟合而添加正则项一样，可以添加新的限定，这就是谱聚类的思想。但限定并不唯一指定：
如RatioCut:
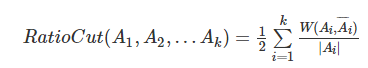
NCut:
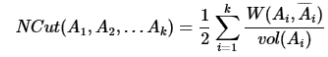
类似的，只要增加一个类别多的反向约束即可，这是信息增益比的出发点，具体定义：
其中
，HA(D)就是上面公式的H（D）.特征决定的选择越多，对应的熵就越大，从而形成了反向约束。
从而引出C4.5算法：
C-树的剪枝
首先看一看决策树整体的熵：
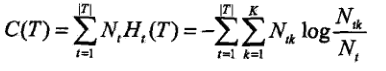
其中树T的叶节点个数为|T|。t是树T的叶节点，该叶节点有
个样本点，其中k类的样本点有
个，如果感觉这个公式莫名其妙，展开来看一看：
其中
是常数，乘不乘都不影响最终结果。对于离散随机变量X求均值，一般就是p*X可能取值，再求和。上面的C（T）其实就是不同节点熵的均值呀。为了防止过拟合，就是防止叶节点过多，添加约束项：
这就完成了剪枝的准则函数。给出具体实现思路：
对应的效果类似这样：
参考：
李航《统计学习方法》